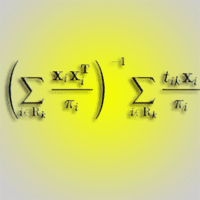
Design-based methodological advances to support national forest inventories: a review of recent proposals
iForest - Biogeosciences and Forestry, Volume 8, Issue 1, Pages 6-11 (2015)
doi: https://doi.org/10.3832/ifor1239-007
Published: Jun 18, 2014 - Copyright © 2015 SISEF
Review Papers
Abstract
The aim of this paper is to give an overview of some recent proposals to support national forest inventories. The reviewed literature is strictly of design- based nature, i.e., uncertainty only stems from the sampling scheme actually adopted in the survey, rather than being assumed or modeled as in model- based approaches. National forest inventories are viewed as two-phase sample surveys to estimate at the same occasion the extent of the continuous population of points constituting the forest cover and the total of a forest attribute (e.g., volume or biomass) in the discrete population of trees for several forest types and/or administrative districts. The first phase is performed from remote sensing imagery while the second phase is performed on the field, possibly adopting the information acquired in the first phase as auxiliary information. A novel methodology is adopted based on Monte Carlo integration methods, which leads to a very general estimation strategy. Some recent proposals are considered in which remote sensing information acquired in the first phase is used to assess some physical characteristics of non-forest resources, such as woodlots, tree-rows and isolated trees outside the forest without additional field work. Finally, a new proposal is discussed in which canopy height from laser scanning is adopted as auxiliary information to recover missing data occurring when some sampled points cannot be reached because of hazardous terrain.
Keywords
Two-phase Strategies, Aerial Information, Non-forest Resources, Missing Data, LiDAR, Calibration Weighting
Introduction
The analysis of forest ecology and the wise management of forest resources requires accurate monitoring of forestlands at regular time intervals. In turn, the monitoring process involves sample surveys to estimate extents and standing volumes for a wide set of forest types and districts. These surveys are usually referred to as forest inventories ([9], [10]).
The early forest inventories were performed toward the end of 15th century in the form of censuses of oaks in the Republic of Venice ([6]). Occasional censuses of forest resources were also performed in Tuscany till the 18th century. During the 20th century, methods for inventorying forests were rapidly improved and the possibility of reducing costs by adopting sampling methods were recognized. The first forest inventory at country level, henceforth referred to as national forest inventory (NFI), was performed in Finland from 1922 to 1924 and from now repeated every ten years. The first Italian NFI was performed from 1982 to 1985, while the second started in 2003 and concluded at the end of 2006 (see ⇒ http:// www.infc.it).
This paper provides a review of some recent methodological contributions to support NFIs. All the reviewed articles are of design-based nature, in the sense that uncertainty only stems from the sampling scheme adopted to perform the inventory. As Särndal et al. ([39]) point out “Design-based inference is objective; nobody can challenge that the sample was really selected according to the given sampling design. The probability distribution associated with the design is real, not modelled or assumed”.
In the next section NFIs are viewed as two-phase sample surveys to estimate at the same occasion the extent of the continuous population of points constituting the forest cover and the total of a forest attribute (e.g., volume or biomass) in the discrete population of trees for several forest types and/or administrative districts. Usually, NFIs are performed using an intensive first phase which is carried out on satellite imagery or aerial photos and a second phase which is carried out by ground inspections, possibly adopting the information acquired in the first phase as auxiliary information. A novel methodology is adopted based on Monte Carlo integration methods ([22], [29]), which leads to a very general estimation strategy valid for any second-phase sampling scheme. In section 3, some recent proposal are considered in which the aerial information acquired in the first NFI phase is exploited to investigate non forest resources, such as woodlots, tree-rows and isolated trees outside the forest. In section 4 a new proposal is discussed in which canopy height from laser scanning is adopted as auxiliary information to account for missing data occurring when some sampled points cannot be reached by forest crews because of hazardous terrain. Final remarks are given in section 5.
Two-phase inventories
Consider a delineated study area A partitioned into two land cover classes: forest and non forest. Denote by F ⊂ A the forest portion of A and by U the population of forest trees within F. Suppose that F is partitioned into K sub-portions F1, …, FK corresponding to K forest types (e.g., oak, pine, larch, etc.) or K spatial districts or combinations of the twos, in such a way that U is partitioned into K sub-populations U1, …, UK of trees within the K sub-portions.
Generally speaking, a forest inventory is a sampling strategy to estimate the extent of the k-th forest type/district (eqn. 1):
and the total of a forest attribute Y (e.g., volume, biomass, basal area, etc. - eqn. 2):
for each k = 1, …, K, where yk (p) is the indicator variable of the k-th forest type/category defined in the continuous population of points p ∈ A and is such that yk (p) = 1 if p ∈ A and yk (p) = 0 otherwise, while yj is the amount of Y corresponding to the j-th tree in the discrete population of trees U.
An essential requirement of any NFI is that extents and totals are estimated in the same survey, using the same aerial and field investigations.
First phase
Gregoire & Valentine ([22]) and Mandallaz ([29]) provide excellent introductory treatments on the issue of sampling discrete objects (forest trees in the present case) scattered over a region by means of plots or transects (plots in the present case) to estimate a total. The authors emphasize that these sampling strategies may be conveniently re-formulated as spatial strategies for sampling the continuous populations of points constituting the study area and estimating an integral within. Gregoire & Valentine ([22]) also provide a list of references from the early 1990s in which such a novel intuition was first developed. In this setting, the inventory issue of estimating both extents and totals is unified, because just like extents, the totals can be expressed as integrals over the study area. The difference between extents and totals is due to the variable to be recorded. As to extents, the survey variable is the indicator variable at the sampled point; as to totals, the survey variable is the whole amount of the forest attribute Y recorded for the trees lying within the plot of prefixed size and shape centred at the sampled point. Accordingly, in the first phase a unique spatial design for selecting points (from which plots are centred) suffices for both extent and total estimation. As pointed out by Gregoire & Valentine ([22]) and Mandallaz ([29]), in this framework estimation reduces to a two-dimensional Monte Carlo integration. Thus the key problem is how to effectively select the first-phase points to better perform integration.
Despite its simplicity, the completely random placement of N first-phase points, usually referred to as the uniform random sampling (URS), may lead to uneven coverage of the study area, because some parts of the area may be sparsely sampled whereas others are intensively sampled. To avoid the drawback, stratified or systematic schemes can be adopted. A stratified scheme, usually referred to as the tessellation stratified sampling (TSS) is performed as follows: the area A is covered by a region R ⊃ A of size R, constituted by N non-overlapping regular polygons of equal size R1, …, RN, and such that Ri ∩ A ≠ Ø for all i = 1, …, N. Then, for each polygon i, a point is randomly thrown within the polygon. Alternatively, a systematic scheme, usually referred to as the systematic grid sampling (SGS) can be used: in this case a point is randomly selected in one polygon (e.g., the first) and then repeated in the remaining N - 1. Most of the NFIs adopted the SGS scheme, while TSS has been recently applied in the last Italian NFI ([17]).
If each first-phase point is visited on the ground and the indicator variable of each type/district is recorded at the point, the first-phase Monte-Carlo integration estimator of Ak turns out to be (eqn. 3):
where fk = Nk / N and Nk is the number of sample points lying in Ak. Moreover, if for each first-phase point i lying in Ak a plot of fixed size a is delineated around the point, the attribute Y is recorded for all the trees in the plots, and the total tki is reckoned, the first-phase Monte-Carlo integration estimator of Tk turns out to be (eqn. 4):
where tki = 0 if i does not belong to Ak.
It is well-known from Monte Carlo integration ([22]) that (3) and (4) are unbiased estimators under URS, STS and SGS schemes. Moreover, under TSS and SGS, the variances of (3) and (4) decrease at a rate faster than N-1 ([3], [4], [5]), while URS provides variances decreasing with N-1. Accordingly, for large N, tessellation gives rise to relevant gains in precision with respect to URS.
It is worth noting that some edge effects may be present owing to forest trees positioned near the edge of the study region, which have inclusion probabilities smaller than the inner trees. A long list of correction methods has been proposed in order to avoid the negative bias induced by edge effects ([22]). Fortunately, in this framework, the TSS and SGS schemes, selecting first-phase points onto the enlarged region R, perform like the correction method usually referred to as the buffer method ([22]), i.e., the N points are allowed to fall outside the boundary of A, but within some larger region including A. For this reason, under TSS and SGS the presence of forest trees whose inclusion zone overlaps the boundary of the enlarged region R is likely to be negligible. Moreover, it should be noticed that in NFIs edges coincide with the country’s borderlines, i.e., mountains ridges, rivers, sea in which the presence of forest trees is very unlike to occur. Thus, if edge effects are ignored that should not entail detrimental effects on the bias of the estimators.
Second phase
Owing to costs and time involved, in real situations the N points selected in the first phase cannot be visited. Rather, only a portion of these points is selected in a second phase of sampling and is visited on the ground. Actually, the first-phase is only hypothetical and its treatment has the sole aim to lead to the estimators arising from the second phase.
Regarding the second phase, the collection of the N points selected in the first phase, say P, is usually partitioned into the sub-set PF of the NF points lying in the forest area F, and the sub-set P-PF of the remaining N-NF points lying outside. It is worth noting that the partition is performed by satellite imagery of aerial photos, without field work. Obviously, because the plots centered at the points of P-PF lie completely or partially outside forest, no or very few forest trees are likely to be found in these plots. Hence, it is customary to assume tki = 0 for any i ∈ P-PF, in such a way that the sampling effort can be completely devoted to PF.
The procedure of neglecting non-forest points in the second phase is adopted in most NFIs but it is not sufficiently focused in most familiar textbooks ([15], [40], [22], [29]). Even if the procedure is suitable from both theoretical and practical point of view because avoids the waste of sampling effort outside forest, it may provide downward bias in both extent and total estimation. Indeed, a point can be erroneously classified outside forest by aerial imaging. The issue of aerial classification errors is well known in forest inventorying, and first-phase errors can be accounted for in the second phase, achieving unbiased estimators of extent ([16]). However, if points classified as non-forest are excluded from the second phase of sampling, there is no way to account for those forest points erroneously classified as non-forest. This fact obviously entail underestimation of forest extents. At least to my knowledge, there is no inquiry or case study attempting to quantify how huge is the downward bias due to misclassification. To reduce misclassification effects, the first phase should include more auxiliary data sets as possible (e.g., maps, point clouds from airborne laser scanning, forest management plans etc.). If the aerial imagery is a high spatial resolution photographs, the non-forest areas should be quite easily distinguished from forest. In the same way, a plot centered at a point falling outside forest but near a forest stand, may contain a portion of forest trees which cannot be accounted because the point is excluded from the second phase. This fact obviously entail underestimation of totals. Some simulation studies ([28], [14]) have evidenced that the bias induced by the exclusion of non-forest points is negligible.
If non-forest points are discarded, denote by S ⊂ PF the second-phase sample of size n selected from PF by means of a fixed-size scheme inducing first- and second-order inclusion probabilities πi and πih (h > i ∈ PF). Suppose that πih > 0 for any h > i ∈ PF, in such a way that the second-phase variance can be unbiasedly estimated. Suppose also that no classification errors between forest and non-forest points occur, and that Pr(tki = 0 ∀ i ∈ P-PF) = 1. Using the double-expansion estimation ([39]), the two-phase estimators of extents and totals turn out to be (eqn. 5):
and (eqn. 6):
respectively, where Sk ⊂ S denotes the sub-sample of second-phase points lying in the k-th forest type/district.
Under the above-mentioned assumptions, estimators (5) and (6) turn out to be unbiased with sampling variances which in the case of (5) can be estimated by (eqn. 7):
and in the case of (6) by (eqn. 8):
Under TSS, (7) and (8) are proven to be conservative estimators of the actual variances. The conservative nature of (7) and (8) stems from TSS, owing to the independence among first-phase points ([45]). Nothing can be said about the properties of (5) and (6) under SGS. In this case the estimation of variance required more refined procedures ([35], [19]).
Most of NFIs involve two phases of sampling. Relevant examples are the NFIs of Canada ([21]), USA ([41]), the former Soviet Union ([20]), New Zealand ([42]), Romania and Switzerland ([44]). In the recent Italian NFI, three phases of sampling are adopted. In the Italian case, the second-phase points are visited to record the forest type in order to estimates extents, while the totals of forest attributes are estimated from a third-phase sample. The expressions of the third-phase estimators are obviously more cumbersome than those achieved in two phases. Details on third-phase estimators are given by Fattorini et al. ([17]).
The use of auxiliary information
As already pointed out, NFIs usually require estimates of extents and totals for several forest types, for several regions defined by political subdivisions, for other domains such as ownership categories and silvicultural types and for combinations of them. Practically speaking, thousands of estimates are produced as the output of a NFI. In this framework, statisticians have neither time nor resources to select ad hoc estimators for each survey variable. Therefore the only feasible way is to adopt linear estimators as those in equations (5) and (6), in which the weights attached to sample observations are constructed and applied to all variables and domains. Because these weights are derived from the sampling design, they do not effectively take advantage of the increasing availability of various inexpensive auxiliary data from remote sensing sources (e.g., photo-interpreted land cover class, location, elevation, slope and a sequence of thematic mapping spectral bands).
On the other hand, Opsomer et al. ([35]) emphasize the great opportunity to improve the accuracy of NFI estimates making use of auxiliary data derived from remote sensing sources That can be done by calibration procedures in which the original weights are adjusted, making them sum to totals of the auxiliary variables. Opsomer et al. ([35]) list a large number of techniques for adjusting sample weights. Most of them make use of super-population models understanding the relationships between key forestry variables and remotely sensed information. All of them adopt these models in the framework of model-assisted estimation, i.e., models are only used to determine the sample weights while the statistical properties of the resulting estimators are derived in a design-based framework from the scheme actually adopted to select the sample points. An application to Northern Utah Mountains data shows estimated efficiencies of the model-assisted estimators which vary from 1.3 to 2 with respect to the traditional FIA estimators ([35]).
Estimation of non-forest resources
During the FAO Expert Consultation on Global Forest Resources Assessment 2000 (Kotka, Finland 1996), the importance of trees outside forests (TOF) and the need for complete and detailed information about these stands were underlined for the first time. NFIs are currently requested to broaden their scopes to include the assessment of TOF attributes ([25], [26]). TOF include small woodlots, three rows, urban forests and isolated trees and play a basic role in biodiversity conservation and carbon sequestration. The main objective of TOF inventories is the estimation of totals and/or averages of some physical attribute of the units (e.g., woodlot size and tree-row length). Probably, an efficient solution would require the use of ad hoc sampling schemes for each of the target parameters. However, in order to save time and resources, it may be appealing to perform the estimation in the first-phase of NFIs, because most physical attributes can be recorded from the aerial information collected during the first inventory phase without any field work.
Quoting from Baffetta et al. ([2]), let W be the population of M woodlots, or trees rows or urban forests in the study area. Let w1, …, wM be the sizes of the M units and let yi be the value of a physical attribute of the j-th unit which can be recorded from aerial imagery. Suppose that the population total (eqn. 9):
and/or the population mean YW = TW / M are the parameters to be estimated. To this purpose, denote by G the set of distinct woodlots, tree rows or urban forests which contain at least one of the N first-phase points and let m be the (random) size of G. As proven by Baffetta et al. ([2]), under TSS the quantity (eqn. 10):
turns out to be an approximately unbiased estimators of TW. It is worth noting that (10) avoids the troublesome quantification of the portion of the selected units lying in adjacent quadrats, as would be requested by the genuine Horvitz-Thompson estimator. Moreover (eqn. 11):
is proven to be a conservative estimator for the variance of T(1)W. For yj invariably equal to 1, TW coincides with the population abundance M and (10) provides an abundance estimator, say M(1). Thus a very natural estimator of YW = TW / M is given by the ratio (eqn. 12):
which is approximately unbiased with variance estimator (eqn. 13):
The validity of these estimators is empirically checked by a simulation study ([2]). They are applied to estimate the average size and the abundance of the Italian urban forests from the sample of the 430 urban forests selected throughout Italy by the first-phase points of the last Italian NFI ([12]).
Regarding isolated trees, their abundance can be estimated from the aerial information acquired during NFIs, even if a further aerial sampling phase is necessary in this case. Baffetta et al. ([1]) propose the use of a second-phase in which the N first-phase points are partitioned into strata by using aerial imagery. Usually the strata coincide with land cover classes easily identifiable from the imagery. Then, a second-phase sample of points is selected from each strata by simple random sampling without replacement, a circle of fixed size is centered at the second-phase points and the number of isolated trees within the circle is counted once again from the aerial imagery. When the presence of isolated trees is more likely in some strata, these strata should be more intensively sampled. Moreover, because isolated trees are rare and widely scattered over territories, a suitable choice should be circles of about 100-200 m radius which are much larger than those usually adopted when surveying within forests (10-15 m radius). If W now denotes the population of M isolated trees over the study area, if P1, …, PL denote the L strata in which the population P of the N first-phase points is partitioned, N1, …, NL denote the stratum sizes, S1, …, SL denote the samples of points selected from each stratum and n1 , …, nL the sample sizes, the two-phase aerial estimator of M turns out to be ([1] - eqn. 14)
where b is the size of circles, pl = Nl / N, mi denotes the number of isolated trees aerially counted within the plot i and m l is the average of the mis for i ∈ Sl. The estimator (10) is unbiased with variance which can be unbiasedly estimated by (eqn. 15):
where sl2 is the sample variance of the mis for i ∈ Sl.
Obviously, if totals or averages of some biophysical attributes such as tree volume and biomass are of interest (rather than size or length), subsequent sampling phases must be performed on the field. Corona & Fattorini ([7]) propose the use of two-phase cluster sampling to survey tree rows, while Corona et al. ([11]) propose the use of sector sampling to survey woodlots. A third stratified sampling phase is suggested by Baffetta et al. ([1]) for field surveys of isolated trees.
Non-response treatment
Non-response is often a problem in NFIs. Non-response occurs for two main causes: (a) plots selected in the second phase are located in difficult terrains and cannot be reached by survey crews or, even if reached, the steep slope of the terrain does not allow the recording activities within; (b) plots selected in the second phase are inaccessible because of cultural prohibitions or because landowners deny field crews access. The reasons for non-response are not necessarily the same all over the world. In the USA, (a) is the primary reason for non-response. Procedures for treating non-response due to (a) are proposed by McRoberts ([30]) and are not treated here. This section deals with the problem of non-response adjustment when difficult terrains preclude access to plots or recording activities. This is especially relevant in those countries where forest areas are mainly located in mountainous and/or remote areas.
In this framework, non-response problems manly concern the estimation of totals, which involves the recording of forest attributes within the plots centered at second-phase points. On the other hand, as to the estimation of extents, in most situations the forest type at plot centers can be determined some distance away from the points or by means of high resolution aerial image, while the district in which plot centers fall can be even determined from the map.
A vast literature deals with the problem of non-response adjustment by means of several techniques, but most of them are judged unfeasible by Fattorini et al. ([18]) for environmental and forest surveys. Widely applied methods to account for unit non-response were recently referred to as non-response propensity weighting by Haziza et al. ([24]). These methods view the respondent set as the result of a further phase of sampling, assuming the existence of a response mechanism for which every sampled unit has its own invariably positive response probability. It is also (tacitly) assumed that each unit responds independently to the others. Practically speaking, the respondent set is realized as a sub-sample of the selected sample. A realistic model is adopted to link the unknown response probabilities with some auxiliary variables. The model is subsequently used to estimate the probabilities on the basis of auxiliary information available for all the sampled unit. Unfortunately, in forest inventories responses cannot be viewed as outcomes of dichotomous and independent experiments with unknown probabilities. If some second-phase points cannot be reached, no random experiment can be claimed because they will never be reached. In these situations responses should be viewed as fixed characteristics of the points, in such a way that the population of first-phase points is partitioned into respondent and non-respondent strata. Moreover, the assumption that responses are independent events is likely to be unrealistic in forest surveys. Neighboring points, lying in terrains with the same characteristics, tend to have a similar response pattern, i.e., a sort of spatial contagion is likely to be present among responses. On the basis of these considerations, Fattorini et al. ([18]) conclude that the use of non-response propensity weighting in forest inventory does not seems to be logically defensible.
Alternatively, unit non-response could be handled by a plethora of imputation techniques. Generally speaking, imputation is a procedure in which non response values are replaced by substitutes and estimation is performed on the completed data. As pointed out by Särndal & Lundström ([38]), imputed values are artificial and are customarily obtained by means of a prediction model presuming a relationship between the survey variable and a set of covariates known for all the sampled units. In accordance with the presumed model, commonly used techniques of imputation are, e.g., regression imputation, nearest neighbor imputation, hot deck imputation and multiple imputation (for a review see [27]). Without entering on these techniques, it should be pointed out that no prediction model can be validated in the set of non-respondent units. On the basis of these consideration Fattorini et al. ([18]) conclude that it is difficult to scientifically defend any proposed method/model of imputation.
Because both response and prediction modeling are not sufficiently convincing for non-response treatment in forest inventories, Fattorini et al. ([18]) propose the use of a technique recently referred to as non-response calibration weighting ([24]). Non-response calibration weighting (henceforth NCW) modifies the weights originally attached to each respondent observation. The modified weights are able to estimate without errors the means or totals of a set of auxiliary variables known for all the population units. The rationale behind NCW is obvious: if the calibrated weights guess the means or totals of the auxiliary variables without errors, they should be suitable for estimating the mean or the total of the survey variable, providing a relationship exists between the survey and the auxiliary variables. Noteworthy, the NCW approach does not need to refer explicitly to any model, allowing for a complete design-based treatment in which forest attributes and non-response are both viewed as fixed characteristics.
The theoretical and empirical design-based findings achieved by Fattorini et al. ([18]) look promising. NCW accomplishes the goal of reducing non-response bias when the relationships between interest and auxiliary variables are similar in respondent and non-respondent strata. NCW can even increase the accuracy of estimation with respect to the complete-sample estimation when a close linear relationship exists between the survey and auxiliary variables.
As to the choice of auxiliary information to be used in NCW, it should be mainly guided by cautionary, practical considerations about the nature of the auxiliary variables and their relationships with the survey variable. In presence of non-response, the crucial point is to eliminate non-response bias, because “if an estimator is greatly biased, it is poor consolation that its variance is low” ([38]). Thus, the key requirement is not the strength of the relationships between the survey and auxiliary variables (which affects the sampling variance), but rather the fact that these relationships (linear or not, strong or not) are similar in respondent and non-respondent strata.
Noteworthy, in recent years laser scanning (and, namely, airborne laser scanning, henceforth referred to as ALS) is increasingly being applied to support forest inventories, providing assessment of the height of upper canopy for the surveyed area. A close relationship has been proven between the timber volume (or standing biomass) in inventory plots and the canopy height from ALS surveys ([32], [33], [34], [36], [8], [23], [13]). Obviously, this relationship should hold irrespective of the fact that plots can be reached in the field or not. As such, it is likely to be the same in respondent and non respondent stratum. Therefore, the exploitation of canopy height model (CHM) as auxiliary variable in the NCW approach seems to be a promising strategy to account for non-response in NFIs. It has been recently investigated by Corona et al. ([14]). Because the population of first-phase points is random - being the outcome of the first sampling phase - additional methodological refinements are necessary to apply NCW in forest inventories with respect to the standard methodology proposed by Fattorini et al. ([18]) in which samples are selected from a fixed population.
Quoting from Corona et al. ([14]), denote by R the set of second-phase points reached in the field out of the n points of the second-phase sample S and denote by xi = [1,hi]T the vector where hi denotes the sum of CHM values for all the pixels belonging to the inventory plot centered at the i-th point. If the xis are available for each point i ∈ PF, the mean vectors (eqn. 16):
are known for each k=1, …, K, where PF,k is the set of the NF,k first-phase points lying in the k-th forest type/district, and Hk is the mean of the CHM values within the plots centred at these points. Then Xk can be used in the calibration estimator of Tk, say (eqn. 17):
where pF,k = NF,k / N and (eqn. 18):
and Rk ⊂ R denotes the sub-sample of second-phase points reached in the field among the second-phase points lying in the k-th forest type/district. If the relationship of the forest attribute with CHM height is similar for the respondent and non-respondent points of PF,k, then T(2)CAL,k constitutes an approximately unbiased estimator of Tk. The authors also propose three conservative estimator of the variance of T(2)CAL,k.
The simulation of a two-phase forest inventory performed by Corona et al. ([14]) gave positive insights on the effectiveness of the calibration estimator in reducing the bias induced by non-response, also providing performance comparable with or even better than that achieved by the complete sample estimator. A set of non-response zones were scattered over the forest area, giving rise to a percentage of non-response points of about 9%. The relative downward bias due to non-response was of about 13% , which reduced to 0.2% by the use of calibration estimator with a relative error of 2.2%. Interestingly the calibration estimator showed a performance comparable with that achieved in the case of a complete response. In that case the bias was absent with a relative error of 2.9%. The sole shortcoming of the procedure was the estimation of variance and the subsequent construction of confidence intervals. Indeed, the proposed variance estimators largely overestimated the actual variance, in such a way that the actual gain achieved by the calibration procedure remained undetected by the variance estimates. The construction of less biased variance estimators seems to be one of the necessary steps toward a suitable implementation of this novel idea.
Conclusions
NFIs based on two-phase sampling strategies with first-phase points selected by means of stratified or systematic schemes and second-phase points selected ignoring non-forest points ensure a statistically sound estimation of extents and totals for all variables and domains. From a design-based point of view, the resulting estimators are indeed approximately unbiased and conservative estimators of their variances are available. Moreover, information achieved in the first inventory phase can be used to estimate totals and averages of physical attributes of TOF without any additional field work. Inexpensive auxiliary data from remote sensing and aerial sources can be used at estimation level, i.e., without any modification of the inventory field protocols, as auxiliary information to improve the accuracy of the estimates. Among these information, canopy height from ASL data seems to be the most promising, being able to improve accuracy and, at the same time, to reduce the bias due to missing observations occurred at those points that cannot be reached by forest crews.
Even if canopy height is often available at low or even no cost from ALS surveys carried out on large territories for purposes other than forestry applications, e.g., topographical or hydrogeological surveys ([31]), the availability of ASL data for a whole country (as should be necessary for applications in NFIs) rarely occurs at the moment. However, some countries have already completed national wall-to-wall ASL surveys over their territories, e.g., The Netherlands ([43]), Sweden ([37]), Finland (⇒ http://www.maanmittauslaitos.fi/), Denmark (⇒ http://www.sharpgis.net/), Switzerland (⇒ http://www.swisstopo.admin.ch). If this tendency will be confirmed in the future, ASL data are destined to play a basic role in NFI estimation.
Acknowledgments
The author thanks Gherardo Chirici from the University of Molise, Isernia, Italy, and Piermaria Corona from Consiglio per la Ricerca e Sperimentazione in Agricoltura (CRA), Arezzo, Italy for their support and suggestions on issues regarding forest surveys and Luca Pratelli from Naval Academy, Livorno, Italy, for his continuous support on the theoretical issues.
References
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Department of Economics and Statistics, University of Siena, p.za S. Francesco 8, I-53100 Siena (Italy)
Corresponding author
Paper Info
Citation
Fattorini L (2015). Design-based methodological advances to support national forest inventories: a review of recent proposals. iForest 8: 6-11. - doi: 10.3832/ifor1239-007
Academic Editor
Marco Borghetti
Paper history
Received: Jan 08, 2014
Accepted: Mar 11, 2014
First online: Jun 18, 2014
Publication Date: Feb 02, 2015
Publication Time: 3.30 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 52956
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 43870
Abstract Page Views: 2813
PDF Downloads: 4801
Citation/Reference Downloads: 89
XML Downloads: 1383
Web Metrics
Days since publication: 4226
Overall contacts: 52956
Avg. contacts per week: 87.72
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2015): 24
Average cites per year: 2.18
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Estimation of aboveground forest biomass in Galicia (NW Spain) by the combined use of LiDAR, LANDSAT ETM+ and National Forest Inventory data
vol. 10, pp. 590-596 (online: 15 May 2017)
Research Articles
Integrating area-based and individual tree detection approaches for estimating tree volume in plantation inventory using aerial image and airborne laser scanning data
vol. 10, pp. 296-302 (online: 15 December 2016)
Review Papers
Analysis of full-waveform LiDAR data for forestry applications: a review of investigations and methods
vol. 4, pp. 100-106 (online: 01 June 2011)
Research Articles
Are we ready for a National Forest Information System? State of the art of forest maps and airborne laser scanning data availability in Italy
vol. 14, pp. 144-154 (online: 23 March 2021)
Research Articles
Identification and characterization of gaps and roads in the Amazon rainforest with LiDAR data
vol. 17, pp. 229-235 (online: 03 August 2024)
Research Articles
A LiDAR-based approach for a multi-purpose characterization of Alpine forests: an Italian case study
vol. 6, pp. 156-168 (online: 08 April 2013)
Research Articles
Comparison of wood stack volume determination between manual, photo-optical, iPad-LiDAR and handheld-LiDAR based measurement methods
vol. 16, pp. 243-252 (online: 23 August 2023)
Research Articles
Comparing image-based point clouds and airborne laser scanning data for estimating forest heights
vol. 10, pp. 273-280 (online: 23 February 2017)
Research Articles
High resolution biomass mapping in tropical forests with LiDAR-derived Digital Models: Poás Volcano National Park (Costa Rica)
vol. 10, pp. 259-266 (online: 23 February 2017)
Research Articles
Comparing land use registry and sample based inventory to estimate forest area in Podlaskie, Poland
vol. 10, pp. 315-321 (online: 23 February 2017)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword








