Slope shape effect on runoff and soil erosion under natural rainfall conditions
iForest - Biogeosciences and Forestry, Volume 7, Issue 2, Pages 110-114 (2014)
doi: https://doi.org/10.3832/ifor0845-007
Published: Dec 18, 2013 - Copyright © 2014 SISEF
Research Articles
Abstract
Slope is often non-uniform along the hillslope, with variations describing concave and convex shapes associated with natural hillslopes. This is because runoff generations vary significantly over short distances, with changes in surface alteration during or between flow events on different slope shapes. The aim of this research is to determine the effects of slope shapes on runoff and soil erosion. A field experiment was conducted from September 2007 to September 2009 on hillside field plots located in the northern part of the city of Bartin in northwestern Turkey. The experiment focused on complex topography including uniform, concave, and convex slopes. Nine experimental field plots were established on a 30 per cent slope, including three replications of field plots per different shape treatment. Runoff and soil loss by water erosion were measured in these plots under natural rainfall conditions. A total of 158 rainy days and 69 runoff events were registered over the period of investigation. Runoff and soil loss were greater in uniform plots than in concave and convex plots. The greatest amount of runoff was measured between September 2007 and August 2008 (Period1: P1), with 211.53 mm from uniform plot1 and during September 2008 and August 2009 (Period2: P2) with 430.06 mm from uniform plot3. The lowest runoff quantities with 157.44 and 371.63 mm from concave plot3 and concave plot1, respectively, were measured at P1 and P2. The highest soil loss was recorded at 2.97 kg m-2 and 6.16 kg m-2 during P1 and P2 from uniform plot2 and uniform plot3, respectively, and soil loss was lowest from concave plot3 and concave plot1, with a total of 0.23 kg m-2 and 0.67 kg m-2, respectively. The distribution of eroded soil was separated into >2 mm (coarse) and ≤2 mm (fine) size classes, and suspended quantity in runoff was also determined. Results indicated that the majority of soil lost from the uniform plots is composed of fine particles rather than coarse and suspended material. On the other hand, both concave and convex slopes demonstrated larger variability in the size distribution of eroded particles from individual plots.
Keywords
Introduction
Soil erosion and runoff generation from a field or a basin depend on several parameters, such as climate, soil characteristics, rainfall depth and intensity, and slope morphology. At the hillslope scale, conditions at the surface vary with the topographic positions that can cause different hydrologic regimes and erosion ([12]). Early studies showed that general slope parameters influencing runoff generation and soil erosion are slope gradient, length, and shape ([24]). The effects of length ([14], [15], [20], [5]) and slope gradient ([7], [3], [18]) on soil loss and runoff were studied extensively, with the general conclusions that eroded materials and runoff increase with higher slope steepness ([25], [24], [16], [9], [8]). Moreover, a clear reduction in runoff for each unit of slope length was observed as slope length increased ([10], [2], [19]). However, few research has been conducted on the influence of slope shape on runoff and soil erosion. Gradient is often non-uniform along the hillslope with variations describing concave and convex shapes associated with natural hillslopes. This is because runoff generations vary significantly over short distances, with changes in surface alteration during or between flow events on different slope shapes.
[25], [26]) investigated the effects of slope shapes on soil erosion and runoff. They measured soil loss and runoff from uniform, concave, and convex slopes under simulated rainfall. For slopes of the same average steepness, the results indicated that concave slopes greatly reduced the total sediment loss in comparison to a uniform or convex slope ([26]). Rieke-Zapp & Nearing ([21]) carried out laboratory experiments to determine the relationship between slope shapes and soil erosion using five slope shape treatments. They found that slope shape had a significant impact on rill patterns, sediment yield, and runoff production. The authors expressed that the uniform, nose-shaped, and convex-linear slopes yielded more sediment than the concave-linear and head-shaped slopes.
The aim of this study is to investigate the effect of slope shape on runoff and soil erosion. This study was carried out using the data obtained from September 2007 to September 2009 as a result of two years of field observations using experimental plots on concave, convex, and uniform slope shapes under natural rainfall conditions.
Material and methods
Description of study area
The study was carried out in the Dallica Village experimental area in the northern part of the city of Bartin (northwestern Turkey - 46° 12’ N, 44° 38’ E) at an altitude of 146 m. The area features a humid mesothermal climate with a mean annual precipitation of 1038.2 mm. Most of this precipitation (53%) falls from September to January (data recorded from 1953 to 2008,) and the annual mean temperature is 12.9 °C (data registered from 1963 to 2008). Average temperatures in the province range from 4.1 °C (January) to 21.6 °C (July). The soil of the study area, developed on limestone, is shallow (from 5 to 30 cm deep), fine-textured, stony, calcareous, and classified as clay, composed of 33% sand, 21% silt, and 46% clay. The average bulk density and porosity of the upper 10 cm of soil were 1.36 g cm-3 and 49.38%, respectively. Soil pH was 8.0, electrical conductivity was 0.19 dS m-1, organic carbon content was 31.24 mg gr-1, and total nitrogen content was 2.38 mg gr-1. The soil surface is mainly covered by native herbaceous vegetation and a few small shrub communities. Further details about the vegetation species of the site are given by Kara et al. ([13]).
Methodology
Experimental field design
Experimental plots were established in the summer of 2007, and measurements carried out between September 2007 and September 2009. Nine experimental plots (5.5 m long by 1.87 m wide), consisting of concave, convex, and uniform hillslope at 30% gradient slope, were oriented parallel to the topography. The experimental field was about 100 m in length and located on the upper and middle part of a hill, and the general slope had a southeast orientation. The experimental design included three replications of the field plot (Fig. 1) per different shape (concave, convex, and uniform) treatment. The direction of the plots oriented parallel to the main slope of the field. Each plot was bordered by strips of metal sheet, sunken into the ground at a depth of 20 cm, and buttressed by iron bars on either side of the whole plot to restrict the runoff collection area. A 5-cm diameter flow funnel connected to a gutter was installed in the midway of the lower boundary of each plot. Water and sediment leaving the plot were directed by these funnels into tanks. The storage system consisted of two tanks (Fig. 2), a metal sedimentation box, and a plastic runoff collection tank, arranged in a series on the downslope side of each plot. The sedimentation box and collection tank were covered so that there was no direct precipitation to contribute to the measured water quantities. Runoff and coarse material were primarily mounted in a sedimentation box. A fine- hole field sieve was installed in the sedimentation box in order to keep most coarse material in the box. Water ran down a gutter connected to a hole in the bottom of the sedimentation box to a runoff collection tank with a capacity of 300 l (Fig. 2). Runoff amount and runoff coefficients from each plot were calculated using the volume of water in each tank, which was measured manually within 24 hours of each major rainfall event or after a series of events that were separated by a short time interval. Coarse material and suspended sediment samples were collected as soon as possible after a rainfall event that produced runoff.
Total monthly rainfall amount was measured with a standard rain gauge located at the experimental site. The plots were maintained under bare conditions during the study period. All vegetation was removed from the plots by hoeing.
Natural rainfall events
During the period of experimentation, a total of 158 rainy days were registered. Rainfall amounted to 666.9 mm in 2007, 948.35 mm in 2008, and 774.35 mm in 2009. The largest rainfall event was 167.7 mm on July 15, 2009, but no rain fell during August in both 2008 and 2009 and in February 2008. The average volumes of rainfall in January, February, April, May, June, and August in both years was below monthly average during the study period, but the other months had above average rainfalls according to records from Bartin Meteorology Station, located 3 km east of the study site. Tab. 1 shows monthly rainfall amounts.
Tab. 1 - Monthly rainfall (mm) at Dallica during the experimental period and mean long-term (1953-2008) values for Bartin Meteorology Station. (*): No rainfall events, (**): Long Term.
| Years | Jan | Feb | Mar | Apr | May | June | July | Aug | Sep | Oct | Nov | Dec | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2007 | - | - | - | - | - | - | - | - | 68.3 | 183.5 | 243.6 | 171.6 | 666.9 |
| 2008 | 43.4 | 0* | 133.6 | 27.1 | 35.3 | 37.3 | 175.1 | 0* | 202.7 | 44.2 | 75.9 | 173.9 | 948.4 |
| 2009 | 162.4 | 137.5 | 150.2 | 69.5 | 9.6 | 7.1 | 238.2 | 0* | - | - | - | - | 774.4 |
| LT** | 117.1 | 87.3 | 74.7 | 55.9 | 52 | 67 | 62.7 | 84.4 | 86.5 | 101.4 | 122. | 127.2 | 1038.2 |
Runoff and erosion measurements
The runoff amount per unit area (expressed in mm) was computed as the total runoff amount divided by the plot area. The runoff coefficient represents the percentage of runoff from rainfall which is obtained for each runoff event during the study period. The monthly runoff coefficient was determined as the ratio of monthly runoff depth to monthly rainfall. Coarse sediments were collected from the sedimentation box, and sieved, and then macroaggregates (> 2 mm) and microaggregates (≤ 2 mm) were weighed after they had been air-dried. Samples were collected from different depths in the runoff collection tanks for the calculation of average suspended sediment concentration by weighing after oven-drying the collected samples at 105 °C (g L-1). Sediment concentrations were averaged and multiplied by the total runoff volume to calculate total suspended sediment in runoff the collection tanks. Annual soil losses were calculated as the sum of coarse sediment and suspended sediment volumes.
Data analysis
Statistical analyses were carried out using the SPSS 16.0 statistical package program. The effect of slope shape on runoff and soil loss was determined by one-way analysis of variance (ANOVA). A 95% confidence interval (p<0.05) was chosen to indicate statistically significant differences between samples. Duncan’s multiple range test was used for mean comparisons among samples.
Results
Runoff characteristics
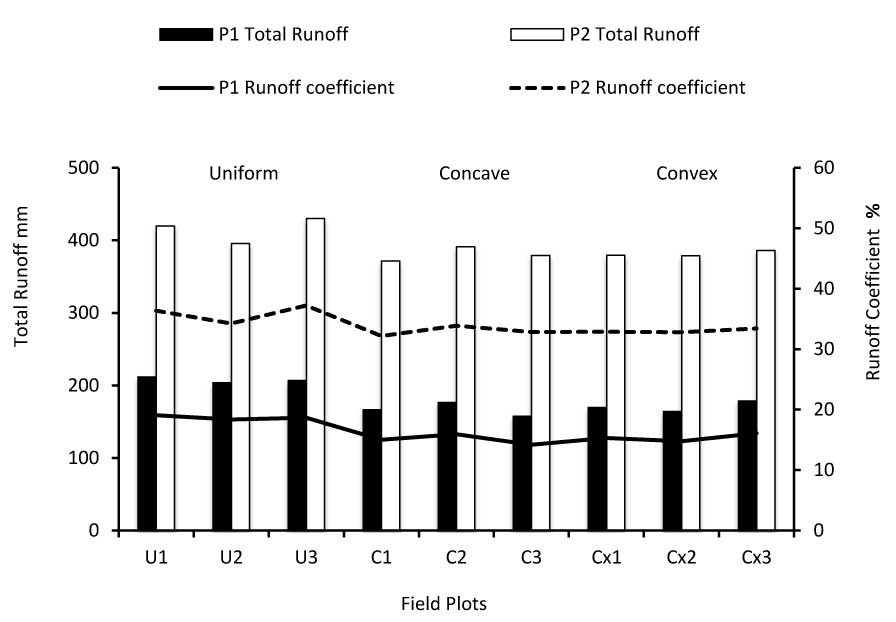
Measurement periods from September 2007 to August 2008 are symbolized by P1, and those from September 2008 to August 2009 are symbolized by P2. A total of 69 runoff events were recorded in 16 months. Total runoff and mean runoff coefficient from the uniform (U), concave (C), and convex (Cx) plots (Fig. 3) were measured. A large amount of runoff was observed during P1 with 211.53, 206.96, and 203.72 mm from uniform plots U1, U3, and U2, respectively. The lowest runoff quantities were observed with 157.44, 163.97, and 166.6 mm from concave plot C3, convex plot Cx2, and C1, respectively. During P2 largest runoff quantities were observed with 430.06, 419.67, and 395.65 mm from U3, U1, and U2, respectively. Lowest runoff quantities were observed with 371.63, 378.83, and 379.27 mm from C1, Cx2, and C3, respectively. The runoff coefficient ranged from 14.18% to 19.05% in P1 and from 31.3% to 37.24% in P2. During July 12-15, 2009, heavy rainfall occurred in the course of four days, in which 233.55 mm of rainfall fell, so the field faced saturation conditions. Thus, during July 2009, a significant proportion of the rainfall to runoff (> 70%) in all plots was observed.
Fig. 3 - Total runoff and mean runoff coefficient on the uniform (U), concave (C), and convex (Cx) plots.
Slope shape and runoff relationships
Monthly runoff amounts were divided into three groups on the basis of mean runoff coefficient as RC1 (< 10%), RC2 (10% < runoff coefficient < 25%), and RC3 (> 25%), except for the extreme value in July 2009. The results showed that there were significant differences (p<0.01 and p<0.05) in the runoff amounts of three slope shapes within RC1 and RC3 groups, respectively. Surprisingly, no statistically significant difference (p>0.05) were detected in runoff amounts within the RC2 group associated with the three different slope shapes (Tab. 2).
Tab. 2 - Statistical summary of runoff based on plots from different slope shape. Values given are the monthly total runoff amounts from each plot. Different letters along the same row indicate significant differences (p<0.05) as from Duncan’s multiple range test.
| Variable | Runoff Coefficient (%) |
N | Uniform | Concave | Convex |
|---|---|---|---|---|---|
| Runoff (mm) |
RC1 | 36 | 3.34 ± 0.30 a | 1.74 ± 0.26 b | 1.81 ± 0.25 b |
| RC2 | 54 | 30.11 ± 2.76 a | 25.85 ± 2.08 a | 26.40 ± 2.09 a | |
| RC3 | 45 | 50.87 ± 2.52 a | 42.72 ± 1.29 b | 43.60 ± 1.08 b |
Soil erosion
The proportion and size distribution of the total soil erosion from the plots are shown in Tab. 3. The total erosion for consecutive periods was substantially higher for uniform plots than for the concave and convex plots. The highest soil erosion was recorded during P1 and P2 from U2 and U3 (2.97 kg m-2 and 6.16 kg m-2); total soil loss from C3 and C1 was lowest, with a total of 0.23 kg m-2 and 0.67 kg m-2, respectively. The particle size distributions of the eroded soil from plots for the two size classes and for the suspended quantity are given in Tab. 3. About two-thirds of the total sediment was ≤ 2 mm in diameter for all plots, with the exception of plot C1. As for concave plots and Cx1 and Cx2, contrary to uniform plots, suspended sediment made up the majority of the eroded soil in P1. In general, the amount of particles > 2 mm eroded from plots was quite low, as were the particles ≤ 2 mm and suspended sediment for consecutive periods.
Tab. 3 - Soil erosion results from slope shape field plots. Values given are the monthly total soil erosion amounts.
| Period | Size distribution of eroded particles (kg m-2) |
Slope shape | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Uniform | Concave | Convex | ||||||||
| U1 | U2 | U3 | C1 | C2 | C3 | Cx1 | Cx2 | Cx3 | ||
| P1 | > 2 mm | 0.23 | 0.53 | 0.19 | 0.01 | 0.05 | 0 | 0.03 | 0.03 | 0.04 |
| 2 mm | 0.98 | 1.89 | 0.8 | 0.02 | 0.02 | 0.01 | 0.08 | 0.12 | 0.14 | |
| Suspended | 0.39 | 0.55 | 0.39 | 0.25 | 0.23 | 0.22 | 0.16 | 0.31 | 0.11 | |
| Total | 1.6 | 2.97 | 1.38 | 0.28 | 0.3 | 0.23 | 0.27 | 0.46 | 0.29 | |
| P2 | > 2 mm | 0.65 | 0.68 | 0.62 | 0 | 0.5 | 0.29 | 0.34 | 0.4 | 0.05 |
| 2 mm | 3.36 | 3.64 | 4.55 | 0.03 | 2.47 | 1.58 | 1.79 | 2.56 | 0.67 | |
| Suspended | 0.94 | 1.35 | 0.99 | 0.64 | 0.61 | 0.5 | 0.24 | 0.75 | 0.17 | |
| Total | 4.95 | 5.67 | 6.16 | 0.67 | 3.58 | 2.37 | 2.37 | 3.71 | 0.89 | |
Slope shape and soil erosion relationships
Analysis of variance was used to test the significance (p<0.05) of the differences in the relationships among soil loss and slope shapes both for P1 and P2 study periods (Tab. 4). Total soil loss for consecutive periods was significantly higher (p<0.05) in uniform plots than in concave and convex plots in P1 and P2.
Tab. 4 - Statistical summary of soil erosion based on plots from different slope shape. Values given are the monthly total soil erosion amounts from each plot Different letters along the same row indicate significant differences (p<0.05) as from Duncan’s multiple range test.
| Variable | Period | N | Uniform | Concave | Convex |
|---|---|---|---|---|---|
| Soil loss kg m-2 | P1 | 72 | 0.24 a | 0.03 b | 0.04 b |
| P2 | 63 | 0.37 a | 0.04 b | 0.11 ba |
Discussion
There are some similarities as well as differences between results in this study and several previous studies. The results of this study indicate that slope shape has a significant effect on runoff (Tab. 2) and soil erosion (Tab. 4). As can be seen in Fig. 3, the uniform slope produced more runoff compared to concave and convex slopes. However, the total amount of soil erosion from the uniform slope was considerably higher than that from a concave or a convex slope (Tab. 3). Similar results have been reported in laboratory experiments by Rieke-Zapp & Nearing ([21]). Meyer & Kramer ([17]) hypothesized that concave profile would erode less and produce less sediment than common uniform, convex, or complex slopes. Hancock et al. ([11]) demonstrated that concave hillslopes can reduce sediment loss by up to five times that of linear slopes. These findings are partly supported by the results of our study. On the contrary, Young & Mutchler ([25]) found that runoff as well as soil loss from a convex slope was much greater than that of concave and uniform slopes. Another study by Young & Mutchler ([26]) suggested that a concave slope produced higher runoff than uniform and convex slopes and, that soil loss from a convex slope was greater than that from concave and uniform slopes. One possible explanation is that our implementation, as in Rieke-Zapp & Nearing ([21]), was carried out in bare soil conditions, and this may be the primary factor together with slope shape effects on soil erosion and runoff. The second factor can also be related to plot length, as in the experiments of Young & Mutchler ([25], [26]), in which plot length was 24 m compared with 5.5 m in this study. It is important to remember that several factors, such as spatial variability on plot scale, and sediment trapped in depressions, and remobilized by raindrop impacts may influence soil erosion and runoff.
Although there are close runoff values between different slopes (Fig. 3), it may not be said for soil erosion on each slope shape (Tab. 3). Total soil erosion in both P1 and P2 from the concave slope was up to 7 and 2.5 times lower and the convex slope up to 6 and 2.5 times lower than the uniform slope, respectively. The variability between uniform and concave slopes may explain the differences in the energy of runoff available for erosion. In concave slopes, runoff velocity was quite low in the middle part of slope; thus, runoff cannot gain enough power to transport soil particles. Similarly, Römkens et al. ([22]) reported that the uniform slope yielded a significantly larger amount of total soil loss than the concave slope. Hancock et al. ([11]) also stated that concave slopes can reduce sediment loss by at least half the amount of the linear slope.
As noted in the results section (Tab. 3), the distribution of particles which are smaller than 2 mm in the eroded sediment taken from all uniform plots is higher than those in P1 and P2. For concave plots except for C1, total sediment yield is dominated by suspended sediment in P1. The proportion of suspended sediment in P2 was less than that in C2 and C3 per ≤ 2 mm size class. The results of this study suggest that the amount of eroded suspended particles was more than in other size classes for two convex plots except in Cx3 in P1. In P2, the ≤ 2 mm size class made up a great portion of the total eroded material for all convex plots. It seems that there are differences among the eroded classes from the convex slope on plot scale. This kind of unexplained variability for plot scale, particularly concave and convex slopes, is not only seen in particle size distribution classes but also in total eroded sediment. The above heterogeneity was unexpected, although Wendt et al. ([23]), Bagarello & Ferro ([4]), and Boix-Fayos et al. ([6]) specified that unexplained variability may be possible in soil erosion among plots. Detachment and transport processes of sediment are different concepts and are controlled by different soil properties, especially in concave and convex slopes. The size and density of detached particles affect the transport limit of sediment ([1]) and slope shape has an effect on the travel distance of individual particles from plots. This does not seem to be the primary factor for concave and convex slopes.
Conclusion
This field experiment indicates that slope shape has a significant effect on soil erosion and runoff. Uniform slope produces more runoff and soil erosion than others, and concave slope produces the least. Soil erosion shows unexplained spatial variability in concave and convex slopes. Fine soil particles (≤ 2 mm) makes up the majority of the eroded soil from uniform slope, and concave and convex slopes demonstrate large variability in the eroded particle size distribution among individual plots and study periods.
References
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Department of Watershed Management, Faculty of Forestry, University of Bartin, TR-74100 Bartin (Turkey)
Department of Watershed Management, Faculty of Forestry, Karadeniz Technical University, TR-61080 Trabzon (Turkey)
Corresponding author
Paper Info
Citation
Sensoy H, Kara Ö (2014). Slope shape effect on runoff and soil erosion under natural rainfall conditions. iForest 7: 110-114. - doi: 10.3832/ifor0845-007
Academic Editor
Giustino Tonon
Paper history
Received: Oct 30, 2012
Accepted: Jul 15, 2013
First online: Dec 18, 2013
Publication Date: Apr 02, 2014
Publication Time: 5.20 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2014
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 71964
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 59265
Abstract Page Views: 3519
PDF Downloads: 7581
Citation/Reference Downloads: 59
XML Downloads: 1540
Web Metrics
Days since publication: 4350
Overall contacts: 71964
Avg. contacts per week: 115.80
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2014): 37
Average cites per year: 2.85
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Short Communications
Seasonal change in soil nitrogen mineralization in young Chamaecyparis obtusa stands at the upper and lower positions on a slope in central Japan
vol. 18, pp. 197-201 (online: 20 July 2025)
Research Articles
Wood-soil interactions in soil bioengineering slope stabilization works
vol. 2, pp. 187-191 (online: 15 October 2009)
Research Articles
Impact of rainfall intensity and cutslope material on sediment concentration from forest roads in northern Iran
vol. 7, pp. 48-52 (online: 21 October 2013)
Research Articles
Spatial heterogeneity of soil respiration in a seasonal rainforest with complex terrain
vol. 6, pp. 65-72 (online: 07 February 2013)
Research Articles
Soil microorganisms at the windthrow plots: the effect of post-disturbance management and the time since disturbance
vol. 10, pp. 515-521 (online: 20 April 2017)
Research Articles
Soil stoichiometry modulates effects of shrub encroachment on soil carbon concentration and stock in a subalpine grassland
vol. 13, pp. 65-72 (online: 07 February 2020)
Research Articles
Soil fauna communities and microbial activities response to litter and soil properties under degraded and restored forests of Hyrcania
vol. 14, pp. 490-498 (online: 11 November 2021)
Research Articles
Soil respiration along an altitudinal gradient in a subalpine secondary forest in China
vol. 8, pp. 526-532 (online: 01 December 2014)
Research Articles
Impact of deforestation on the soil physical and chemical attributes, and humic fraction of organic matter in dry environments in Brazil
vol. 15, pp. 465-475 (online: 18 November 2022)
Research Articles
Comparison of soil CO2 emissions between short-rotation coppice poplar stands and arable lands
vol. 11, pp. 199-205 (online: 01 March 2018)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword