Introduction 

Tree bark differs from wood in terms of its anatomical structure, properties and chemical composition ([20]). Its share in the total weight of the tree stem depends on tree species and most often ranges from 5 to 20 % ([38], [2]). The bark of tree stems and branches is highly differentiated, consisting of meristems, conductive and nonconductive phloem and cortex ([18]). It is a structure that undergoes constant changes due to the dying of some tissues and the growth of others ([11]).

Bark fulfills a number of different functions. It constitutes a natural protective coat of trees and a barrier to pathogens ([7]), while its thickness and density are often important factors, decisive about tree survival in forest fires ([12], [36], [4], [6]). Bark may be used in air pollution biomonitoring ([41]) and it is the environment of numerous organisms, such as mosses, lichens and plasmodial slime molds, whose distribution over the tree stem depends primarily on tree species, bark texture and bark acidity ([5], [42], [24], [35]).

Individual tree species differ from one another in terms of bark thickness and texture. The morphological differentiation of bark also occurs within a single species ([15]). As a result of tree stem thickening, cracks appear in bark and become deeper with tree age, and the direction of cracks determines the appearance of bark ([22]). Although the tree bark surface structure is relatively difficult to parametrize, methods of its measurement have been recently developed. It can currently be measured using the LaserBark^TM device ([44]), which enables automatic and fast measurement of bark microrelief, wavelet analysis ([25]) and the coefficient of development of the interception surface of bark ([15]).

From the point of view of forest hydrology, tree and shrub bark is one of the basic containers which intercept rainwater. Rainfall interception on the plant surface is an important component of the hydrological cycle of the forest environment and depends, among others, on species-related characteristics of plants (leaf size and arrangement, bark roughness), weather conditions, rainfall amount and intensity as well as raindrop size ([13], [26], [28], [17]). The amount of water stored on the plant surface may reach from 6 to 50% of total rainfall ([31], [33], [1], [9]) and the key role in that process is played by the bark layer of trees ([13], [32]).

Bark structure differences between particular tree species affect the water storage capacity of bark and stemflow production ([8], [3], [29]). According to some authors, the maximum water capacity of bark and its wettability are factors affecting the volume and chemistry of the water flowing down the tree stem ([47], [10], [28]). The condition necessary for water flow down the stem is the saturation of its bark with water ([19]). According to Voigt & Zwolinski ([47]) the amount of water flowing down the tree stem depends more on bark properties than on meteorological conditions. It has been observed that trees with rough bark have a higher water storage capacity and generate a smaller stemflow than trees with smooth bark ([46], [26], [27]). Van Stan et al. ([45]) used a LaserBark to compute bark microrelief, ridge-to-furrow amplitude and slope metrics for Fagus sylvatica L. and Quercus robur L. They observed that a smaller ridge-to-furrow amplitude and slope for Fagus sylvatica significantly lowered the bark water storage capacity, which strongly correlated to maximum funneling ratios and permitted stemflow generation at lower rain magnitudes, while larger ridge-to-furrow amplitude and slope values for Quercus robur reduce funneling, diminishing stemflow drainage for larger storms.

Despite a vast literature on plant interception, relatively little is known about the dynamics of rainfall interception by the bark of stems and branches and the factors that regulate this process. As the outer tree layer, bark is exposed to the direct action of atmospheric conditions and it reacts to changes in relative air humidity, often resulting in changes of bark thickness and moisture. For that reason, the object of the present research is the actual hygroscopicity of the bark of selected forest tree species, regarded as a component of the maximum water storage capacity of bark. Actual hygroscopicity S_HA should be understood as the maximum amount of water (expressed in balance units) that can be absorbed from saturated air by bark with particular physical characteristics, assuming that the water is adsorbed only by the outer bark layer, exposed to the direct action of atmospheric conditions. The main research aims include: (1) determination of physical properties (specific density, bulk density and total porosity), actual hygroscopicity and maximum water storage capacity of the stem bark at breast height (1.3 m) of eight forest tree species; (2) demonstration of the relationship between bark actual hygroscopicity and its physical properties; (3) determination of the share of the actual hygroscopicity of bark in its maximum water storage capacity.

  Materials and methods 

The research area

Bark samples were collected in Tokarnia Forest District (49° 46′ 28″ N, 19° 51′ 51″ E), part of Myslenice Forest Division, south Poland. The research area is located in the 8th Carpathian Province, District of the Beskid Makowski and Wyspowy Mts and in the Mezoregion of the Beskid Makowski Mts ([43]). Bark samples were collected from the stems of living trees growing on a mixed mountain forest site, at the altitude from 550 to 800 m a.s.l.

Test material sampling

We focused our study on the bark of 4 coniferous tree species: Pinus sylvestris L., Larix decidua Mill., Abies alba Mill., Picea abies (L.) H. Karst and 4 deciduous tree species: Quercus robur L., Fagus sylvatica L., Acer pseudoplatanus L. and Betula pendula Ehrh. Test samples were collected after the beginning of the vegetation season (May - June 2012) from the stems of living trees at breast height (1.3 m). The test material was collected using a saw, knives and chisels by cutting relatively regular bark pieces with the area ranging from 50 to 200 cm², depending on the thickness of bark and trees. For each species, ten bark samples were collected from trees with the breast-height diameter from 5 to 60 cm.

Laboratory research

In the laboratory, each sample was cut into three. One section was used to analyze the specific density (ρ_s); the second to determine the bulk density (ρ_d), while the third was used in the analysis of the actual hygroscopicity (S_HA) and the maximum water storage capacity (S_v).

Determination of specific density, bulk density and total porosity

Specific density ρ_s of particular bark samples was determined by the standard pycnometer method ([37]) - commonly used to determine the specific density of soil - after grinding the bark in a laboratory grinder and pulverizing it in a porcelain mortar. In order to increase measurement accuracy and prevent the flow of dry particles to the surface of the liquid, the 99.8% ethyl alcohol was used instead of water. Specific density ρ_s (g cm^-3) was calculated according to the following formula (eqn. 1):

where M_s is the dry mass of a pulverized bark sample, determined after its drying at 105 °C (g) and V_s is the volume of the solid phase of a bark sample (cm³).

In the present study, bulk density ρ_d is understood as the ratio of dry mass of the bark to its maximum volume, determined in the state of maximum swelling. According to Raczkowski ([40]), pine bark reaches the state of maximum swelling after about 100 hours of soaking in water. For that reason, before determination of bulk density, bark samples were placed in containers with water for 5 days. Next, their volume was determined with the method of temporary augmentation of the water level in a cylinder, after which the samples underwent 24-hour drying at 105 °C. The bulk density of bark ρ_d (g cm^-3) was determined by the formula (eqn. 2):

where M_s is the dry mass of bark determined after drying a sample at 105 °C (g), and V is the volume of a given bark sample determined in the state of maximum swelling (cm³).

On the basis of specific density ρ_s and bulk density ρ_d, for particular bark samples, total porosity (TP, cm³ cm^-3) was determined using the formula (eqn. 3):

Actual hygroscopicity and maximum water storage capacity

Before the beginning of experiments aimed at determination of actual hygroscopicity S_HA and maximum water storage capacity of bark S_V, individual samples were dried for a few days at 35 °C, until their mass stabilized. After their removal from the dryer, all samples were weighed and their internal and side surfaces were secured with silicone so that during the experiments the water was only adsorbed by their external layer. After the application of silicone, the bark was dried again at 35 °C for 8 hours; then the samples were weighed again in order to determine the mass of the insulating layer of particular bark samples. In the next stage, the insulated samples were placed in desiccators, partly filled with water, in which relative air humidity was 96%. Next, individual bark samples were control-weighed every 2 days until they reached constant mass, which allowed for determination of actual bark hygroscopicity S_HA and the respective relative moisture M. After reaching maximum hygroscopicity, the samples secured with silicone were placed in containers with water for 4 weeks in order to determine their maximum water storage capacity. After that period, the samples were placed vertically in desiccators partly filled with water, where they underwent the process of gravity drainage. On completion of the drainage process, individual samples were weighed and, after removal of the insulating layer, they underwent 24-hour drying at 105 °C.

Actual hygroscopicity S_HA of individual bark samples, expressed in mm of the water column in a bark layer with the thickness of 1 cm, was calculated using the formula (eqn. 4):

where M_H is the mass of a bark sample determined in the state of maximum hygroscopicity (g), M_s is the dry mass of a bark sample determined after its drying at 105 °C (g), V is the volume of a sample (cm³) determined as the ratio of the dry mass of bark M_s to its bulk density ρ_d, and 10 is a factor of conversion into mm of H₂O.

An analogous formula was used to determine maximum water capacity of bark (eqn. 5):

where S_v is the maximum water capacity of bark (mm H₂O in a bark layer with the thickness of 1 cm), M_w is the mass of a bark sample determined in the state of maximum filling with water (g).

Relative moisture of bark M (%), corresponding to its actual hygroscopicity S_HA, was calculated using the formula (eqn. 6):

Data analysis

Statistical data analysis was conducted with the use of the software package STATISTICA^® v.10.0 (StatSoft Inc., Tulsa, OK, USA). Differences in specific densities ρ_s and the actual hygroscopicity of bark S_HA between particular forest tree species was tested by means of one-way ANOVA and the post-hoc Tukey’s test. Departure from normality of data was prior tested by the Shapiro-Wilk test, while the equality of variances by the Levene’s test. In the case of variables showing non-normal distribution (bulk density ρ_d, total porosity TP, relative moisture M, maximum water capacity S_v and the share of actual hygroscopicity in the maximum water storage capacity of bark), differences were tested using the non-parametric Kruskal-Wallis test and the Dunn post-hoc test. All differences were tested at the significance level α = 0.05.

Analysis of the relation of the share of actual hygroscopicity S_HA in water storage capacity S_v to the physical and retention properties of bark was conducted by means of linearized non-linear regression. Independent variables were selected on the basis of the corrected coefficient of determination (R²_adj), the standard estimation error, distribution of residual values and the distribution of residual values in relation to values predicted by the equation of regression. The redundancy of variables was evaluated on the basis of the variance inflation factor (VIF) calculated as follows (eqn. 7):

where R_j² is the coefficient of determination of a given variable X_j for the other explanatory variables in the model.

  Results 

Physical properties of bark

Specific density and bulk density

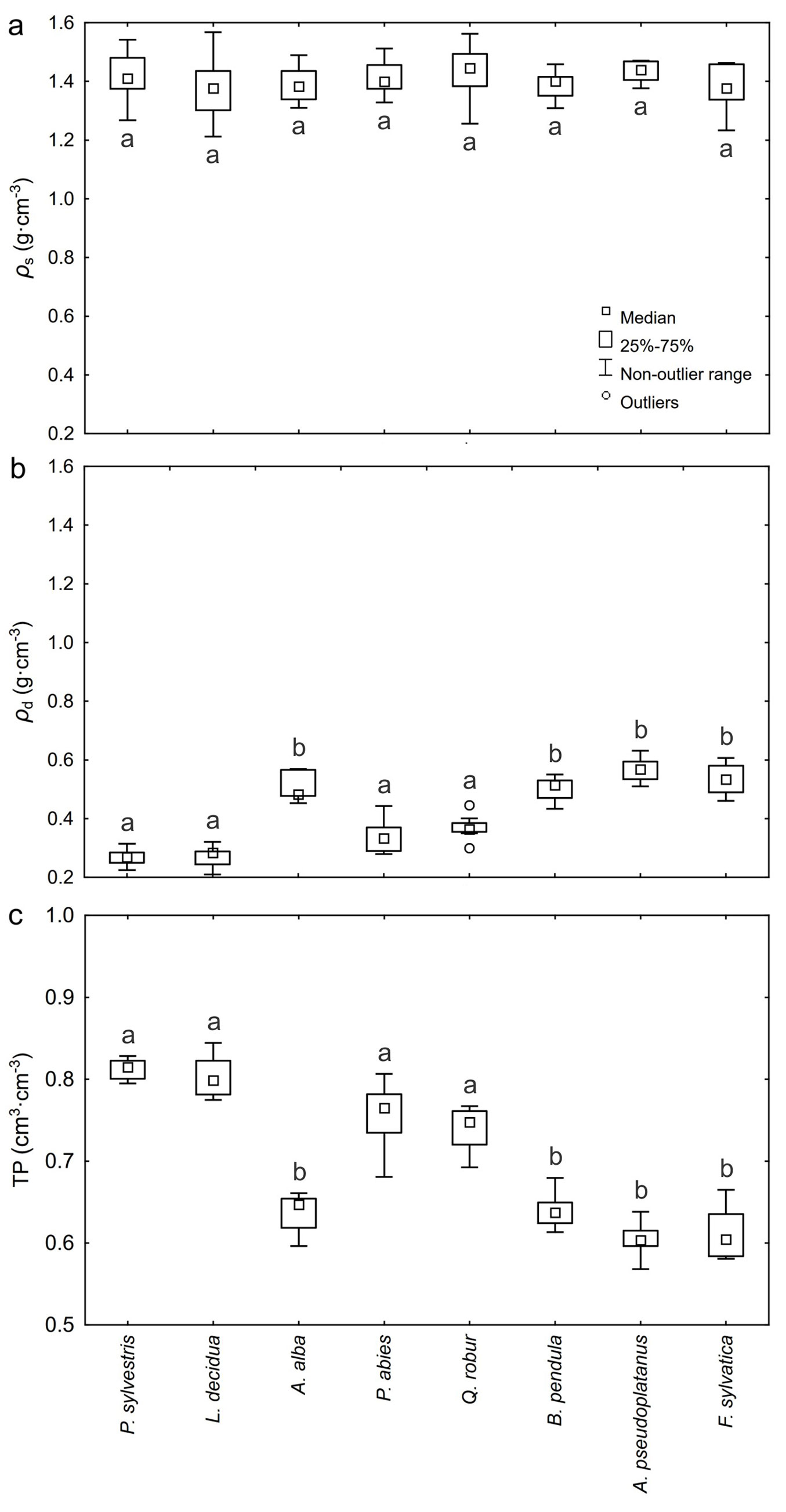
The distribution of specific density ρ_s and bulk density ρ_d, determined for the bark of individual forest tree species is presented in Fig. 1a and Fig. 1b. Specific density of bark ρ_s ranges from 1.212 g cm^-3 (L. decidua, DBH = 15 cm) to 1.562 g cm^-3 (Q. robur, DBH = 29 cm). No significant differences were found between particular tree species in terms of specific density of bark ρ_s (Fig. 1a); the lowest mean specific density ρ_s was obtained for the L. decidua bark (1.373 ± 0.033 g cm^-3), while the highest was observed for the A. pseudoplatanus bark (1.434 ± 0.011 g cm^-3).

Fig. 1 - Range of variation of (a) specific density ρ_s, (b) bulk density ρ_d and (c) total porosity TP of the bark of the forest tree species analyzed. Different letters indicate significant differences between species after Tukey’s or Dunn’s post-hoc tests (p < 0.05).

  Enlarge/Shrink   Download   Full Width  Open in Viewer

Bulk density of bark ρ_d showed values from 0.210 g cm^-3 (L. decidua, DBH = 35 cm) to 0.631 g cm^-3 (A. pseudoplatanus, DBH = 34 cm). For the bark of all coniferous species considered jointly, the mean value of bulk density ρ_d amounted to 0.346 g cm^-3, while for deciduous species it was 0.494 g cm^-3. The highest variation of bulk density characterized the bark of P. abies (17.05%), while the lowest was found for the bark of A. pseudoplatanus (6.99%). The highest mean value of bulk density ρ_d was obtained for the bark of A. pseudoplatanus (0.567 ± 0.040 g cm^-3), while the lowest for the bark of P. sylvestris (0.267 ± 0.008 g cm^-3) and L. decidua (0.269 ± 0.011 g cm^-3).

Total porosity

The range of total porosity TP of the bark of all forest tree species is presented in Fig. 1c. Porosity showed values ranging from 0.57 cm³ cm^-3 (A. pseudoplatanus, DBH = 34 cm) to 0.84 cm³ cm^-3 (L. decidua, DBH = 21 and 35 cm). For the bark of all coniferous species considered jointly, the mean value of total porosity TP was 0.75 ± 0.01 cm³ cm^-3, while for deciduous species it was 0.65 ± 0.01 cm³ cm^-3. The highest mean values of TP were obtained for P. sylvestris bark (0.81 ± 0.01 cm³ cm^-3) and L. decidua (0.80 ± 0.01 cm³ cm^-3), while the lowest for A. pseudoplatanus (0.60 ± 0.01 cm³ cm^-3) and F. sylvatica bark (0.61 ± 0.01 cm³ cm^-3). For the bark of A. alba, P. abies, Q. robur and B. pendula, the mean values of total porosity TP were, respectively, 0.64 ± 0.01, 0.75 ± 0.01, 0.74 ± 0.01 and 0.64 ± 0.01 cm³ cm^-3.

Actual hygroscopicity of bark

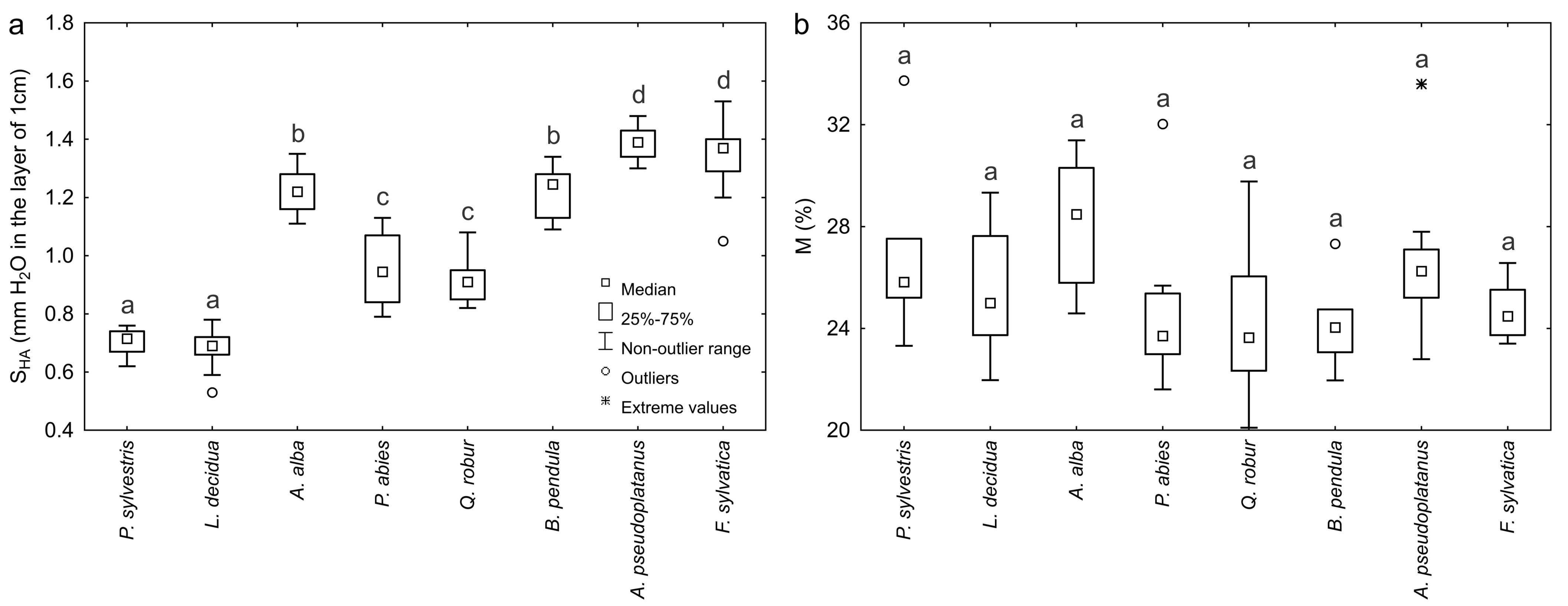
The range of variation of actual hygroscopicity S_HA and the corresponding moisture M of the bark of individual forest tree species is illustrated in Fig. 2a and Fig. 2b. Actual hygroscopicity S_HA ranged from 0.53 mm (L. decidua, DBH = 35 cm) to 1.53 mm of water (F. sylvatica, DBH = 23 cm) in the bark layer with the thickness of 1 cm. The mean value of actual hygroscopicity S_HA of the bark of all coniferous species considered jointly amounted to 0.89 ± 0.04 mm, while for deciduous species it was 1.21 ± 0.04 mm. The highest variation of S_HA characterized the P. abies bark (12.53%) while the lowest was observed for the bark of A. pseudoplatanus (4.09%). The highest mean values of actual hygroscopicity S_HA were obtained for A. pseudoplatanus bark (1.39 ± 0.02 mm) and F. sylvatica bark (1.33 ± 0.04 mm), while the lowest were found for L. decidua (0.68 ± 0.02 mm) and P. sylvestris bark (0.71 ± 0.01 mm). Mean hygroscopicity S_HA of the bark of A. alba, P. abies, Q. robur and B. pendula was, respectively: 1.22 ± 0.03, 0.95 ± 0.04, 0.92 ± 0.02 and 1.22 ± 0.03 mm. Significant differences in the bark S_HA were found between the majority of forest tree species (Fig. 2a).

Fig. 2 - The range of variation of (a) actual hygroscopicity S_HA and (b) relative moisture M (corresponding to actual hygroscopicity) of the bark of different forest tree species. Different letters indicate significant differences between species after Tukey’s or Dunn’s post-hoc tests (p < 0.05).

  Enlarge/Shrink   Download   Full Width  Open in Viewer

Relative bark moisture M, corresponding to its actual hygroscopicity S_HA, ranged from 20.1% (Q. robur, DBH = 29 cm) to 33.7% (P. sylvestris, DBH = 5 cm). The mean value of M of all coniferous species considered jointly was 26.4 ± 0.5 %, while in the case of deciduous species it was 25.1 ± 0.4 %. The highest variation of M was observed for the bark of Q. robur (12.48%), P. abies (12.37%) and P. sylvestris (12.33%), while the lowest for the bark of F. sylvatica (4.67 %). The mean values of the bark M were similar in the case of P. sylvestris, L. decidua, A. alba, P. abies, Q. robur, B. pendula, A. pseudoplatanus and F. sylvatica (26.8 ± 1.2, 25.7 ± 0.9, 28.2 ± 0.7, 24.6 ± 1.0, 24.2 ± 1.1, 24.2 ± 0.8, 26.6 ± 0.9 and 24.7 ± 0.4 %, respectively). On the basis of the Kruskal-Wallis test, no statistically significant differences were noted in relative bark moisture M between particular forest tree species (Fig. 2b).

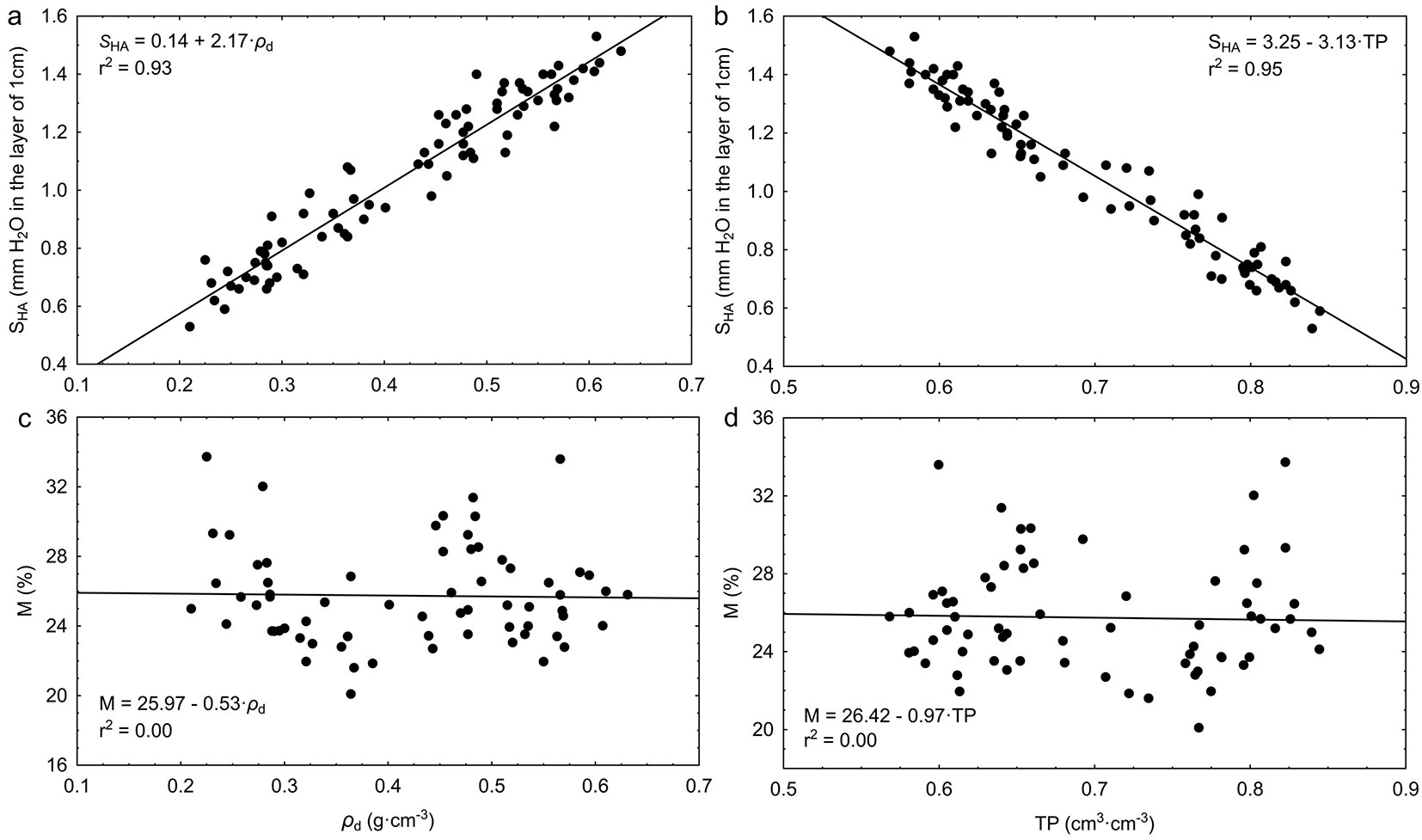
Actual hygroscopicity S_HA showed a strong dependency on bulk density: along with an increase of density, the hygroscopic abilities of bark also grow (Fig. 3a). An opposite dependency was noted in relation to total porosity TP (Fig. 3b). Contrastingly, bark hygroscopicity, expressed in relative units, did not show any relation to the physical properties of bark (Fig. 3c and Fig. 3d).

Fig. 3 - Relationships between: (a) actual hygroscopicity S_HA and bulk density ρ_d; (b) actual hygroscopicity S_HA and total porosity TP; (c) relative moisture M (corresponding to actual hygroscopicity S_HA) and bulk density ρ_d; (d) relative moisture M and total porosity TP of bark of the analyzed forest tree species.

  Enlarge/Shrink   Download   Full Width  Open in Viewer

The share of actual hygroscopicity in maximum water storage capacity of bark

The range of variation of maximum water capacity S_v of the bark of particular forest tree species is presented in Fig. 4a. S_v rangeg from 3.60 mm (B. pendula, DBH = 9 cm) to 7.39 mm (P. abies, DBH = 25 cm) of water in a bark layer with the thickness of 1 cm. The mean value of the bark S_v of all coniferous species considered jointly amounted to 5.83 mm, while for deciduous species it was 5.76 mm. The highest variation of water storage capacity characterized the bark of P. sylvestris (18.1%) and L. decidua (17.6%), while the lowest was found for F. sylvatica bark (6.0%). The highest mean value of S_v was obtained for the bark of P. abies (6.58 ± 0.17 mm), while the lowest for the bark of B. pendula (4.77 ± 0.19). For the bark of P. sylvestris, L. decidua, A. alba, Q. robur, A. pseudoplatanus and F. sylvatica, the mean value of water storage capacity S_v was, respectively: 5.39 ± 0.31, 5.35 ± 0.30, 5.99 ± 0.15, 5.85 ± 0.15, 6.28 ± 0.18 and 6.15 ± 0.12 mm.

Fig. 4 - The range of variation of (a) maximum water capacity S_v and (b) the share of actual hygroscopicity S_HA in maximum water capacity S_v of the bark of particular forest tree species. Different letters indicate significant differences between species after Tukey’s or Dunn’s post-hoc tests (p < 0.05).

  Enlarge/Shrink   Download   Full Width  Open in Viewer

The range of variation of the share of actual hygroscopicity S_HA in maximum water storage capacity of bark S_v of particular forest tree species is illustrated in Fig. 4b. Actual hygroscopicity S_HA constitutes from 9.6 % (L. decidua, DBH = 35 cm) to 30.3 % (B. pendula, DBH = 9cm) of the maximum water storage capacity of bark S_v. The average share of S_HA in S_v of the bark of all coniferous species considered jointly was 15.4 ± 0.60 %, while for deciduous species it was 21.4 ± 0.70 %. The largest variation in the share of actual hygroscopicity S_HA in S_v characterized the bark of L. decidua (22.8%) and P. sylvestris (17.1%) while the lowest was observed for the bark of A. alba (8.1%) and A. pseudoplatanus (8.9%). The bark of B. pendula had the highest mean share of hygroscopicity S_HA in water storage capacity S_v (25.9 ± 1.10 %), while L. decidua (13.1 ± 0.94 %) and P. sylvestris (13.4 ± 0.72 %) had the lowest mean share. For the bark of A. alba, P. abies, Q. robur, A. pseudoplatanus and F. sylvatica, the mean S_HA was, respectively: 20.4 ± 0.53, 14.6 ± 0.76, 15.7 ± 0.49, 22.3 ± 0.63 and 21.7 ± 0.76 %.

The percentage of actual hygroscopicity of bark S_HA in water storage capacity S_v showed a dependency from the total porosity of bark and its maximum water storage capacity. This dependence is described by the following formula, which accounted for nearly 95 % of the total variation (eqn. 8):

where S_HA(%S_v) is the share of actual hygroscopicity of bark in its maximum water capacity (%), TP is the total porosity of bark (cm³ cm^-3) and S_v is the maximum water storage capacity of bark (mm H₂O in a bark layer with the thickness of 1 cm). Significance of the parameters of eqn. 8 is presented in Tab. 1.

  Discussion 

The lack of significant differences in specific density of bark between particular tree species implies that the variation in total porosity of the bark is mainly related to its bulk density. This may be proved by the results displayed in Fig. 1. On their basis it may be stated that differences in bulk density between particular tree species fairly corresponds to differences in their total porosity. Interspecies variation in bulk density of the bark was also reported by Bauer et al. ([6]). According to Meyer et al. ([34]), the density of inner bark may be lower than the density of outer bark, thus differences in the bulk density of bark between species may be related to different proportions of rhytidome to inner bark. According to Quilhó & Pereira ([39]), bulk density of bark along the stems of individual trees is less varied. These authors demonstrated that possible differences in the density of bark of Eucalyptus globules Labill. may be related to environmental conditions, affecting the structure and chemical properties of the bark ([48]).

The differences in the actual hygroscopicity of bark observed between species may be related not only to differences in their physical properties, but also to the chemical composition of cell walls, which is a species-related feature of bark. For example, the bark cellulose content in birch is 4 times smaller than in pine and spruce, while the suberin content is over 10 times higher. Further, pine bark contains nearly 16% more lignin than spruce bark ([11]).

Interspecies variation of bark hygroscopicity had been indicated by Young ([49]). He showed that among 20 tested tree species the highest hygroscopicity expressed in relative units characterized the bark of Pinus sylvestris L. (40.1%), while the bark of Carya opata (Mill.) K. Koch had the lowest (13.6%). According to Kapur & Narayanamurti ([16]), the bark hygroscopicity of different species ranges from 22 to 28 %. As shown in Fig. 3, hygroscopicity expressed in relative units is neither related to the store of water in bark in its balance expression nor to its physical properties. The bark with higher density and lower porosity, while having the same moisture, usually contains more water than the bark with lower density. A similar pattern may be observed for forest soils. According to Kucza ([23]), soil moisture changes expressed in relative units allow for determining the direction of changes, but no quantitative assessment of water balance is possible. In other words, soil water storage cannot be directly inferred from the relative ground moisture, as two soil sediments having the same relative moisture but differing in their granulometric composition and porosity may show different water storage capability. Based on the above reason, it may be concluded that relative moisture is a poor measure of water retention capabilities of the bark.

As shown in Fig. 4b, the actual hygroscopicity of bark may constitute a considerable share of its maximum water storage capacity, reaching even 30% in the case of birch. This implies that during rainfall bark retention may be reduced by as much as 10-30%, depending on tree species. This also means that hygroscopicity of bark may constitute a significant component of the water balance of forest ecosystems. Therefore, the knowledge of actual hygroscopicity of the bark is an important stand parameter and the proposed method may be used for quantifying the degree of bark retention before rainfall occurrence.

It should be emphasized that our results are preliminary as the study was conducted only on bark samples collected at tree breast height. Hutchinson & Roberts ([14]) showed that stemflow is generated mainly in the top tree crowns, likely due to a lower water storage capacity of the bark which is usually thinner ([30]). Vertical variation of the bark water storage capacity has been reported by Levia & Wubbena ([30]) and calls for the analysis of the vertical variation of bark hygroscopicity. However, considering the strong dependence of bark hygroscopicity on its physical properties (Fig. 3) as well as the low variation of bark bulk density along the stems of individual trees ([39]), it may be assumed that the vertical variation of bark hygroscopicity could be very small, while its share in total water storage capacity should increase with the height along the stem.

The main differences found in bark hygroscopicity among species concern its maximum values (Fig. 2a). Wood hygroscopicity exhibits a peculiar dynamics, dependent on air temperature and humidity, among others ([21], [22]). Considering the inter-specific variation in bark morphology and its variability which increases with tree age ([15]), it may be assumed that the dynamics of bark hygroscopicity also depends on tree species and age. Furthermore, bark hygroscopicity dynamics is expected to modify the microclimate in the forest. Indeed, latent heat is released to the atmosphere during steam condensation in contact with bark or it is absorbed from the atmosphere during water evaporation from bark. For that reason, water absorption/evaporation by/from the bark may be an important factor affecting air temperature and humidity within a stand. However, the physical evaluation of that process requires further research focused on the dependence of the dynamics of bark hygroscopicity on changes in air humidity and temperature, on species and age of the stand as well as on the total surface of the bark of tree stems and branches.

  Conclusions 

In this study, the variation of several physical properties of the bark were analyzed in Pinus sylvestris, Larix decidua, Abies alba, Picea abies, Quercus robur, Fagus sylvatica, Acer pseudoplatanus and Betula pendula. It was found that the bark of all coniferous species is generally characterized by a lower bulk density and a higher total porosity compared to deciduous species.

Actual hygroscopicity of bark (expressed in balance units) increased with increasing bulk density and decreasing total porosity of the bark. We found that relative moisture is a poor measure of bark water retention capability. Significant differences in actual hygroscopicity of the bark were found between most of the forest tree species considered, while no differences were observed in terms of relative bark moisture. Depending on tree species, actual hygroscopicity may reach 10-30% of the maximum water storage capacity of the bark.

  Acknowledgments 

This research was financed by the Ministry of Science and Higher Education of the Republic of Poland (grant number: BM/4419/KIL/12). The authors thank two anonymous reviewers for their many valuable and helpful suggestions.

  References