Modelling dasometric attributes of mixed and uneven-aged forests using Landsat-8 OLI spectral data in the Sierra Madre Occidental, Mexico
iForest - Biogeosciences and Forestry, Volume 10, Issue 1, Pages 288-295 (2017)
doi: https://doi.org/10.3832/ifor1891-009
Published: Feb 11, 2017 - Copyright © 2017 SISEF
Research Articles
Abstract
Remote sensors can be used as a robust and effective means of monitoring isolated or inaccessible forest sites. In the present study, the multivariate adaptive regression splines (MARS) technique was successfully applied to remotely sensed data collected by the Landsat-8 satellite to estimate mean diameter at breast height (R2 = 0.73), mean crown cover (R2 = 0.55), mean volume (R2 = 0.57) and total volume per plot (R2 = 0.41) in the forest monitoring sites. However, the spectral data yielded poor estimates of tree number per plot (R2 = 0.22), the mean height (R2 = 0.25) and the mean diameter at base (R2 = 0.38). Seven spectral bands (band 1 to band 7), six vegetation indexes and other derived parameters (NDVI, SAVI, LAI, FPAR. ALB and ASR) and eight terrain variables derived from the digital elevation model (elevation, slope, aspect, plan curvature, profile curvature, transformed aspect, terrain shape index and wetness index) were used as predictors in the fitted models. To prevent over-parameterization only some of the predictor variables considered were included in each model. The results indicate the MARS technique is potentially suitable for estimating dasometric variables from using spectral data obtained by the Landsat-8 OLI sensor.
Keywords
Multivariate Adaptive Regression Splines, Mixed Forest, Uneven-aged Forest, Stand Variables, Remote Sensing, Terrain Features
Introduction
The Sierra Madre Occidental (SMO) mountain range is of great ecological interest due to its environmental heterogeneity, which is attributed to the broad physiographical and climatic diversity in the area. Moreover, the SMO shelters uneven-aged and species-rich pine oak forests that are economically important ecosystems for Mexico and other parts of the world. The SMO crosses several states in western Mexico, including the state of Durango (the SMO occupies 71.5% of the surface area of the state). The state covers a total area of 12.3 million ha, of which 9.1 million ha (74.35% of the land in the state) is forestland managed by 11 Regional Forest Management Units (UMAFORES). A large part of the forestland (4.9 million ha) is occupied by temperate forest and is subjected to precipitation levels of between 800 and 1200 mm per year, with frost occurring in winter as a result of the combination of low temperatures and humid winds from the Pacific Ocean; a smaller area of this land (0.5 million), affected by warmer climate, is occupied by forest classified as rainforest ([42]). The state of Durango generates between 25% and 30% of the national timber production, producing a total of 1.5 million m3 of roundwood per year, and promotes forest reserves as important sources of environmental services ([30]).
Estimation of diverse dasometric variables in forest stands is a fundamental aspect of forest inventories. Commercial volume is particularly important in forest management and is valuable for the conservation of diverse forest ecosystems and for improving the economic productivity of forests ([19]). Other stand variables are also important in forest management, such as diameter at breast height, total height, crown cover, basal area and plant biomass. Stand variables are usually measured on the ground by forest inventory teams in field surveys covering large areas ([43]); however, such surveys are both expensive and time-consuming ([21]).
Use of remote sensors is a cost-effective method of collecting data in large inaccessible areas and provides an alternative source of data for extrapolating and estimating forest variables ([16], [37]). The data obtained can be rapidly updated and compared with existing data, and the method can be easily integrated with Geographical Information Systems. These methods have been successfully combined in several studies, and statistically significant correlations between the remotely-sensed data (captured by Landsat satellite sensors) and field-measured data have been reported for diameter at breast height, age and total height ([11]), volume ([23], [37]) and biomass ([31], [27], [50]). The aim of the present study was to analyze the relationship between a set of field-measured dasometric variables and spectral data obtained by the Landsat-8 OLI (Operational Land Imager) sensor and data derived from a digital elevation model, aimed at estimating the total number of trees per plot, crown cover, mean diameter at base (0.30 m), mean diameter at breast height (1.30 m), mean height, mean volume and total volume per plot in a mixed uneven-aged forests in the Sierra Madre Occidental.
Material and methods
Study area
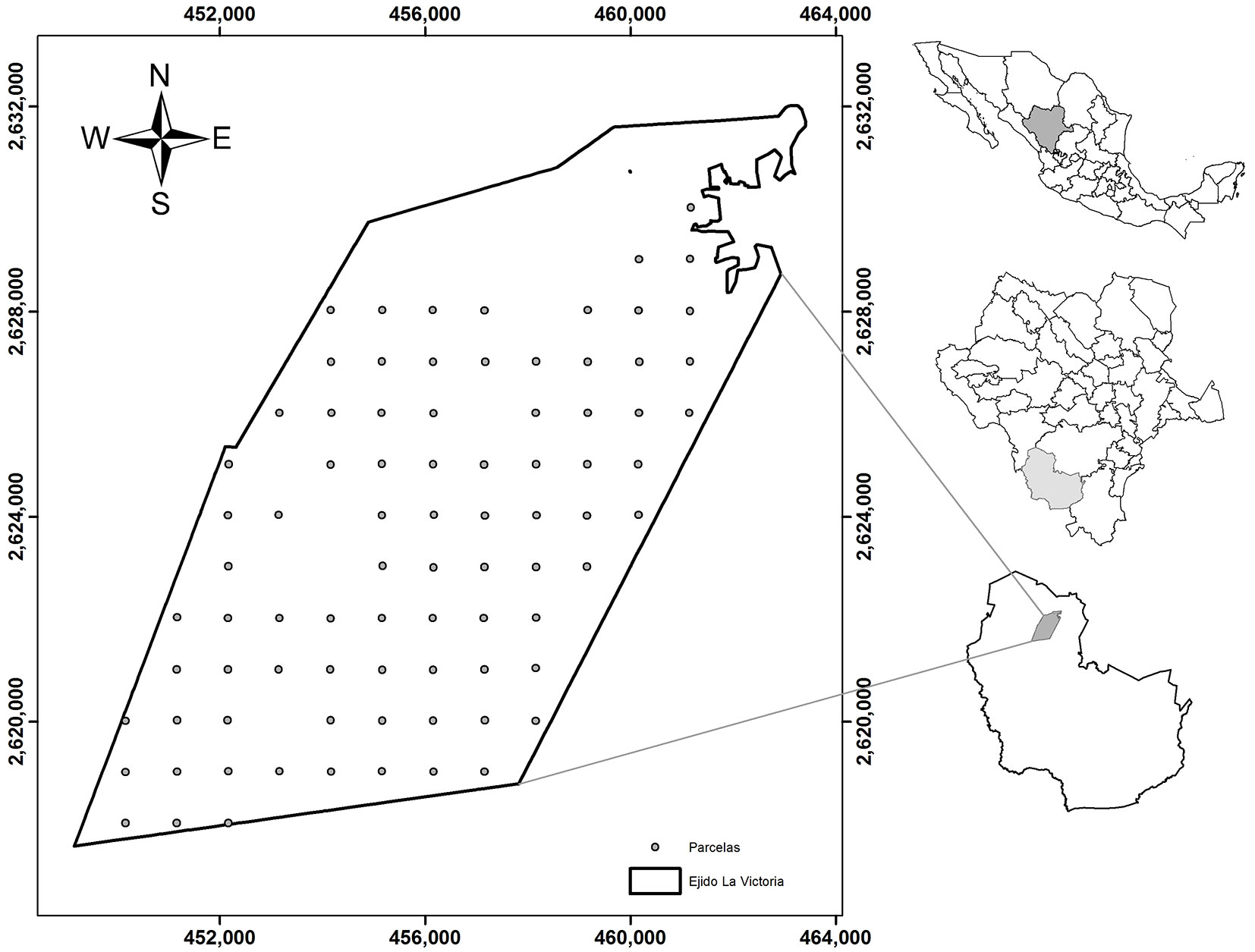
The study was carried out in the Ejido La Victoria (surface area: 10.810 ha), located in the Sierra Madre Occidental in the municipality of Pueblo Nuevo, state of Durango, Mexico (Fig. 1). Site elevation ranges between 2245 and 2870 m above sea level, according to the data obtained from the digital elevation model (DEM) developed by the National Institute of Geography and Statistics of Mexico ([26]). The forests in the study area show a rich biodiversity and include at least 12 coniferous tree species (of which 10 are Pinus species) and 5 species of Quercus. The dominant types of vegetation in the area are mixed conifer forest and pine-oak forest ([46], [22]). The main species present are: Pinus cooperi, P. durangensis, P. engelmannii, P. leiophylla, P. strobiformis, P. teocote, P. herrerae, Juniperus deppeana, Quercus sideroxil and Q. crassifolia ([33]).
Fig. 1 - Maps showing the location of the study area and sample plots used in the study: (right, top to bottom) the State of Durango in Mexico; the municipality of Pueblo Nuevo in the State of Durango; the Ejido La Victoria in the municipality of Pueblo Nuevo. The area covered by the Ejido La Victoria is outlined in the large inset.
Field sampling
A systematic sampling method (1 × 1 km between plots) was used to locate the sampling plots in the study area. In total, 83 circular sampling plots each of surface area 1000 m2 were established. The plots were georeferenced relative to a reference system (WGS 84 Datum / UTM zone 13N). The plot data were obtained with the aid of a submeter GNSS receiver, tree calipers (Haglof, Sweden), hypsometer (Vertex IV®, Haglof, Sweden) and metric tape. The following variables were measured in each plot, taking into account all the trees with diameter at breast height (DBH) larger than 5 cm: tree number (N), diameter at base (DB in cm, measured at 0.30 m above the ground), DBH (in cm, measured at 1.30 m above the ground), total height (HT in m) and crown diameter (CD in m). The volume (V in m3) per plot was estimated using specific allometric equations developed by Corral-Rivas et al. ([8]) for the same study area; the descriptive statistics corresponding to the response variables are shown in Tab. 1.
Tab. 1 - Descriptive statistics for the response variables in each of 83 plots (of surface area, 1000 m2). (STD): standard deviation.
| Stand variable | Mean | STD | Min | Max |
|---|---|---|---|---|
| Tree number per plot (N) | 79.53 | 58.02 | 7.00 | 430.00 |
| Mean diameter at base 0.30 m (cm - DB mean) | 21.40 | 6.41 | 10.79 | 41.24 |
| Mean diameter at breast height 1.30 m (cm - DBH mean) | 17.96 | 5.79 | 8.05 | 35.45 |
| Mean height (m - H mean) | 10.95 | 3.17 | 6.01 | 23.80 |
| Mean crown diameter (m - CD mean) | 3.85 | 0.91 | 1.88 | 6.54 |
| Mean volume (m3 - V mean) | 0.42 | 0.30 | 0.06 | 1.68 |
| Total volume (m3) per plot (TV) | 24.98 | 11.78 | 1.31 | 67.14 |
Datasets
Source of spectral data
The image used in the study was captured by the Landsat-8 OLI sensor (LC80310442014018LGN00) and supplied by the USGS Global Visualization Viewer Server (⇒ http://glovis.usgs.gov/). The image was captured at about the same time as the field sampling was carried out (January, 2014). The images were obtained as a L1T level product (i.e., they were geometrically corrected with ground control points and the DEM). The satellite image was digitally preprocessed by radiometric correction and atmospheric and topographic techniques, following the procedures established in the ATCOR3® module (Atcor for Erdas Imagine - [13]) developed for mountainous areas and implemented with ERDAS® IMAGINE® 2013 software ([13]). The digital levels (DL) of each of the bands (Tab. 2) were converted to surface reflectance values by reading the model parameters and the orbit of the geometrical satellites included in the image metadata. Bands 1 to 7 (B1, B2, B3, B4, B5, B6 and B7) of Landsat-8 OLI were used in the present study.
Tab. 2 - Spectral bands, wavelength, spatial resolution and abbreviated name of the Landsat-8 OLI sensor.
| Band number | Wavelength (µm) |
Spatial r esolution |
Abbreviation |
|---|---|---|---|
| Band 1 - Coastal aerosol | 0.433-0.453 | 30 m | B1 |
| Band 2 - Blue | 0.450-0.515 | 30 m | B2 |
| Band 3 - Green | 0.525-0.600 | 30 m | B3 |
| Band 4 - Red | 0.630-0.680 | 30 m | B4 |
| Band 5 - Near Infrared (NIR) | 0.845-0.885 | 30 m | B5 |
| Band 6 - Short-Wave Infrared (SWIR) 1 | 1.560-1.660 | 30 m | B6 |
| Band 7 - Short-Wave Infrared (SWIR) 2 | 2.100-2.300 | 30 m | B7 |
A number of vegetation indexes and other derived parameters (normalized difference vegetation index, NDVI; soil adjusted vegetation index, SAVI; leaf area index, LAI; fraction of photosynthetically active radiation, FPAR; albedo, ALB; absorbed shortwave solar radiation, ASR) were computed from the atmospherically and topographically corrected image bands and then included in the stand variables estimation models for evaluation as possible regressor variables (Tab. S1 in Supplementary material).
Terrain variables
These variables have influence on forest species composition, tree height growth, and other forest stand variables ([32], [40]). First order variables included: elevation (DEM), slope (SLOPE), transformed aspect (TRASP), profile curvature (PROFCURV), plan curvature (PLANCURV) and curvature (CURV); and second order variables were: terrain shape index (TERRSHPIN2) and wetness index (WETIND). Terrain parameters were generated in the software ArcGIS 10® ([14]), with a 5×5 low pass filtered DEM ([26]) and included as candidate variables in the models (Tab. S2 in Supplementary material). These parameters are potentially related to key features affecting forest stand development, such as overall climate characteristics, insolation, evapotranspiration, run-off, infiltration, wind exposure and site productivity. Some of these terrain features are widely used in hydrological, geomorphological and ecological studies ([47]), whereas others are used more specifically for vegetation and forest assessment ([32], [40]).
Dataset integration
The sample plots were geopositioned with the aim of extracting the pixel value average with an associated buffer of 18-meter radius for geolocalization of the plots. The values were extracted using the raster package available in the R statistical software ([39]). Finally, a database was constructed with the mean stand variables values for each plot: the corrected bands of the Landsat-8 OLI sensor (7 bands), the vegetation indexes (6 indexes) and the terrain variables derived from the DEM (8 variables).
Statistical analysis
As the Shapiro-Wilks test revealed that the data were not normally distributed, the multivariate adaptive regression splines (MARS) technique was used for model construction. The MARS technique is an innovative, flexible method that constructs models for continuous, categorical or binary-type dependent and/or independent variables. It is a non-parametric regression technique based on constructing flexible models by fitting data to linear regressions in segments, combination of which generates local models where the relationship between the predictive and response variables may be linear or non-linear and which also incorporate interactions between variables. Each segment of the regression line represents a stretch of linear response to the variable and is denominated the basic function; the final model consists of the entire set of basic functions. The model can be represented so that it separately identifies additive contributions and those associated with different multivariate interactions ([18]). The general form of the MARS non parametric regression model, formulated on the dependent y variable and the x predictors, is as follows (eqn. 1):
where ε is the error, and f (x) is the unknown regression function, derived as follows (eqn. 2):
where β0 is the intercept of the model, Bm (x) is the mth basis function, βm is the coefficient of the mth basis function, and M is the number of basis functions in the model. Each basis function Bm(x) takes one of the following two forms: (i) a hinge function of the form max(0, x-k) or max(0, k-x), where k is a constant value; (ii) a product of two or more hinge functions, which can therefore model the interaction between two or more predictors (x).
In this study, MARS analysis was performed using the “earth” package in R ([39]). To improve predictions and prevent over-fitting, MARS uses a modified form of the “cross-validation method” (GCV - [45]). GCV is an approximation of the error that would be determined by leave-one-out validation and considers both the residual error and the model complexity. Therefore, the optimal model is that yielding the lowest GCV (eqn. 3):
where yi represents the observed values of the dependent variable, n is the number of observations, fm(xi) is the MARS model with M basis functions, xi represents the observed values of the predictors included in the MARS model and pM is the number of parameters of the MARS model.
The importance of the measurement variable was also considered, to take into account whether model information was used or not. Use of the previously mentioned GCV parameter, together with the parameters N of the subsets (Nsub) and the residual sum of squares (RSS), yields reliable results. The Nsub criterion considers the number of model subsets that include the variable, i.e., one subset for each model size from one up to the selected model size (in the final pruned model). The wrapper model utilizes the performance of the algorithm MARS to determine which features should be selected. The subset that produces the highest overall accuracy is deemed the best. For the RSS criterion, the decrease in the RSS is first calculated for each subset relative to the previous subset. For each variable, the decreases are then summed over all subsets that include that variable ([3]).
Three criteria were used to evaluate the model performance: (i) the determination coefficient (R2) as a measure of how well the model fits the training data; (ii) the generalized determination coefficient (GR2), which is based on the GCV statistic and the root mean square error (RMSE) for each model to provide a generalization of the predictive power of the model; and (iii) the common method of k-fold cross-validation (for k = 2 to 10 folds), in which error statistics are calculated across all k trials. Additional information on MARS can be found in Friedman ([18]) and Hastie et al. ([24])
Cross validation was used with the aim of defining a dataset to test the model in the training phase, to minimize problems such as overfitting and to predict how the model will perform with an independent dataset. This provides a good indication of how well the classifier will perform with unseen data and also indicates the degree of variability in the k-fold cross-validation results.
For the purpose of comparison, multiple linear regression (MLR) was also carried out to compare how it performs relative to the MARS technique for modeling stand variables in the study area. MLR is the technique most commonly used in this kind of studies, as it is easy to understand and widely used in most scientific disciplines ([15]). Stepwise selection (forward and backward) was performed to select the most informative variables that were included in the model using the stepAIC function and the exact Akaike’s information criterion (AIC) in the MASS package ([44]). The aim of this procedure was to identify the model with the smallest AIC by removing or adding predictors.
The equations obtained with the MARS technique (R2 and RMSE) were finally used to generate a map of the stand variables by means of the map algebra and conditional tools of the GIS package ArcGIS 10® ([14]).
Results
Tab. 3 shows the results produced by the MLR and MARS techniques for each of the dasometric variables considered in the study. Although MARS generally performed best, MLR yielded better prediction of the H mean variable.
Tab. 3 - Comparison of the best MLR and MARS model predicting seven tree stand attributes based on the coefficient of determination (R2), root mean square error (RMSE) and RMSE percent. (N): the number of trees per plot; (DB mean): mean diameter at 0.30 m (cm); (DBH mean): mean diameter at 1.30 m (cm); (H mean): mean height (m); (CD mean): mean crown diameter (m); (V mean): mean volume (m3); (TV): total volume (m3) per plot; (MLR): MLR technique; (MARS): MARS technique.
| Variable | MLR | MARS | ||||||
|---|---|---|---|---|---|---|---|---|
| Predictors | R 2 | RMSE | %RMSE | Predictors | R 2 | RMSE | %RMSE | |
| N | 5 | 0.18 | 54.20 | 68.15 | 4 | 0.22 | 51.01 | 64.14 |
| DB mean | 6 | 0.33 | 5.47 | 25.56 | 3 | 0.38 | 5.02 | 23.48 |
| DBH mean | 6 | 0.31 | 4.99 | 27.79 | 10 | 0.73 | 3.01 | 16.79 |
| H mean | 7 | 0.36 | 2.65 | 24.20 | 1 | 0.25 | 2.73 | 24.96 |
| CD mean | 6 | 0.32 | 0.78 | 20.31 | 8 | 0.55 | 0.61 | 15.83 |
| V mean | 7 | 0.30 | 0.27 | 64.09 | 7 | 0.57 | 0.20 | 47.39 |
| TV | 5 | 0.40 | 9.39 | 37.59 | 3 | 0.41 | 9.00 | 36.02 |
Tab. 4 shows the results obtained with the MARS models that performed best for estimating the dasometric variables considered in each plot of mixed and uneven aged forest plot in the study area.
Tab. 4 - MARS model selection criteria for dasometric variables considered. (N): number of trees per plot; (DB mean): mean diameter at 0.30 m (cm); (DBH mean): mean diameter at 1.30 m (cm); (H mean): mean height (m); (CD mean): mean crown diameter (m); (V mean): mean volume (m3); (TV): total volume (m3) per plot; (GCV): generalized cross-validation; (RSS): residual sum of squares; (GR2): generalized coefficient of determination.
| Variable | Number of terms |
GCV | RSS | GR 2 |
|---|---|---|---|---|
| N | 5 of 22 | 3273.51 | 215972.50 | 0.04 |
| BD mean | 6 of 34 | 33.55 | 2095.71 | 0.19 |
| DBH mean | 17 of 34 | 26.66 | 754.26 | 0.26 |
| H mean | 2 of 36 | 8.04 | 619.94 | 0.21 |
| CD mean | 9 of 21 | 0.59 | 30.85 | 0.30 |
| V mean | 9 of 34 | 0.06 | 3.24 | 0.34 |
| TV | 4 of 22 | 96.60 | 6722.15 | 0.31 |
According to the selection criteria, the model used to estimate the mean diameter at breast height (1.30 m), mean volume and the mean crown diameter were those that performed best with the training data set (i.e., highest R2 = 0.73, 0.57 and 0.55; GR2 = 0.26, 0.34 and 0.30; and lowest RMSE = 3.01 cm, 0.20 m3 and 0.61 m; 16.79%, 47.39% and 15.83% of the mean variables, respectively). The model used to estimate the total volume per plot also performed reasonably well (R2 = 0.41, GR2 = 0.31, and RMSE = 9.00 m3; 36.02% of the mean total volume per plot). The model used to estimate the number of trees per plot yielded the poorest fit (R2 = 0.22, GR2 = 0.04, with RMSE = 51.01; 64.14% of the mean number of trees per plot) and the model used to estimate the mean height also provided a poor fit to the training data set (R2 = 0.25, GR2 = 0.21 and RMSE = 2.73 m; 24.96% of the mean height). Thus a large difference between GR2 and R2 indicates a severely over-parametrized model, i.e., a model that may show a good fit to the training dataset, but would not be generally applicable.
The predictor variables (spectral bands and indices and topographic variables) used to construct the basic functions can be evaluated after fitting a MARS model to the different dasometric variables. The parameter estimates of the MARS models fitted to the complete database are shown in Tab. 5.
Tab. 5 - Models obtained for the total database by MARS technique. (N): number of trees per plot; (DB mean): mean diameter at base (0.30 m, in cm); (DBH mean): mean diameter at breast height (1.30 m, in cm); (H mean): mean height (m); (CD mean): mean of the crown diameter (m); (V mean): mean volume (m3); (TV): total volume (m3) per plot.
| Variable | MARS models |
|---|---|
| N | +101.0029 - 0.2084·max(0.1479-B5) + 0.19820·max(0.695-FPAR) - 2.5521·max(0,ALB-73) + 11.676·max(0.5.495-SLOPE) |
| BD mean | +23.7517 + 0.0926·max(0.310-B3) - 0.0418·max(0,B3-310) + 0.1064·max(0.283-SAVI) + 0.1814·max(0,SAVI-250) - 0.3544·max(0.97-ALB) |
| DBH mean | +28.5076 - 0.2359·max(0.105-B2) + 0.1826·max(0,B3-310) + 0.1356·max(0,B4-354) + 0.9940·max(0,SAVI-208) - 0.2823·max(SAVI-214) + 1.9544·max(0,SAVI-218) - 2.9222·max(0,ALB-67) + 3.2205·max(0,ALB-70) - 0.2655·max(0,ALB-97) - 0.0347·max(0.2646-DEM) - 0.0319·max(0,DEM-2646) - 7.2031·max(0,CURV+0.463) - 29.5239·max(0,CURV-0) + 41.0845·max(0,PLANCURV-0.107) + 58.5195·max(0,-0.092-PROFCURV) - 1.2622·max(0,WETIND-8.222) |
| H mean | +10.0624 + 0.0950·max(0,SAVI-238) |
| CD mean | +3.4718-0.0220·max(0,B3-348) + 0.0210·max(0,B4-387) + 0.0083·max(0.1247-B5) + 0.0122·max(0,B7-730) + 0.0255·max(0,SAVI-238) - 0.1455·max(0,ALB-97) + 2.100·max(0,-0.185-PROFCURV) - 0.1352·max(0.5.495-SLOPE) |
| V mean | +0.1153 + 0.0061·max(0.280-B3) - 0.0060·max(0,B3-289) + 0.0045·max(0,B4-236) + 0.0174·max(0,SAVI-255) - 0.0123·max(0,DEM-2796) - 0.4713·max(0,CURV-0) + 1.9043·max(0,-0.1851-PROFCURV) - 0.1027·max(0,WETIND-10.51) |
| TV | +29.4140-0.0513·max(0,B7-474) + 0.4461·max(0,SAVI-266) + 0.4821·max(0,ALB-97) |
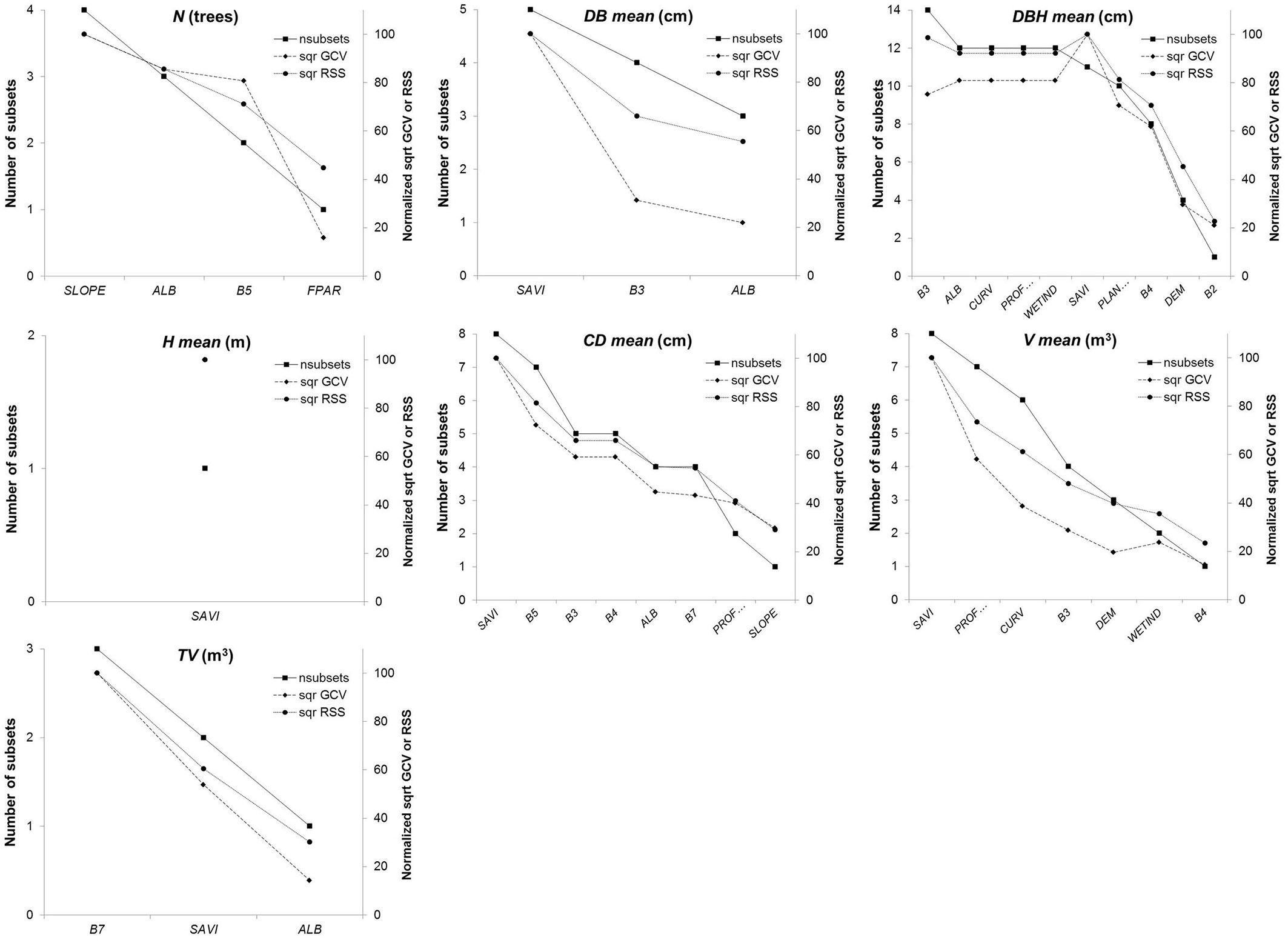
The number of the predictor variables and the percentage contribution to the predictive power of the models varied widely in the models fitted (Fig. 2). For instance, the following variables were the most important (100% of GCV) in some models: slope (SLOPE), for estimating number of trees per plot; soil adjusted vegetation index (SAVI), for estimating mean diameter at base per plot, mean total tree height, mean crown diameter and mean volume; and the green band (B3) and short wave infrared 2 band (B7) for estimating the mean diameter at breast height and the total volume per plot. Likewise, the following variables contributed least to the predictive ability of the models (<25% of GCV): fraction of photosynthetically active radiation (FPAR), for estimating number of trees per plot; albedo (ALB) for estimating the mean diameter at base and the total volume per plot; the blue band (B2), for estimating the mean diameter at breast height, and DEM, wetness index (WETIND) and the red band (B4), for estimating the mean volume.
Fig. 2 - Importance and selection of predictor variables in the multivariate adaptive regression splines (MARS) models for each radiometric correction algorithm considered.
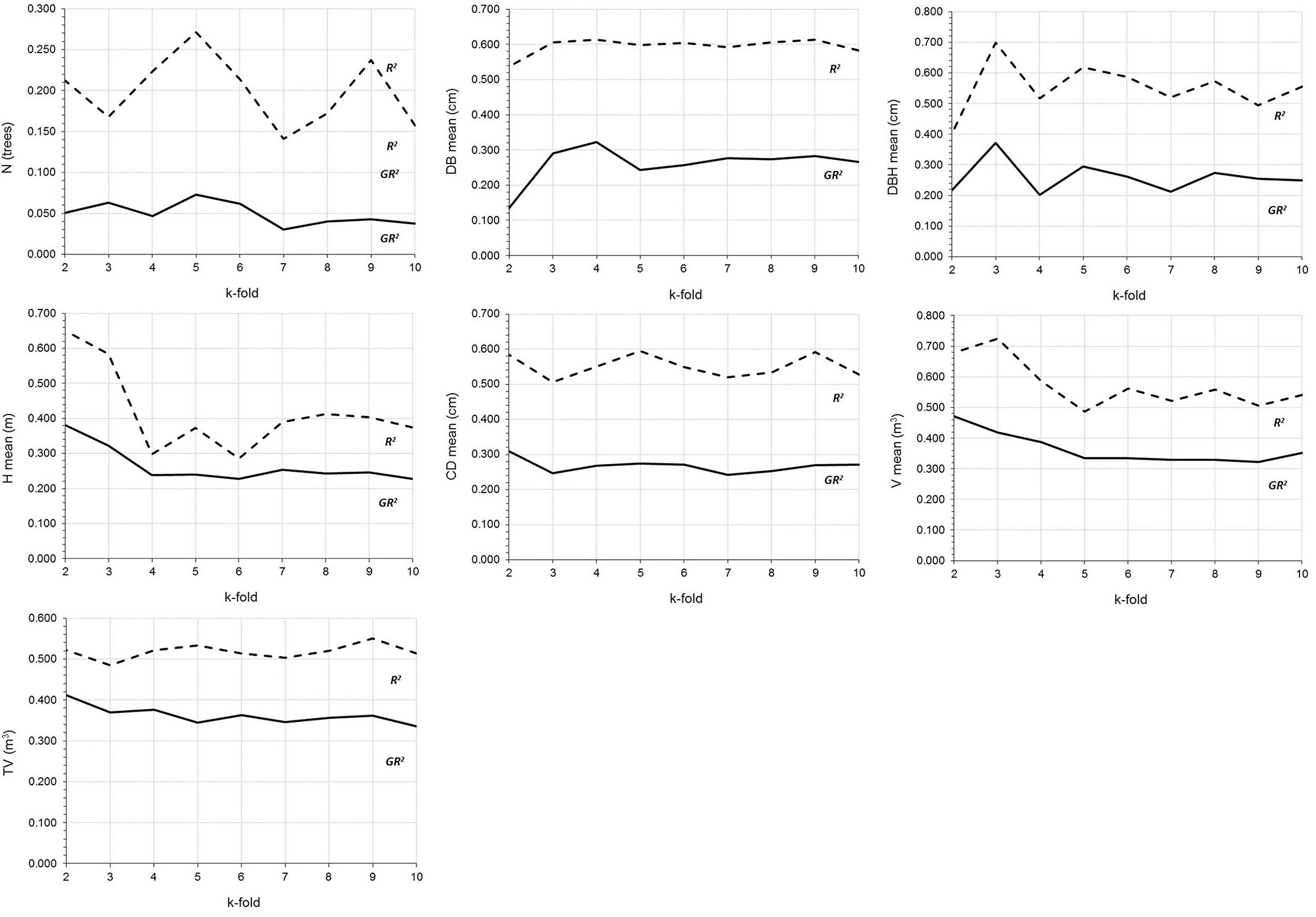
Fig. 3 shows the variation in k-fold cross-validation (k = 2 to 10), which is used to visualize problems such as overfitting. And finally, the spatial distribution of the dasometric variables in the study area obtained by application of the MARS models (Tab. 5) is shown in Fig. 4.
Fig. 3 - Variations in the goodness of fit statistics obtained by applying the cross-validation technique (nfolds = 2-10) to the MARS models.
Fig. 4 - Spatial distribution of the stand variables in the study area, obtained by application of the MARS technique.
Discussion
Predictive modeling is not an exact science ([17]), and model performance can be influenced by the method of statistical analysis, topographical factors (slope, exposure and elevation) and forest structure (proportion of young and mature trees, species and type of silvicultural management). The results obtained in this and other studies ([34], [51], [1]) were based on nonparametric techniques. In this case, the MARS technique yielded significantly more accurate predictions than the MLR excepting the variable H mean as a consequence of the smaller number of predictors (1 of 21) in the MARS model.
However, the use of very high resolution sensors can improve prediction of forest structural parameters by linear regression analysis, as reported by Ozdemir & Karnieli ([36]). These authors used multispectral data (WordView-2) and a stepwise regression technique to predict the number of trees per hectare (R2 = 0.38, RMSE = 109.56 tree ha-1; 28.45%) and total volume per plot (R2 = 0.42, RMSE = 27.18 m3 ha-1; 44.20%) in a plantation forest in Israel.
Trotter et al. ([43]) obtained high goodness-of-fit values (R2 ≥ 0.85 and RMSE = 39.00 m3 ha-1) for band 4, and for bands 3 and 4 of Landsat TM satellite images for estimating timber volume by simple and multiple linear regression methods, respectively. In a study monitoring growth of a young forest plantation in UK, they used generalized linear models (GLM) with logarithmic links and normal errors, and obtained higher values (R2 = 0.85 and RMSE = 0.88 m; 28.38%) for the mean height, and lower values for the diameter at breast height (R2 = 0.36 and RMSE = 2.15 cm; 27.24%) and for density (R2 = 0.03 and RMSE = 3.260.59 tree ha-1; 98.62%) than those obtained in the present study. The differences in the results can be explained by the more heterogeneous conditions of the native vegetation in the present study area and, in the case of height, the higher R2 values obtained in UK may also be related to the larger latitude in this country, which implies longer shadows at the time of the Landsat overpass, making it easier to estimate tree heights ([11]). In a study modeling forest stand structure attributes by multivariate regression and discriminant function analysis, Hall et al. ([23]) obtained higher error values for height and crown cover (R2 = 0.57 and 0.65, and RMSE = 12.0 and 2.8 m, respectively). Coulston et al. ([9]) estimated crown cover in forests in Utah and Michigan (USA) by using a beta regression model and the random forest algorithm, and obtained also high error values (R2 = 0.65 and 0.69 and RMSE = 0.87 and 0.89 m, respectively).
Cruz-Leyva et al. ([10]) modeled even-aged Pinus patula and P. teocote forest stand variables in Hidalgo, Mexico by GIS variables and reflectance data derived from a multispectral SPOT 5 image and multiple linear regression. The volume was significantly related to tree crown cover, leaf area index (LAI), slope, elevation, mean annual temperature, maximum temperature of warmest month, mean annual precipitation, and precipitation of the wettest quarter (R2 = 0.72 and 0.88, p < 0.001).
Li et al. ([29]) used stepwise linear regression and regression tree analysis, together with cross validation methods, to estimate height in young forests and obtained the following values for the first and second modeling techniques, respectively: R2 = 0.15 and 0.19 and RMSD (root mean square of the difference) = 10.32 and 6.07 (m) for the first group of variables by combining bands 1-5 and 7 to obtain the integrated forest index (IFI), a measure of the probability that a pixel corresponds to forest, the normalized difference vegetation index (NDVI) and the normalized burn ratio index (NBRI). The same authors obtained R2 = 0.88 and 0.89 and RMSD = 2.42 and 2.13 (m) for the second group of variables (age since disturbance, derived from Vegetation Change Tracker [VCT] and Landsat time series stacks [LTSS] disturbance year map), and R2 = 0.69 and 0.68 with RMSD =3.85 and 3.73 (m) successively for the third group of variables (combining accumulated indexes: IFI, NDVI and NBRI).
The null contribution of the NDVI (Fig. 2) can be attributed to the significant association between this index and both the leaf area index and the fraction of photosynthetically active radiation intercepted ([28]). The values of these variables are low in winter, which is when the satellite image was captured and the field sampling was carried out for the present study.
Some estimates are difficult to compare, because of differences in the sources of data, estimation methods used, period of data compilation and large differences between the study areas ([50]).
The top performing model (R2) was that used to estimate the mean diameter at breast height, probably because this model included the largest number of independent variables (Tab. 4), indicating problems of overfitting (GR2) in the training data set (Fig. 3). The remaining unexplained variance in the spatial patterns may be related to the high heterogeneity of the dependent variables ([20]), due to the uneven-aged and tree species-rich structure of the Pueblo Nuevo forests in Durango. We therefore recommend increasing the number of observations in order to decrease the possibility of occurrence of this effect.
Considering the advantages and limitations of different remote sensing images, the medium-resolution (pixel size, 30 m) Landsat series is one of the most widely used for estimating dasometric variables ([2], [38], [12], [52]). The advantages of using the Landsat series are that numerous historical spatiotemporal archives are available and that the sensor is cheaper and more accessible than high resolution sensors, particularly for analysis of large areas ([48]).
Conclusions
We conclude that the spectral bands of the Lansat-8 OLI sensor can be used to estimate four of the seven stand variables (mean diameter at breast height, mean crown diameter, mean volume and total volume per plot) in the study region. Furthermore, the inclusion of aggregated values of vegetation indexes and terrain variables derived from the DEM contributed significantly to increasing the the goodness-of-fit of the models.
Multivariate adaptive regression splines (MARS) models are more flexible than linear regression models. Application of the MARS technique facilitated handling and interpretation of large amounts of data representing complex structures. The predictors thus obtained for the study area were accurate and the method proved suitable for modeling a large number of predictive variables.
References
Online | Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Authors’ Info
Authors’ Affiliation
José C Hernández-Díaz
Christian Wehenkel
Instituto de Silvicultura e Industria de la Madera. Universidad Juárez del Estado de Durango, Bvld del Guadiana 501, Fracc. Ciudad Universitaria, C.P. 34120 Durango (México)
Pablito M López-Serrano
Doctorado Institucional en Ciencias Agropecuarias y Forestales. Universidad Juárez de Estado de Durango (UJED)
GEOcentro UNIGIS-USFQ. Universidad de San Francisco de Quito, Cumbaya (Ecuador)
Corresponding author
Paper Info
Citation
López-Sánchez CA, García-Ramírez P, Resl R, Hernández-Díaz JC, López-Serrano PM, Wehenkel C (2017). Modelling dasometric attributes of mixed and uneven-aged forests using Landsat-8 OLI spectral data in the Sierra Madre Occidental, Mexico. iForest 10: 288-295. - doi: 10.3832/ifor1891-009
Academic Editor
Alessandro Montaghi
Paper history
Received: Oct 01, 2015
Accepted: Oct 12, 2016
First online: Feb 11, 2017
Publication Date: Feb 28, 2017
Publication Time: 4.07 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2017
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 51920
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 42141
Abstract Page Views: 3915
PDF Downloads: 4627
Citation/Reference Downloads: 25
XML Downloads: 1212
Web Metrics
Days since publication: 3262
Overall contacts: 51920
Avg. contacts per week: 111.42
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2017): 11
Average cites per year: 1.22
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Estimating biomass of mixed and uneven-aged forests using spectral data and a hybrid model combining regression trees and linear models
vol. 9, pp. 226-234 (online: 21 September 2015)
Review Papers
Remote sensing-supported vegetation parameters for regional climate models: a brief review
vol. 3, pp. 98-101 (online: 15 July 2010)
Review Papers
Accuracy of determining specific parameters of the urban forest using remote sensing
vol. 12, pp. 498-510 (online: 02 December 2019)
Review Papers
Remote sensing of selective logging in tropical forests: current state and future directions
vol. 13, pp. 286-300 (online: 10 July 2020)
Technical Reports
Detecting tree water deficit by very low altitude remote sensing
vol. 10, pp. 215-219 (online: 11 February 2017)
Research Articles
Assessing water quality by remote sensing in small lakes: the case study of Monticchio lakes in southern Italy
vol. 2, pp. 154-161 (online: 30 July 2009)
Research Articles
Classification of xeric scrub forest species using machine learning and optical and LiDAR drone data capture
vol. 18, pp. 357-365 (online: 07 December 2025)
Research Articles
Afforestation monitoring through automatic analysis of 36-years Landsat Best Available Composites
vol. 15, pp. 220-228 (online: 12 July 2022)
Technical Reports
Remote sensing of american maple in alluvial forests: a case study in an island complex of the Loire valley (France)
vol. 13, pp. 409-416 (online: 16 September 2020)
Review Papers
Remote sensing support for post fire forest management
vol. 1, pp. 6-12 (online: 28 February 2008)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords