Estimating biomass of mixed and uneven-aged forests using spectral data and a hybrid model combining regression trees and linear models
iForest - Biogeosciences and Forestry, Volume 9, Issue 2, Pages 226-234 (2015)
doi: https://doi.org/10.3832/ifor1504-008
Published: Sep 21, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
The Sierra Madre Occidental mountain range (Durango, Mexico) is of great ecological interest because of the high degree of environmental heterogeneity in the area. The objective of the present study was to estimate the biomass of mixed and uneven-aged forests in the Sierra Madre Occidental by using Landsat-5 TM spectral data and forest inventory data. We used the ATCOR3® atmospheric and topographic correction module to convert remotely sensed imagery digital signals to surface reflectance values. The usual approach of modeling stand variables by using multiple linear regression was compared with a hybrid model developed in two steps: in the first step a regression tree was used to obtain an initial classification of homogeneous biomass groups, and multiple linear regression models were then fitted to each node of the pruned regression tree. Cross-validation of the hybrid model explained 72.96% of the observed stand biomass variation, with a reduction in the RMSE of 25.47% with respect to the estimates yielded by the linear model fitted to the complete database. The most important variables for the binary classification process in the regression tree were the albedo, the corrected readings of the short-wave infrared band of the satellite (2.08-2.35 µm) and the topographic moisture index. We used the model output to construct a map for estimating biomass in the study area, which yielded values of between 51 and 235 Mg ha-1. The use of regression trees in combination with stepwise regression of corrected satellite imagery proved a reliable method for estimating forest biomass.
Keywords
Regression Trees, Stepwise Regression, Remote Sensing, ATCOR3, Terrain Features, Image Texture
Introduction
The Sierra Madre Occidental is considered an area of special ecological interest because of the high levels of biodiversity, which are attributed to diverse physiographic and climatic conditions ([11]). The area is also important because of the presence of some of the most important commercial species of pine and oak in Mexican ecosystems ([66]).
Quantification of forest biomass and carbon sequestration is a relevant issue in the management of these forest stands. Reliable information is required for accurate biomass estimation, which should also take into account variable external factors that can be modeled, e.g., climate change ([35], [64], [68]). However, given the diversity of environmental, topographical and biophysical conditions in forest ecosystems in different locations, there is no universal, transferable technique for estimating biomass ([37], [18], [45], [14]).
In general, forest biomass can be measured directly (destructive analysis) or it can be estimated indirectly ([9]). The direct method is usually accurate, but it is expensive and time-consuming and can only be used in small areas ([38], [76], [72]). These difficulties have largely been resolved by the appearance and further development of quantitative satellite systems and aerial remote sensing, together with the development of parametric and nonparametric statistical methods for modeling variables of interest. The stand variables usually measured in traditional forest inventories can now be estimated faster, at lower cost and over larger areas ([44]). The application of spatial technologies has allowed estimation of biomass in different ecosystems ([52], [21], [28], [1]).
Pre-processing of satellite imagery is important for improving the quality and interpretation of data. Forest ecosystems generally cover rough terrain where the topographic conditions lead to variations in reflectance values because of the position of the sun ([49], [61], [60]). Thus, the quality of the final product largely depends on accurate calibration of the sensors and on radiometric correction to minimize distortion and atmospheric effects ([42]). In this respect, the use of atmospheric and topographic correction is therefore essential to counteract such effects, and digital elevation model (DEM) parameters such as slope, orientation, shadows cast, sky view and altitude can be used for such purposes ([4], [60]). These primary parameters, together with biophysical parameters such as vegetation indexes ([24]) and indexes derived by the analysis of the image texture (by quantification of the spatial variation in grey tones using a grey level co-occurrence matrix - GLCM), are very useful for identifying areas or objects of interest in the image ([27], [7]). They can also be combined with terrain parameters to model vegetation characteristics ([45], [36], [15]), as well as to describe hydrological, geomorphological and ecological processes ([50], [73]).
One of the methods most commonly used for this purpose is the classification and regression trees method, initially proposed by Breiman et al. ([8]). This is a non-parametric, multivariate, supervised, inductive learning method that basically searches for classification and prediction rules by recursive partitioning. In this technique, a series of binary combinations (yes, no) expressed in terms of a single independent variable is used to identify certain profiles and vectors that enable description of the individual parameters under study ([31]).
The objective of the present study was to model the forest biomass in mixed and uneven-aged forests in the Sierra Madre Occidental (Mexico) by using remote sensing Landsat-5 TM imagery, terrain parameters and forest inventory data obtained from a network of permanent plots sampled in a traditional (ground based) survey. Two different approaches were compared: the usual modeling method of fitting a linear relationship to stand biomass and site variables obtained from remote sensing images, and a new approach consisting of a hybrid model combining regression trees and linear models for the final tree nodes. As far as we know, this is the first time this hybrid approach has been used to model stand biomass with remote sensing data.
Material and methods
Study area
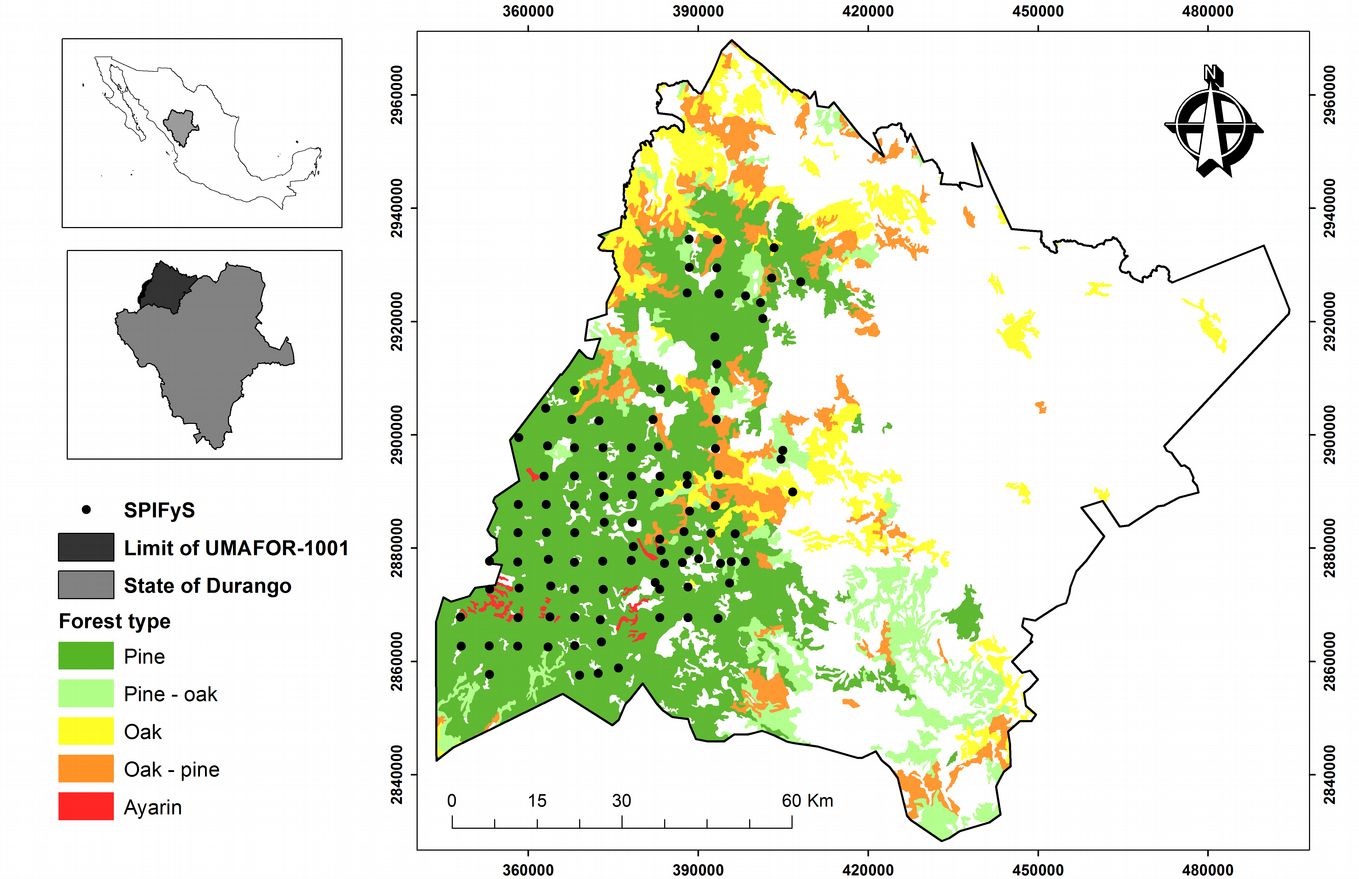
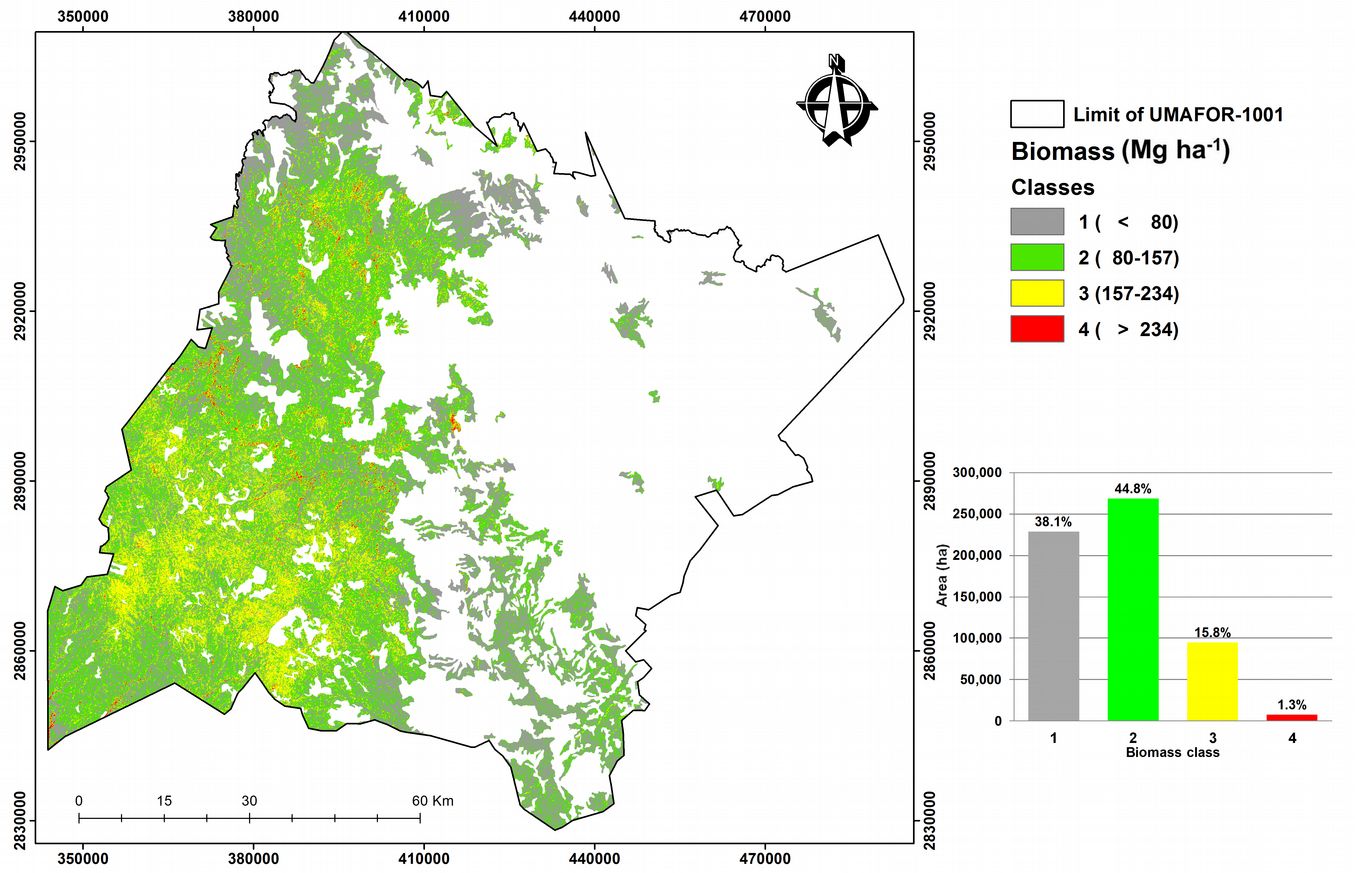
The study area is located in the UMAFOR-1001 (Unidad de Manejo Forestal Regional or regional forest management unit) in the Sierra Madre Occidental, in the north of the state of Durango (Mexico), and covers an area of 1 142 916 ha (Fig. 1). The vegetation comprises pine, oak, Douglas fir, pine-oak and oak-pine forest, according to the description in the Land Use and Vegeta-tion Cover Chart, scale 1:250.000, Series V ([33]).
Field data
A network of 99 permanent sampling plots was established during the winter of 2011, following the method described by Corral-Rivas et al. ([13]). The plots were located by systematic sampling (with some exceptions to avoid non forested areas) with a grid of equidistant points separated by three to five kilometers, depending on the orography of the study area. In each plot (50 × 50 meters), the tree species were recorded and the diameter at breast height > 7.5 cm and total height (m) of all standing trees were measured.
Species-specific statistical models developed by Vargas-Larreta ([71]) were used to estimate individual (at tree level) aboveground biomass. The goodness of fit for such statistical models ranged from 0.87 to 0.99 (R2), and the root mean square error (RMSE) varied from 22.8 to 95.2 kg. Once the tree aboveground biomass was estimated, all values from each sampling plot were summed and expressed on a per hectare basis. Summary statistics including number of observations, mean, standard deviation, minimum, and maximum values of the main stand variables are shown in Tab. 1.
Tab. 1 - Statistics of the main stand variables. Dominant height was calculated as the mean height of the 100 thickest trees per hectare.
| Variable | Mean | Standard deviation |
Minimum value |
Maximum value |
|---|---|---|---|---|
| Number of stems per ha | 655.47 | 322.25 | 224.00 | 2264.00 |
| Stand basal area (m2 ha-1) | 20.30 | 6.42 | 8.22 | 41.12 |
| Dominant height (m) | 14.62 | 3.72 | 6.87 | 24.81 |
| Stand biomass (Mg ha-1) | 89.03 | 43.45 | 2.70 | 234.03 |
Datasets
Source of spectral data
Three Landsat-5 TM (Thematic Mapper) satellite images (path/row: 31/42, 32/41 and 32/42), obtained in April and May 2011 and covering the entire study area, were examined (available from the US Geological Service webpage - ⇒ http://glovis.usgs.gov/). The available images are subjected to cubic convolution geometric correction for discrete data (level L1T), with a RMSE of the geometric residuals lower than 1 pixel, and they are therefore suitable for image processing ([39]).
Landsat-5 TM data have spatial resolution of 30 m with a 16 day revisit period. The swath width is 185 km with seven spectral bands in the following wavelength regions of the electromagnetic spectrum: blue (0.45-0.52 µm), green (0.52-0.60 µm), red (0.63-0.69 µm), near infrared (0.78-0.89 µm), short-wave infrared (1.55-1.75 µm) and short-wave infrared (2.08-2.35 µm). These wavelength regions correspond respectively to bands 1, 2, 3, 4, 5 and 7 of the Landsat-5 TM satellite ([54]). Given its thermal characteristics, band 6 was not used in the present study.
Atmospheric and topographic correction (ATCOR3®)
The satellite images were subjected to radiometrical, atmospherical and topographical correction using the ATCOR3® module, regarded as particularly suitable for mountainous zones ([23]) and implemented in the ERDAS® IMAGINE® 2013 software ([16]). After correction, the original image digital levels (DL) were converted to ground reflectance values for each band. A number of vegetation indexes and other derived parameters (Tab. 2) were computed from the atmospherically and topographically corrected image bands and then included in the biomass estimation models for their evaluation as possible regressor variables. Vegetation indexes are regarded as good indicators of vegetation cover “greenness” (understood as a combination of attributes such as leaf chlorophyll content, leaf area, canopy cover and structure - [25]) and are good indicators of vegetation canopy biomass. Hence, the Normalized Difference Vegetation Index ([63]) and Soil Adjusted Soil Vegetation Index ([32]) were included as indexes correlated with green biomass content, with the former being particularly suited for scattered vegetation land cover. The Leaf Area Index ([5]) derived from NDVI was also included as a good indicator of green biomass. Albedo ([2]), photosynthetically active radiation ([3]) and absorbed shortwave solar radiation ([10]) were also included as comprehensive indicators of the interaction between land cover and solar radiation in the visible and near-infrared regions of the electromagnetic spectrum.
Tab. 2 - Vegetation indexes analyzed in the present study. (NIR): Near-infrared band (0.83 μm); (RED): Red band (0.63 μm); (ρ): Reflectance; (1-ρ(λ)): Absorbed part of radiation; (Eg(λ)): the global (direct plus diffuse) solar flux on the ground; (C): Constant value 0.8; (A): Constant value 1; (B): Constant value 0.4; (int0.3-2.5μm): extrapolation for region of the 0.3-2.5 μm (bands) of most satellite sensors; (dλ): adjustable parameter used to derive direct albedo on solar zenith angle.
| Vegetation index | Definition | Author |
|---|---|---|
| Normalized Difference Vegetation Index | NDVI=(NIR-RED)/(NIR+RED) | Rouse et al. ([63]) |
| Soil Adjusted Soil Vegetation Index | SAVI=[(ρNIR-ρRED)·1.5]/[(ρNIR+ ρRED)+0.5] | Huete ([32]) |
| Modified Soil-adjusted Vegetation Index | MSAVI2=[2· NIR+1-√[(2· NIR+1)2 -8· (NIR-RED)]]/2 | Qi et al. ([58]) |
| Leaf Area Index | LAI=-(1/0.6)ln[(0.6-NDVI)/0.78] | Baret & Guyot ([5]) |
| Albedo | a=int0.3-2.5μm [ρ(λ)d(λ)] / int0.3-2.5μm (dλ) | Asrar ([2]) |
| Fraction of Photosynthetically Active Radiation | FPAR= C· 1-A exp(-B· LAI)] | Asrar et al. ([3]) |
| Absorbed Shortwave Solar Radiation | Rsolar=int0.3-2.5μm [1-ρ(λ) Eg(λ) dλ] | Brutsaert ([10]) |
The ATCOR3® module ([23]) first calculates the radiance at sensor level (Wsr-1 m-2) from the image pixels DL. Several input parameters were required for this calculation and were retrieved from the image metadata (header file): date of acquisition, scale factors, geometry (solar zenith angle and solar azimuth) and other information about the sensor calibration file (“gain and bias”). Other parameters were adjusted by taking into account particularities of the input datasets and the conditions of the imagery dates, e.g., visibility (35 km), pixel size of the DEM (15 m), aerosol type (rural), among others. As the image was cloudless and no suitable water vapor bands were available, dehazing/ cloud removal and atmospheric water retrieval settings were retained as “default”, which, in this case, is recommended by the ATCOR3® User Manual ([23]).
As a prior requisite for application of the ATCOR3® module, three topographic parameters (namely slope, orientation, skyview and shadows cast - [60]) were computed from a DEM of the study area with a spatial resolution of 15 m ([34]). Prior to these calculations, a low pass filter with a 5×5 moving window was applied to the original DEM in order to reduce the banding effects present in the original file.
After radiometric correction, the three scenes corresponding to the study area were mosaicked using the ERDAS® IMAGINE® 2013 software ([16]).
Texture parameters
With the aim of including information that combines the spatial and spectral domain of the remote sensed imagery in the biomass estimation models, the following texture parameters were calculated from the NDVI image based on grey level co-occurrence matrices (Tab. 3): homogeneity, contrast, dissimilarity, mean, standard deviation, entropy, second order angular moment and correlation ([27]). Calculations were done at three different analysis scales, corresponding to window sizes of 3×3, 5×5 and 7×7 pixels, respectively. The original NDVI image values were resampled to a grey level depth of 256 (8 bits) to reduce computational costs ([27]). This procedure was carried out using the software package PCI Geomatica 2013® ([57]).
Tab. 3 - Additional variables for biomass modelling. (N): number of grey levels; (P): normalized symmetric GLCM of dimension N×N; (V): vector difference normalized grey level of dimension N; P(i, j): matrix of co-occurrence normalized, so that Σ(i,j=0;N-1) Σ(i,j=0;N-1) P(i-j); V(k): normalized grey level difference vector Σ(i,j=0;N-1)Σ(i,j=0;N-1)P(i-j)| i-j | = k; (Z): Average elevation; (R): Point radio altitude units; (As): Drainage area specified; (tan(β)): Local slope angle; (VA): Variance; (ME): Mean. D, F, G and H were derived according to equation of Zevenbergen & Thorne ([74]).
| Group variable | Variable | Formula | Reference |
|---|---|---|---|
| Texture (NDVI) | Homogeneity (HO) | HO=Σ(i,j=0;N-1) i[Pi,j /1+(i-j)2] | Haralick et al. ([27]) |
| Contrast (CO) | CO=Σ(i,j=0;N-1) i Pi,j (i-j)2 | ||
| Dissimilarity (DI) | DI=Σ(i,j=0;N-1) i Pi,j (i-j) | ||
| Mean (ME) | ME=Σ(i,j=0;N-1) i Pi,j | ||
| Standard Deviation (Sdt) | Sdt=√VA | ||
| Entropy (EN) | EN=Σ(i,j=0;N-1) i Pi,j [-ln(i)-Pi,j] | ||
| Angular Second Moment (ASM) | ASM=Σ(i,j=0;N-1) i P2i,j | ||
| Correlation (CR) | CR=Σ(i,j=0;N-1) i Pi,j [(i-ME)(j-ME)/√(VAi VAj)] | ||
| Terrain (DEM) | Elevation | Digital Elevation Model | - |
| Slope (β) | β= arctan(G2 + H2)1/2 | - | |
| Transformed Aspect (Trasp) | Trasp=1-cos[(π /180)(α- 30)]/2 | Roberts & Cooper ([62]) | |
| Terrain Shape Índex (TSI) | TSI=Z/R | McNab ([46]) | |
| Wetness Index (WI) | W= ln[As/tan(β)] | Moore & Nieber ([50]) | |
| Profile curvature (Ø) | Ø=-2[DG2+EH2+FGH]/(G2+H2) | Wilson & Gallant ([73]) | |
| Plan curvature (ω) | ω=2[DH2+EG2+FGH]/(G2+H2) | ||
| Curvature (x) | x= ω - Ø |
Terrain variables
Terrain variables are directly related to forest species composition, tree height growth, and other forest stand variables, and enable these to be modeled ([46], [62]). Therefore, first and second order terrain parameters (Tab. 3) were derived from the 5×5 low pass filtered DEM ([34]) and included as candidate variables in the models. The selected first order terrain parameters were elevation, slope, transformed aspect, profile curvature, plan curvature and curvature, while second order terrain parameters were terrain shape index and wetness index. These parameters are potentially related to key features for forest stand development, such as overall climate characteristics, insolation, evapotranspiration, run-off, infiltration, wind exposure and site productivity. Some of these terrain features are widely used in hydrological, geomorphological and ecological studies ([73]), whereas others are used more specifically for vegetation and forest assessment ([46], [62]).
Dataset integration
The sample plots were geopositioned with the aim of extracting the pixel value average with an associated buffer of 25 m for each potential predictor. This extraction was carried out using the statistical software R ([59]) and the “raster” package. Finally, a database was constructed with the mean biomass values for each plot: the corrected bands of the Landsat-5 TM sensor (6 bands: 1, 2, 3, 4, 5 and 7), the vegetation indexes (6 indexes), the texture variables derived from the Normalized Difference Vegetation Index (NDVI - 24 variables), and the terrain variables derived from the DEM (8 variables).
Models fitted
The biomass of the sample plots was estimated using two different methods. In the first, the ordinary least squares (OLS) method was used to fit a linear model to estimate stand biomass. The best set of independent variables was selected by using the stepwise variables selection method. The second method consisted of a two-step hybrid approach. In the first step, a regression tree was used to classify the sample plots in homogeneous groups according to their biomass values by a binary rule-based method. In the second step, the ordinary least square method was used to fit linear models to estimate stand biomass for each group by using the stepwise variable selection method to select the best set of independent variables. In both methods, the 45 spectral, texture and terrain variables were taken into account as possible independent variables.
Regression tree analysis (CaRT) is a non-parametric technique for the sequential partitioning of a data set composed of a continuous response variable and any number of potential continuous or categorical predictor variables, by using dichotomous criteria ([8]). After each split, the algorithm identifies the predictor variable that provides the most effective binary separation of the range in the response variable. As a result, predictor variables can be used more than once. The regression tree analysis was performed using the “rpart” package in R ([70], [59]). This approach partitions the data set sequentially, considering two-way splits at each tree node. The best split at each node t is the split that maximizes the following quantity (eqn. 1):
where PL and PR are the proportions of sample plots that fall respectively to the left and right branch of node t; Err(tL) and Err(tR) are the error of the left and right branches; Err(t) is the mean square error at node t given by (eqn. 2):
and (bar)yt is the stand biomass assigned to node t, calculated as the mean of the stand biomass of all the sample plots in node t.
Instead of applying stopping rules, a sequence of sub-trees was generated by growing a large tree and pruning it back until only the root node was left. The error of each sub-tree was then estimated by cross-validation, and the sub-tree with the lowest error was chosen by analyzing the values of the complexity parameter defined by Breiman et al. ([8]).
Once the sample plots of each final node were obtained, a multiple linear model was fitted to estimate the stand biomass, using stepwise selection methods to select the best set of independent variables, with the SAS/STAT® software package ([67]). Two criteria were considered for the evaluation of model performances: the coefficient of determination (R2) and the RMSE. The expressions of these statistics are summarized as follows (eqn. 3, eqn. 4):
where yi, (hat)yi and (bar)y are the observed, estimated and mean biomass values, n is the total number of observations used to fit the model, and p is the number of model parameters.
The main problem associated with such multiple linear models is the multicollinearity. This refers to the existence of high correlations between certain independent variables representing or measuring similar phenomena. Although the least-squares estimates of regression coefficients remain unbiased and consistent under the presence of multicollinearity, they are no longer efficient ([53]). This may seriously affect the standard errors of the coefficients, thus invalidating statistical tests and confidence intervals ([55]). One of the main sources of multicollinearity is the use of overfitted models that include several polynomial and cross-product terms. To evaluate the presence of multicollinearity between variables in the models, the condition number, defined as the square root of the ratio of the largest to the smallest eigenvalue of the correlation matrix, was used. According to Belsey ([6]), condition numbers between 5 and 10 indicate that multicollinearity will not be a major problem, while those in the range 30-100 indicate moderate multicollinearity and those in the range 1000-3000 indicate severe multicollinearity. Therefore, independent variables with condition numbers higher than 30 were not used in the models.
Finally, since the quality of fit does not necessarily reflect its predictive performance ([53]), an assessment of the validity of the models with an independent dataset is recommended ([40]). Due to the difficulties associated with collecting such data, cross-validation was applied in this study. Validation of the model fitted to the complete database (method 1) and of the model of each final node was thus based on the values of coefficient of determination and root mean square error, using the predicted residual sum of squares (PRESS), i.e., each sample plot is removed in turn and the model is refitted using the remaining sample plots. The out-of-sample predicted value is calculated for the omitted sample plot in each case, and the PRESS statistic is calculated as the sum of the squares of all the resulting prediction errors.
The equations obtained with the best method were finally used to generate a map of biomass by means of the map algebra and conditional tools of the GIS package ArcGIS 10® ([17]) from the vector vegetation layer ([33]).
Results
The parameter estimates of the linear model fitted to the complete database using OLS and the stepwise variables selection method is shown in Tab. 4. All the parameters were significant at a 5% level, and up to 5 independent variables were included in the model without generating multicollinearity problems. The model explained 58.83% of the observed stand biomass variability with a RMSE of 27.88 Mg ha-1 (31.32% of the mean stand biomass). Based on the results of cross-validation, the model explained 51.33% of the total observed variation in stand biomass with a RMSE value of 30.31 Mg ha-1 (34.04% of the mean stand biomass).
Tab. 4 - Model obtained for the total database by OLS with stepwise selection of independent variables (*): RMSE expressed as a percentage of mean stand biomass.
| Parameter | Estimate | Standard error | OLS | Cross-validation | ||
|---|---|---|---|---|---|---|
| RMSE (Mg ha-1) |
R 2 | RMSE (Mg ha-1) |
R 2 | |||
| Intercept | 572.4939 | 172.2304 | 27.88 (31.32%)* | 0.5833 | 30.31 (34.04%)* | 0.5133 |
| SAVI | -0.3673 | 0.1566 | ||||
| Band 7 | -2.7166 | 0.6893 | ||||
| Abs. Shortw. solar rad. | 0.0797 | 0.0245 | ||||
| LAI | 0.0166 | 0.0037 | ||||
| Modified SAVI | -2215.8205 | 717.3984 | ||||
| NDVI | 2072.8881 | 628.6811 | ||||
| Wetness index | 3.4027 | 1.5666 | ||||
| Contrast 7×7 | 0.2073 | 0.0926 | ||||
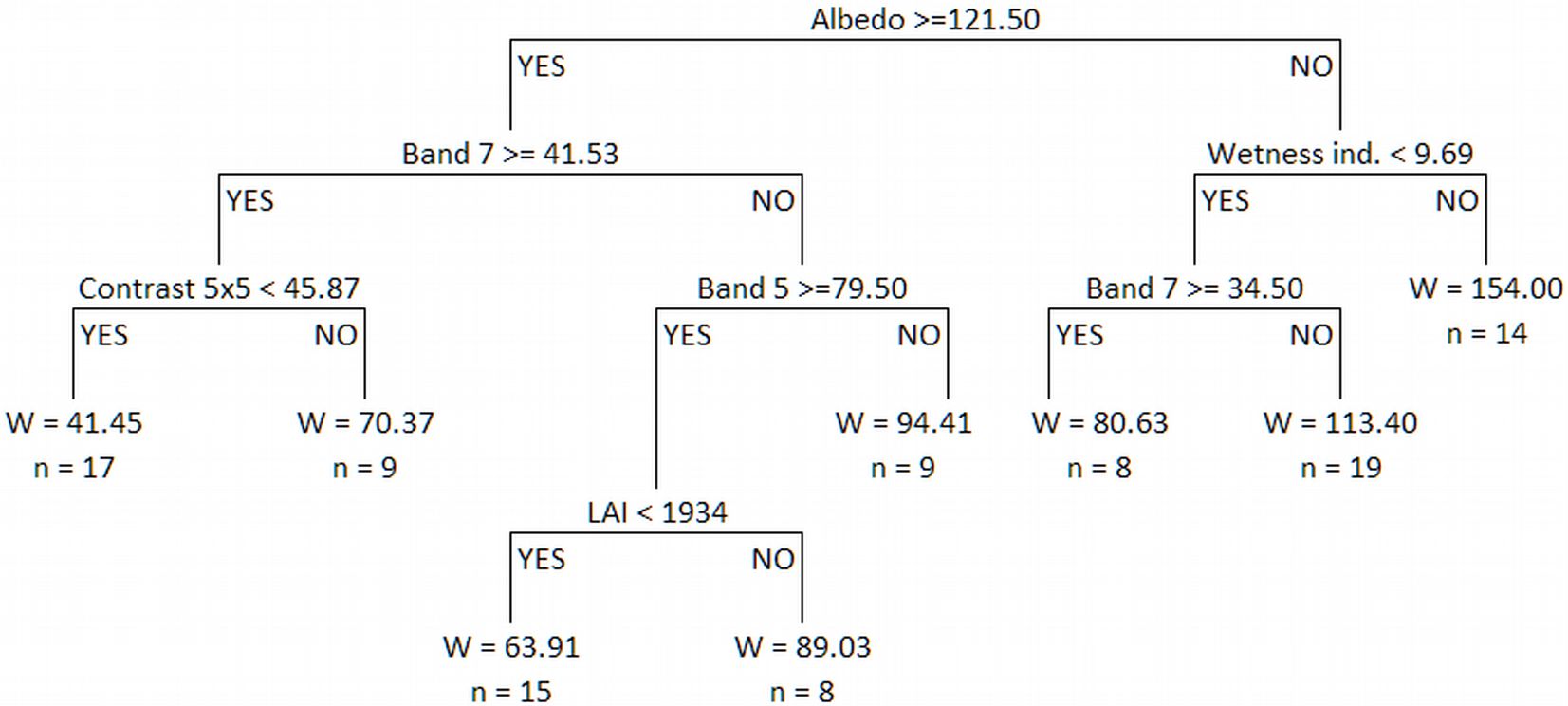
The regression tree shown in Fig. 2 was generated in the first step of the second methods. This tree has a root node that contains all 99 sample plots with an assigned mean biomass value of 89.03 Mg ha-1. The limiting value of 121.5, for the variable albedo, divided these samples into two groups of plots. Each subgroup was then sequentially divided by the limiting values of the variables band 7, band 5, LAI, contrast texture with a 5×5 window and wetness index.
Fig. 2 - Classification tree obtained by the regression tree method. n is the number of sample plots in each node and W is the biomass value for each node (Mg ha-1).
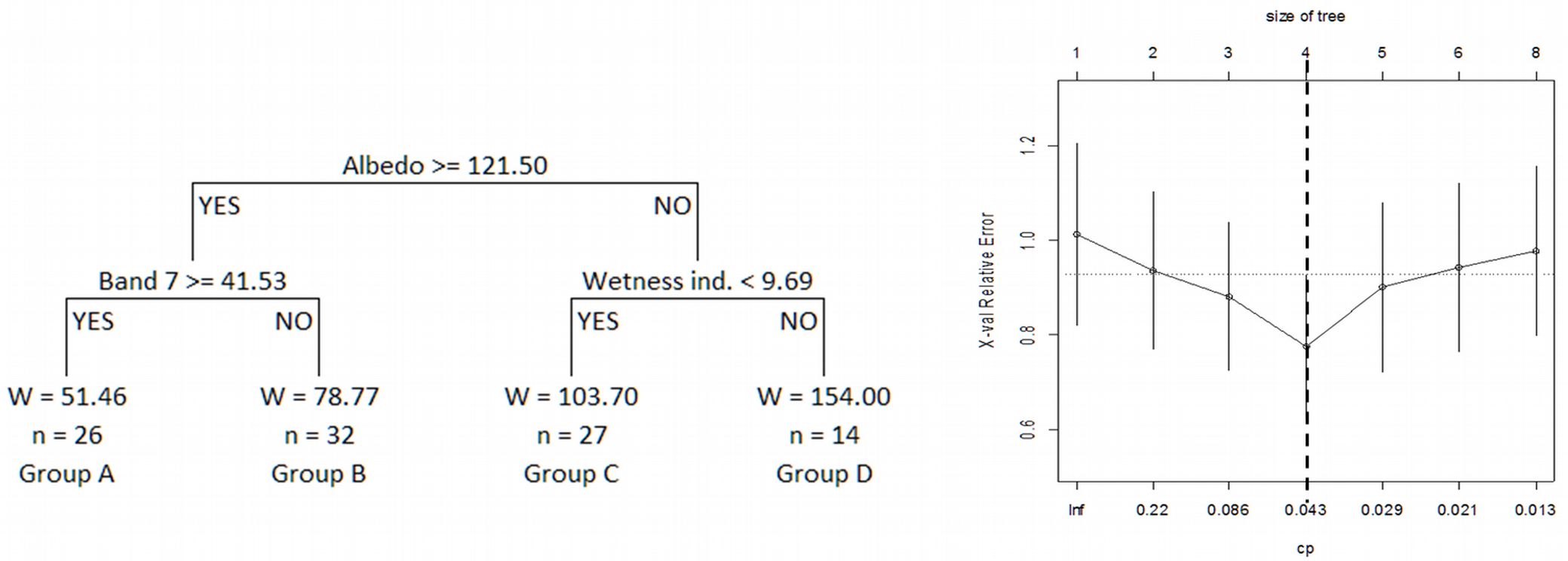
However, the problem with the regression trees method is that it tends to overfit the data, and therefore the most general model may not be obtained when a new set of independent data is used ([8]). These authors suggested that once the tree is constructed, it should be exhaustively pruned by successively removal of branches or terminal nodes that contribute little to explaining the response variable, to yield an appropriately-sized tree. The mean value of the complexity parameter (CP) defined by Breiman et al. ([8]) and obtained by cross-validation, was used in this case to select the number of branches on the final tree, and the result is shown in Fig. 3 (the number of tree input variables was reduced to three, namely albedo, band 7 and wetness index).
Fig. 3 - Classification tree obtained by pruning the regression tree (left) and plot of the relationships between the cost-complexity parameter (CP), the cross validation error (x-val Relative Error) and tree size (number of nodes). The dashed vertical line represents the maximum number of nodes (corresponding cost-complexity parameter) for which the cross validation error is greater than the standard error (right).
Direct application of the regression tree to the data from the 99 permanent sample plots used in this study resulted in 56.76% of the observed variability in stand biomass being explained by the model, with an RMSE value of 28.57 Mg ha-1 (32.09% of the mean stand biomass). Once the four groups shown in Fig. 3 were obtained from the tree, linear models were fitted to each. The parameter estimates, their standard errors and the goodness-of-fit statistics obtained by cross-validation are shown in Tab. 5.
Tab. 5 - Model obtained for the final nodes of the regression tree by OLS and stepwise selection of independent variables (*): RMSE expressed as a percentage of mean stand biomass; (**): percentage difference between the cross-validation RMSE of the hybrid model compared with the same statistic obtained by cross-validation of the linear model fitted to the complete database.
| Group | Parameter | Estimate | Standard error |
Cross-validation | RMSE reduction** (%) |
|
|---|---|---|---|---|---|---|
| RMSE (Mg ha-1) |
R 2 | |||||
| A | Abs. Shortw. solar rad. | 0.1004 | 0.0523 | 19.85 (38.57%)* |
0.2605 | 14.73% |
| Entropy 3×3 | -143.8093 | 32.8994 | ||||
| Correlation 3×3 | -35.0613 | 11.0553 | ||||
| Dissimilarity 5×5 | 12.3776 | 2.9020 | ||||
| Mean 7×7 | 1.6886 | 0.4856 | ||||
| B | Band 1 | 4.5965 | 0.7375 | 16.87 (21.42%)* |
0.2591 | 18.97% |
| Band 5 | -2.1912 | 0.5013 | ||||
| C | Intercept | 360.9605 | 102.8189 | 26.71 (25.76%)* |
0.1382 | 1.05% |
| Band 1 | -4.7552 | 1.9528 | ||||
| Correlation 3×3 | -137.3135 | 41.1643 | ||||
| D | Flow solar rad. | -0.2223 | 0.0667 | 31.38 (20.38%)* |
0.6149 | 46.14% |
| NDVI | 745.2892 | 112.9641 | ||||
| Stand. Dev. 7×7 | -7.0717 | 2.0254 | ||||
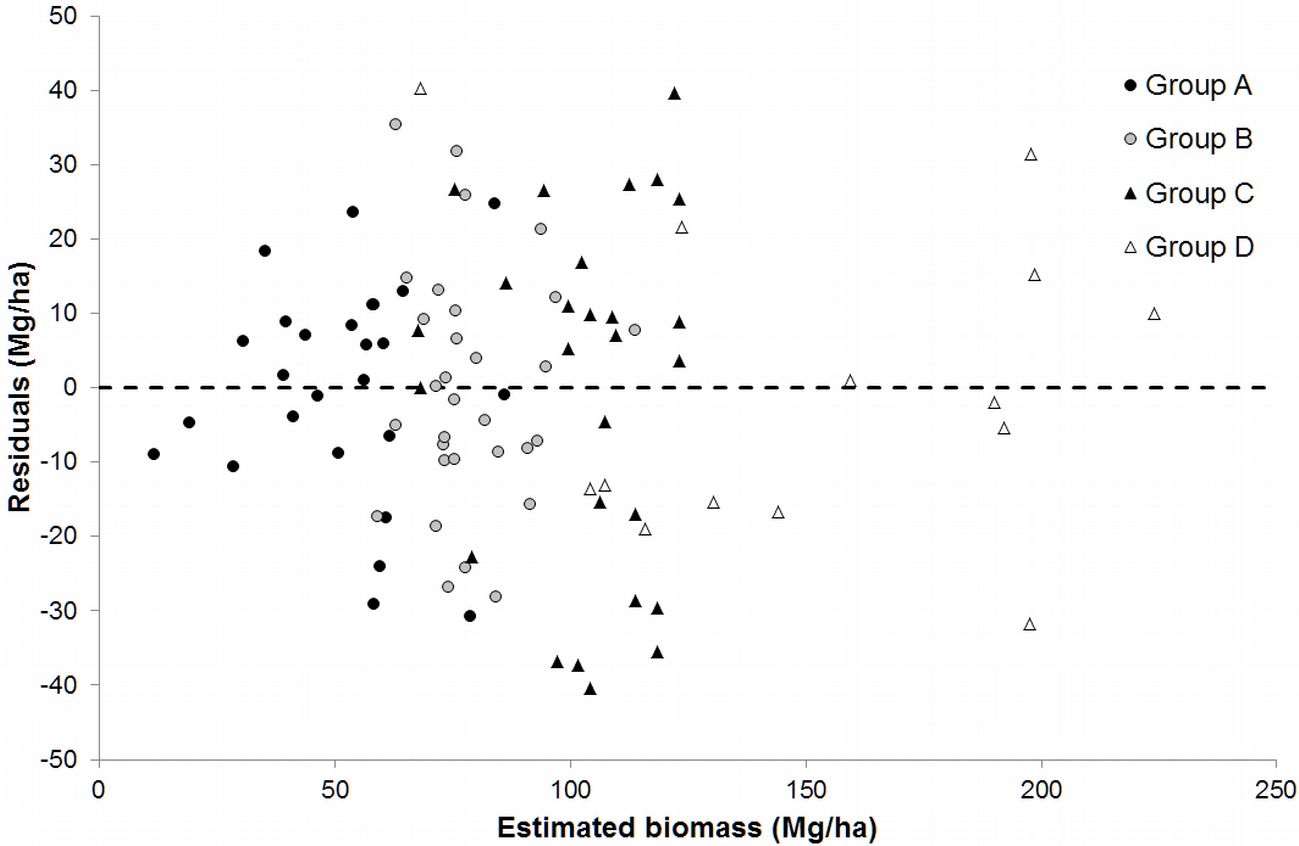
The intercepts of models for groups A, B and D were not significant at the 5% level, and therefore the models were refitted without this term. In all cases, the parameters were significant and the condition number values indicate no problems associated with multicollinearity. Analysis of the graph of the residuals plotted against the predicted values also indicated the absence of problems associated with variance heterogeneity or lack of normal distribution of the residuals (Fig. 4).
Fig. 4 - Plot of residual values against estimated biomass for groups obtained from the classification tree.
Cross-validation of the hybrid model comprising the pruned regression tree (Fig. 3) and the linear models for each terminal node explained 72.96% of the observed variation in stand biomass, with a RMSE value of 22.59 Mg ha-1 (25.37% of the mean stand biomass).
The spatial distribution of the biomass estimation (Mg ha-1) in the study area obtained by application of the classification rules included in the regression tree model and the posterior estimations yielded by multiple linear regression are shown in Fig. 5. The grey and green pixels reflect biomass contents lower than 80 Mg ha-1 and between 80 and 157 Mg ha-1, respectively, whereas the yellow and red pixels represent the highest biomass values found in temperate forest (mainly pine and pine-oak cover) in the study area, in accordance with the INEGI’s Land Use and Vegetation chart, series V (INEGI 2012).
Discussion
The results of the present research showed that integration of spectral information, texture variables derived from the NDVI and terrain indexes (DEM) was essential for forest biomass estimation. Indeed, these variables were reported in previous studies as being closely related to the development and growth of this type of ecosystem and are also useful for ecosystem evaluation and monitoring ([47], [12], [15]).
The combined use of regression trees and linear models including spectral, texture and terrain variables proved to be a good method for identifying patterns and defining biomass trends in the study area. The independent variable albedo, defined as the average solar reflectance ([43]), was the main discriminating factor in the regression tree, and highest values occurred in the areas with the lowest forest biomass. Kuusinen et al. ([41]) obtained similar results and observed an inverse relationship between stand age and albedo, so that the value of this variable was lower in mature stands because of the lower level of incident radiation absorbed in such stands. This relationship can be used to discriminate zones with different levels of forest biomass. The other two discriminant variables were spectral band 7 (short-wave infrared) and the topographical wetness index. Because of its spectral characteristics, band 7 is directly related to the moisture content of soil and vegetation recorded by the image. Thus, the reflectivity in this band increased as the surface wetness captured by the sensor decreased. In afforested areas, this band displays low reflectivity; as moisture levels are high in forest stands, the highest values for this band represent lower amounts of biomass in the classification tree. These results are similar to those reported by García et al. ([22]) for pure stands of Pinus halepensis and P. sylvestris in Spain, i.e., there was an inverse relationship between the values for band 7 of the Landsat-5 TM sensor and the moisture content of the residual forest biomass. Finally, inclusion of the topographic wetness index in the model confirms the previous findings, as high values of this index are associated with high levels of moisture, which coincide with zones with high amounts of biomass. In various studies, use of the relationship between the wetness index and the vegetation biomass has enabled identification of the distribution of vegetation ([51], [77]) and of potential areas for establishing forest plantations ([29]). These results indicate water availability as a key factor controlling biomass production in arid and semi-arid environments such as the Sierra Madre Occidental ([65], [48], [75], [19]).
The hybrid model combining the nonparametric method of regression trees and multiple linear models yielded a reduction in the RMSE (25.47%) and an increase in R2 (42.14%) with respect to the same statistics obtained by cross-validation of the linear model fitted to the complete database. According to the results shown in Tab. 5, the main RMSE reduction was obtained in group D (46.14%), probably because this group is associated with sample plots with higher stand biomass values. On the other hand, the reduction in RMSE in group C was only 1.05%, possibly because this is the group with the lowest coefficient of variation of stand biomass (27.23% compared with a mean value of 48.56%).
The parameters selected by the hybrid model included single band values in the visible (Band 1-blue) and mid infrared (Band 5) regions of the electromagnetic spectrum. The mid infrared regions have already been included and discussed in the initial (Band 5 and Band 7) and pruned (Band 7) regression tree model, indicating a relationship between the biomass and spectral response of forest cover in the imagery bands related to water content. As expected, vegetation indexes, such as NDVI, and other indicators of the radiation-land cover interaction, such as the Absorbed Shortwave Solar Radiation, also emerged as valuable predictors of biomass due to their potential relationship with biomass. The relationship between remote sensed NDVI and biomass content, which has been the matter of discussion as strongly dependent on the scale of analyses and characteristics of the imagery, has nonetheless been regarded in the literature as one of the most widely used predictors of biomass content ([18], [26]).
Interestingly, apart from these variables in the pure spectral domain, up to five variables of the spectral-spatial domain (i.e., texture variables Entropy 3×3, Correlation 3×3, Dissimilarity 5×5, Mean 7×7, Stand. Dev. 7×7) were included in the mixed model. This indicates the importance of the spatial arrangement of spectral values at different spatial scales (from a 3×3 kernel corresponding with an area of 0.81 ha to a 7×7 kernel corresponding with an area of 4.41 ha) for forest stand characterization, as reported in previous studies ([20], [36], [15], [56]).
The value of R2 finally obtained with the hybrid model (0.7296) is slightly higher than that obtained by Sun et al. ([69]) in a study carried out in the US, with high resolution LIDAR sensors and SAR data, to model field-measured biomass by linear models and stepwise selection of variables (R2, 0.71 and RMSE, 31.33 Mg ha-1).
Estimates obtained with sensors of medium spatial resolution usually display a low predictive power for each band of the sensor. Thus, Foody et al. ([18]) found the strongest predictive relationship for biomass with a sampling network specifically designed for different sites (r > 0.71) based on indexes obtained for tropical forest in Brazil by using Landsat TM data. On the other hand, Houghton et al. ([30]) estimated the biomass of Russian forests by using data derived from a MODIS sensor and regression trees in 500×500 m plots, in which the percentage of variance explained by regression trees ranged from 1 to 67%.
In the present study, the consideration of biophysical variables derived from satellite images along with other complementary data and the use of nonparametric multivariate techniques, improved the quality of the estimates, thus indicating that this is a promising line of research.
Conclusions
This study explored possible improvements in forest biomass prediction involving use of field data and geodata derived from atmospherically and topographically corrected satellite images (provided by the Landsat-5 TM sensor), texture indexes and DEM-derived terrain variables. A new approach combining the nonparametric regression trees method and multiple regression analysis of the groups defined in the pruned tree was compared with the usual method of fitting a linear model to the complete database. Cross-validation of both methods indicated that the proposed new approach improved the performance of the linear model. Moisture content was an important covariate in the final model and was directly related to biomass distribution in the temperate forest under study. The proposed approach deserves further attention in future studies aimed at estimating stand variables by using remote sensing data, especially for more complicated stand structures, such as mixed and uneven aged forests, in which the use of a mean value for each node cannot accurately represent the intra-node stand variation.
Acknowledgements
This research was supported by SEP-PROMEP (Project: Seguimiento y Evaluación de Sitios Permanentes de Investigación Forestal y el Impacto Socioeconómico del Manejo Forestal en el Norte de México). We thank three anonymous reviewers for their useful comments and suggestions, which helped to improve an earlier version of the manuscript.
References
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
DICAF, Universidad Juárez del Estado de Durango, Boulevard del Guadiana 501, Ciudad Universitaria, Torre de Investigación, 34120 Durango, Dgo (México)
José J Corral-Rivas
Instituto de Silvicultura e Industria de la Madera, Universidad Juárez del Estado de Durango, Boulevard del Guadiana 501, Ciudad Universitaria, Torre de Investigación, 34120 Durango, Dgo (México)
Departamento de Botánica - IBADER, Universidad de Santiago de Compostela, Escuela Politécnica Superior, Lugo (España)
Facultad de Ciencias Forestales, Universidad Juárez del Estado de Durango, Río Papaloapan 132, Valle del Sur Durango, 34120 Durango, Dgo (México)
División de Estudios de Posgrado e Investigación, Instituto Tecnológico de El Salto, Mesa del Tecnológico s/n, 34942, El Salto, Dgo (México)
Departamento de Ingeniería Agroforestal, Universidad de Santiago de Compostela, Escuela Politécnica Superior, Lugo (España)
Corresponding author
Paper Info
Citation
López-Serrano PM, López-Sánchez CA, Díaz-Varela RA, Corral-Rivas JJ, Solís-Moreno R, Vargas-Larreta B, Álvarez-González JG (2015). Estimating biomass of mixed and uneven-aged forests using spectral data and a hybrid model combining regression trees and linear models. iForest 9: 226-234. - doi: 10.3832/ifor1504-008
Academic Editor
Davide Travaglini
Paper history
Received: Nov 17, 2014
Accepted: May 17, 2015
First online: Sep 21, 2015
Publication Date: Apr 26, 2016
Publication Time: 4.23 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 55376
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 44857
Abstract Page Views: 3763
PDF Downloads: 5119
Citation/Reference Downloads: 73
XML Downloads: 1564
Web Metrics
Days since publication: 3773
Overall contacts: 55376
Avg. contacts per week: 102.74
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2016): 13
Average cites per year: 1.30
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Review Papers
Remote sensing-supported vegetation parameters for regional climate models: a brief review
vol. 3, pp. 98-101 (online: 15 July 2010)
Review Papers
Accuracy of determining specific parameters of the urban forest using remote sensing
vol. 12, pp. 498-510 (online: 02 December 2019)
Review Papers
Remote sensing of selective logging in tropical forests: current state and future directions
vol. 13, pp. 286-300 (online: 10 July 2020)
Technical Reports
Detecting tree water deficit by very low altitude remote sensing
vol. 10, pp. 215-219 (online: 11 February 2017)
Research Articles
Modelling dasometric attributes of mixed and uneven-aged forests using Landsat-8 OLI spectral data in the Sierra Madre Occidental, Mexico
vol. 10, pp. 288-295 (online: 11 February 2017)
Research Articles
Assessing water quality by remote sensing in small lakes: the case study of Monticchio lakes in southern Italy
vol. 2, pp. 154-161 (online: 30 July 2009)
Research Articles
Classification of xeric scrub forest species using machine learning and optical and LiDAR drone data capture
vol. 18, pp. 357-365 (online: 07 December 2025)
Research Articles
Afforestation monitoring through automatic analysis of 36-years Landsat Best Available Composites
vol. 15, pp. 220-228 (online: 12 July 2022)
Technical Reports
Remote sensing of american maple in alluvial forests: a case study in an island complex of the Loire valley (France)
vol. 13, pp. 409-416 (online: 16 September 2020)
Review Papers
Remote sensing support for post fire forest management
vol. 1, pp. 6-12 (online: 28 February 2008)
iForest Database Search
Google Scholar Search
Citing Articles
Search By Author
- PM López-Serrano
- CA López-Sánchez
- RA Díaz-Varela
- JJ Corral-Rivas
- R Solís-Moreno
- B Vargas-Larreta
- JG Álvarez-González
Search By Keywords