Shear modulus of old timber
iForest - Biogeosciences and Forestry, Volume 10, Issue 2, Pages 446-450 (2017)
doi: https://doi.org/10.3832/ifor1787-009
Published: Mar 24, 2017 - Copyright © 2017 SISEF
Research Articles
Abstract
Interest in both the time effect on the timber mechanical properties and the reuse of old solid timbers has prompted many research works since the 1970s, mainly focusing on evaluating bending strength (MOR) and stiffness (MOE). However, only few studies have investigated the effect of aging on shear modulus (G). In this work, transverse vibration test is used to calculate G and MOE of over 80 old timber beams. The MOE/G ratio and the relationship between G and different timber features are investigated. The main outcome of the research confirms that the MOE/G ratio is around 20, close to the value reported in literature for new solid timber. No relationship exists between G and MOE (r2=0.07) or between G and other timber features. When density and knots are used as predictors in a multiple regression model, the G prediction improves (r2=0.22). This work confirms that G is not affected by the age of timber.
Keywords
Flexural Vibration, Old Timber, Historical Timber Buildings, Reclaimed Timber
Introduction
The interest in recycling old timber has increased recently ([16]). Salvaged timbers can be reused for making furniture, interior design and restoration works. Brandon Davis ([5]) presented a detailed and thorough review of benefits and opportunities of using reclaimed wood. To reuse reclaimed timber in wood construction, the mechanical properties must be taken into consideration. Many research works have investigated the aging effects on the bending Modulus of Elasticity (MOE) or the bending strength (MOR) of old timber, since the MOE is well related to the overall quality of timber and MOR is usually the most important and limiting factor in timber structures. In some cases, the mechanical properties of wood were not being significantly affected by aging process if the wood is preserved by decay phenomena ([18], [10], [27], [29], [34], [16]). Other works reported a significant bending strength reduction ([1], [23], [20]). This explains why the effect of aging on the mechanical properties of old timber is still of interest for architects and structural engineers.
Shear modulus (G) is the ratio of shear stress to shear strain, describing the material’s response to shear stress. It is a basic property of materials, essential for the efficiency of construction procedures ([35]) when short members are considered within a structure or for parts subjected to torsion action and when timber is loaded in bending, because in nearly all cases, deflection is also affected by G. It is also used by structural engineers for finite element analysis and for various strengthening intervention designs such as beams ends prosthesis. Finally, the MOE/G ratio is used in design equations to determine torsional rigidity and to predict structural beams’ lateral torsional stability.
Shear modulus is usually assumed as a portion of MOE, because in clear wood both are related to the density and the microfibril angle within the cell walls. For structural timber, G is also affected by many other features such as slope of grain, knots and presence of pith.
The determination of G by mechanical tests is quite difficult, it is biased by errors and it is time-consuming ([4]), so many researchers used dynamic methods applied to small specimens. Chui ([7]) calculated the G values comparing clear and unclear small specimens obtained from the same boards to evaluate the effect of knots on both MOE and G. Divos et al. ([9]) investigated the relationship between statically and dynamically determined G on small specimens. Carreira ([6]) used transverse vibration test to calculate the MOE/G ratio of 20 full dimension logs (2.25 m long, 16 cm diameter). Kránitz et al. ([16]) and Noguchi et al. ([21]) investigated the G value of small clear specimens obtained from old timber beams, demonstrating that G is not affected by age. Recently, Olsson & Källsner ([22]) used the transverse vibration test to evaluate both MOE and G and their relationship on Norway spruce boards, reporting that G largely depends on density and is poorly correlated to the MOE. The goals of this research are to calculate the shear modulus of structural timber coming from different historical buildings, to investigate the relationship between G, timber features (density, knots, slope of grain, ring shake) and MOE, and to compare them to the values reported in the literature for new structural timber.
Materials and methods
Materials
Eighty-four structural timber beams were tested and carefully inspected. Seventeen were spruce (Picea abies Karst.), and 67 were silver fir (Abies alba Mill.). Since the two species have similar physical and mechanical properties, they were considered together in this work, as many visual grading rules state for new timber. Based on the historical research, all the beams are older than 70 years, so it is possible to suppose that they were not subjected to high stress levels during their service life, according to the effect of the duration of load ([14]). In the original buildings, the beams were mainly used as part of trusses (rafters and tie beams) and floor beams, and consequently were subjected to different stress actions (bending, compression and tension).
The average cross-section of the beams was between 14×14 and 28×22 cm2, and the average length was about 470 cm.
Different timber features affecting the mechanical properties of wood were observed and recorded.
- Slope of grain: calculated as the angle between the fibre orientation and the longitudinal axis of the timber. It is an important factor affecting the elastic properties of wood.
- Knots: they affect both MOE and G. In this work, knots were evaluated according to the visual strength grading rules of solid timber UNI-11119 ([30]) and UNI-11035-1/2 ([31]), as the ratio between the minimum diameter of a knot and the dimension of the face on which it appears, and recording the maximum observed value.
- Wane: their dimensions were measured, and the ratio between the cathetus and the length of its corresponding face was calculated. Wane are quite common in old structural timber of large dimension, though it is well known that they do not reduce the mechanical properties of timber ([28]).
- Ring shake: it is a discontinuity between two consecutive annual rings that reduces the cross-section and affects shear strength and modulus. In this work, it was calculated according to UNI-11035-1/2 ([31]), by measuring the distance between the pith and the ring shake.
- Decay and insect damages: presence and extension of decay and insects attacks were observed and recorded to identify the real cross-section of each timber.
- Other damages: since it is quite common to observe damages (like holes) in old timber caused by mounting and dismounting operations, all of them were recorded.
- Checks: since the pith was always included in the tested beams, checks appear as a consequence of the drying process. Their extensions in the longitudinal and transverse directions were measured.
- Density: directly related to mechanical properties and used for G calculation. All the beams were measured and weighed to calculate density as the mass to volume ratio (volume calculated by multiplying the length for the average cross-section measured at the ends and at 1/3 and 2/3 of the length).
- Moisture content (MC): it was calculated using gravimetric method on clear specimens after testing timber at failure. Tab. 1 reports the MC range and variation. In softwood species, MOE and G vary linearly by about 1.5% and 2.2%, respectively, every 1% MC below the fibre saturation point ([32]). Therefore, no correction was applied to MOE or G. The quality of the tested beams was strongly variable, as when they were used, no standardized selection was made based on quality. Thus, the sample contains beams of good quality (high density, small knots, no slope of grain) as well as beams of poor quality (large knots and high slope of grain, mainly) that are not suitable for structural uses based on modern grading rules.
Tab. 1 - Descriptive statistics for density (ρ), Modulus of Elasticity (MOE), shear modulus (G) and MOE/G ratio of the tested timber beams. (MC): moisture content.
| Parameter | ρ (kg m-3) |
MC (%) |
MOE (MPa) |
G (MPa) |
MOE/G |
|---|---|---|---|---|---|
| min | 335 | 10 | 2795 | 201 | 7 |
| max | 570 | 19 | 15575 | 613 | 36 |
| average | 422 | 13 | 8626 | 398 | 21 |
| CV (%) | 11 | 6.6 | 30 | 28 | 33 |
The timber beams showed different conservation status. Only 24 were affected by decay, for all of them the position and extension of decay were recorded. According to Gilfillan & Gilbert ([11]) and Cruz & Machado ([8]), the effect of insect attack was negligible. In this work, none of the tested beams was affected by severe attacks, and the attacks were limited to the sapwood, as determined by visual inspection. Therefore, both research works demonstrated that for the investigated species strength does not decrease considerably, even when the level of the attack is high.
Only 12 timbers presented ring shakes of various extensions. Ring shake and checks affect not only mechanical properties, but also the mode of vibration in dynamic tests. When the extension of such defects is too large, the timber beams response in flexural vibration is biased, the frequencies of vibration change, the results do not converge and those beams were excluded from the analysis (see below).
Dynamic tests
Dynamic methods have been used in several studies to evaluate G and for the simultaneous evaluation of G and MOE ([7], [9], [19], [15], [6], [16], [22]). Those methods combine the reliability of the results with the simplicity and rapidity required to carry out the tests. Vibration test is a simple and efficient way to characterise the elastic properties of timber; in fact, it has been used since the ’80s for assessing timber quality.
Transverse vibration tests are based on the resolution of the motion equations of flexural vibrations. Different authors have proposed various theoretical models and solutions characterised by specific validity ranges and accuracy levels ([3]). In 1921, Timoshenko proposed the differential equation for motion. Different solutions were lately proposed by Goens ([12]), Rayleigh ([24]) and Bordonné ([2]).
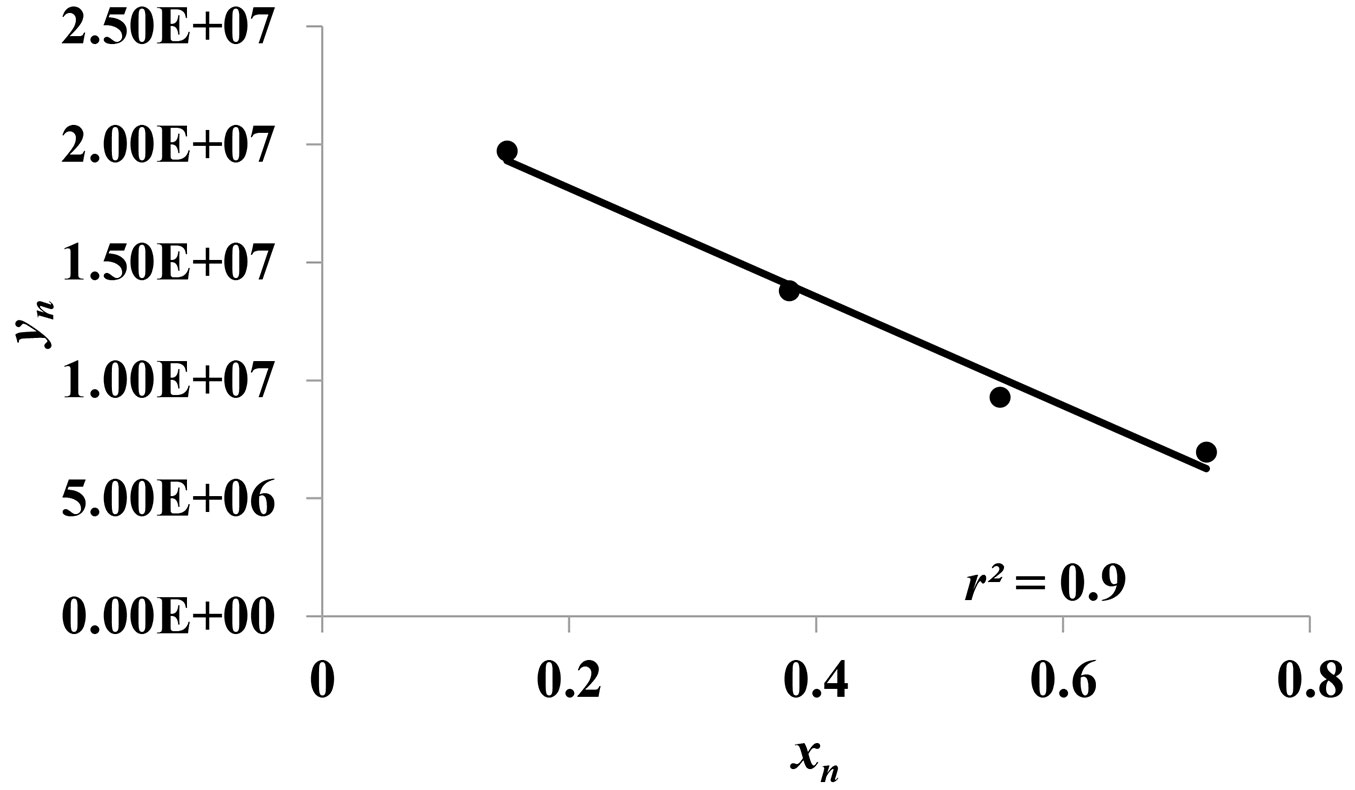
Frequency equations allow calculation of both G and MOE. Chui ([7]) proposed a method for the calculation of MOE and G based on the first two vibration frequencies. An alternative method to calculate G based on the same vibration test was proposed by Kubojima et al. ([17]). In this work, the Bordonne’s solution to Timoshenko’s model was adopted for the simultaneous calculation of G and MOE. The same method has already been used by other authors to calculate G and MOE ([26], [25], [33]). This solution can be applied only when the length to depth ratio of the beam is higher than 10 (the minimum ratio of the tested beam is 15), which is applicable in this case. This solution considers the first 3 to 5 vibration frequencies of each beam. For each beam, the equation system is solved, and a pair of coordinates (xn, yn) are computed. The coordinates are reported in a Cartesian coordinate system and fitted with a trend line (Fig. 1), where the intercept represents the specific MOE (MOE/ρ) and the slope corresponds to the MOE to G ratio. In our case, four frequencies were considered and four couple of coordinates computed using the following equation (eqn. 1):
where ρ is the density, k is the Timoshenko’s shear correction factor (0.83 for rectangular and squared section), G the shear modulus in vibration plane and MOE the dynamic Modulus of Elasticity.
Only the regression curves with a coefficient of determination (r2) higher than 0.9 were used, as lower r2 indicates biased mode of vibration; therefore, only 81 beams were considered in the study. The excluded beams presented too much extended and deep checks or ring shakes or higher deformation.
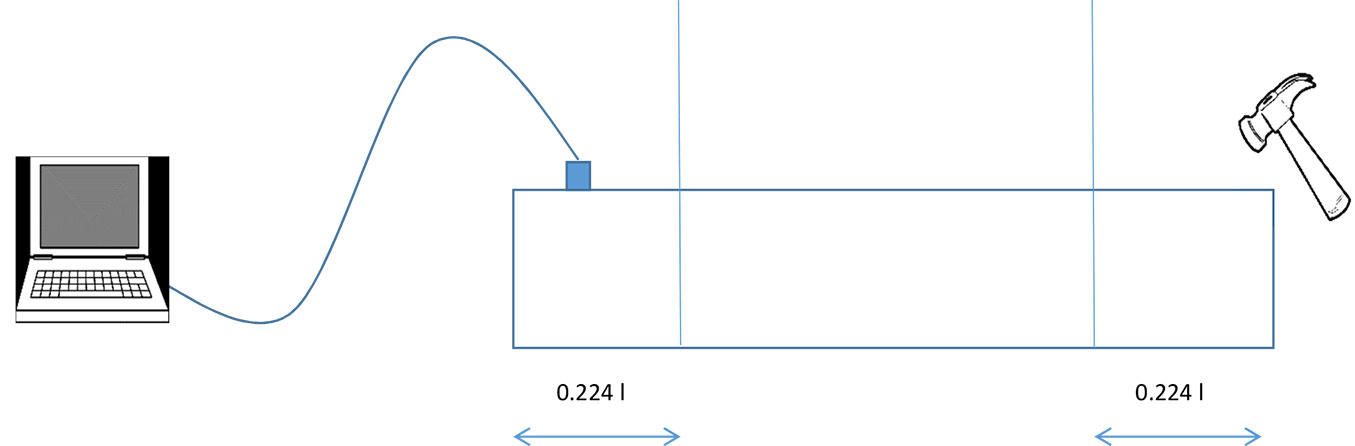
All the beams were suspended by two threads at their theoretical nodes (points of zero vibration) and tested in free-free flexural vibration (Fig. 2). Transverse vibration was induced by striking the beams using a hammer in the direction of the depth. A piezoelectric accelerometer (PCB 480E09®, PCB Piezotronics Inc., Depew, NY, USA) was placed on the opposite part of the beam to acquire the mode of vibration. The signal was processed by Fast Fourier Transform (FFT), and the resonant frequencies were identified using a LabVIEW® software application (National Instruments Corp., Austin, TX, USA). In this paper, only the results concerning G and MOE/G calculated using a dynamic technique are reported and discussed.
Results and discussion
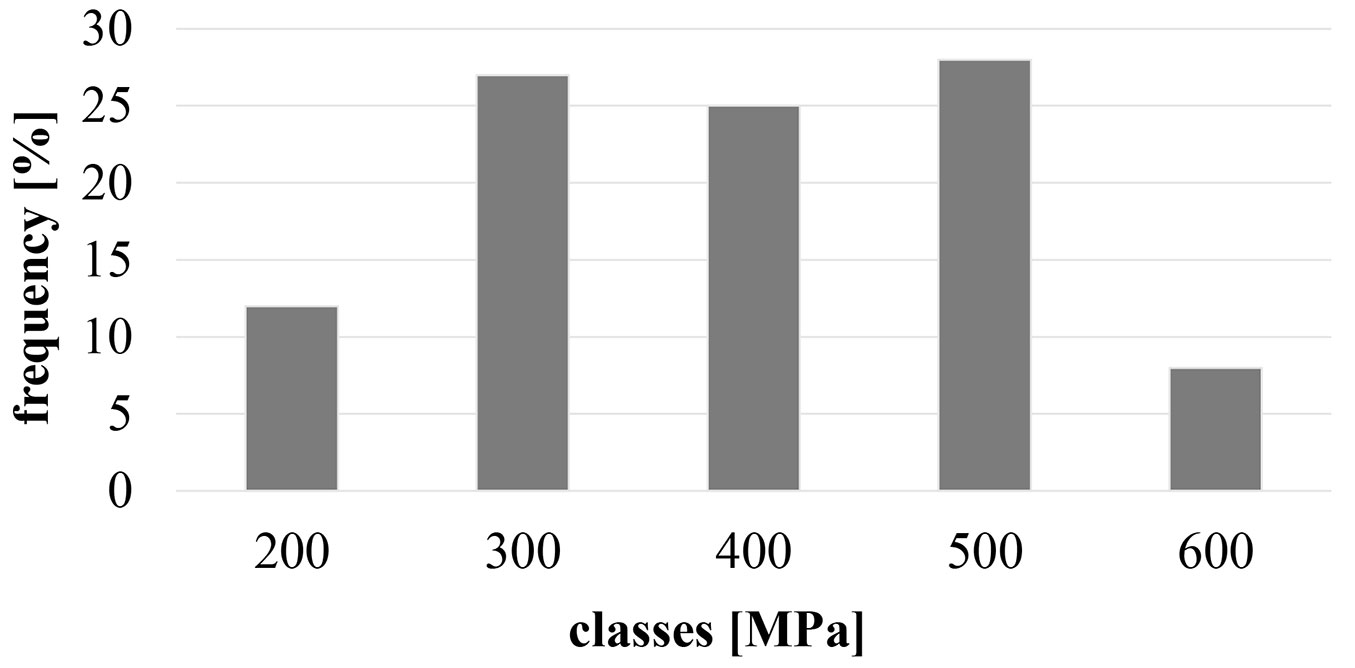
Tab. 1 shows the average values of the main physical and mechanical properties. The average G was approximately 400 MPa; it has to be stressed that more than 50% of the beams had G value higher than 350 MPa (Fig. 3). Variability was quite high (CV=28%) as a consequence of the high variability of the material itself. CV was around 30% for both G and MOE. The mean MOE/G for the tested material was 21 (minimum 7, maximum 36).
Due to the characteristics of the tested materials (structural timber of various quality and state of conservation), it is quite difficult to compare G to the results reported in literature because it is usually obtained with very different conditions (new material, small clear specimens, small unclear specimens, static tests, dynamic tests, etc.). In this case, it is much more suitable to compare the MOE/G ratio obtained in different research works based on the application of dynamic tests (Tab. 2).
Tab. 2 - Summary of previous experimentally obtained MOE/G values. (*): free-free flexural vibration test; (**): ultrasound velocity test.
| Authors | MOE/G | Type | Specimen dimensions |
Species |
|---|---|---|---|---|
| Chui ([7])* | 23 | small clear/unclear (new wood) | 40 × 40 × 640 mm3 | White spruce |
| Noguchi et al. ([21])* | 8 | small clear specimens (aged wood) | ≈2.2 × 14 × 110 mm3 | Pinus densiflora |
| Carreira ([6])* | 19 | logs (new wood) | 0.16 m ø × 2.25 m | Eucalyptus citriodora |
| Kránitz et al. ([16])** | 27 | small clear specimens (aged wood) | 25-95 × 95-497 × 1230-2645 mm3 | Norway spruce |
| Olsson & Källsner ([22])* | 15-17 | lumbers (new wood) | 44 × 145 × 3600 mm3 | Norway spruce |
Kránitz et al. ([16]) and Noguchi et al. ([21]) stated that aging has no significant effects on MOE/G. Both works tested small clear specimens of old wood oriented along a longitudinal-radial direction ([21]) and in longitudinal-radial/longitudinal-tangential direction ([16]). The authors reported significantly different MOE/G (27 and 8, respectively). This difference is a consequence of the different dimensions and orientations of the tested specimens and also of the different dynamic techniques used. These values are also different from the MOE/G calculated within this study for several reasons. In structural timber, defects affect both G and MOE, and structural timbers are usually not oriented along the main anatomical directions, but rather a mix of longitudinal-radial and longitudinal-tangential directions, which justifies the larger variability of the results.
Studies focused on materials with defects report a MOE/G ratio closer to the outcomes reported in this investigation. Chui ([7]), tested a mixed sample of clear and unclear small specimens, reporting a MOE/ G = 23. Carreira ([6]) tested logs of dimension closer to the materials used in this research and reports an average MOE/G = 19. The MOE/G obtained here shows higher variability compared to the Carreira’s results as a consequence of the characteristics of the material itself. This author tested highly homogeneous material (CV lower than 10% for all mechanical properties) by exciting it in the same anatomical direction. Olsson & Källsner ([22]) reported a MOE/G in the range of 15-17 for Norway spruce lumbers.
These results confirm that MOE and G are affected by defects in different ways, as previously reported by Chui ([7]) and Gupta et al. ([13]). The effect of knots on G is related to their number, position and orientation, as reported by Gupta et al. ([13]) and Olsson & Källsner ([22]). The importance of knots seems to be confirmed in this study, since the relationship between knots and G showed the higher correlation value between G and all the timber features (r2 = 0.11, p < 0.01), and the knots were evaluated according to two visual grading rules ([30], [31]) that considered only the largest one in a beam, without taking into account their number, position and orientation. Knots and MOE did not show any significant correlation (r2 = 0.003, p>0.05), confirming that the MOE is not influenced by local defects. Thus, knots seem to have a greater effect on G than on MOE, suggesting that using G to improve the bending strength prediction could be valid also for old timber, as proposed by Olsson & Källsner ([22]).
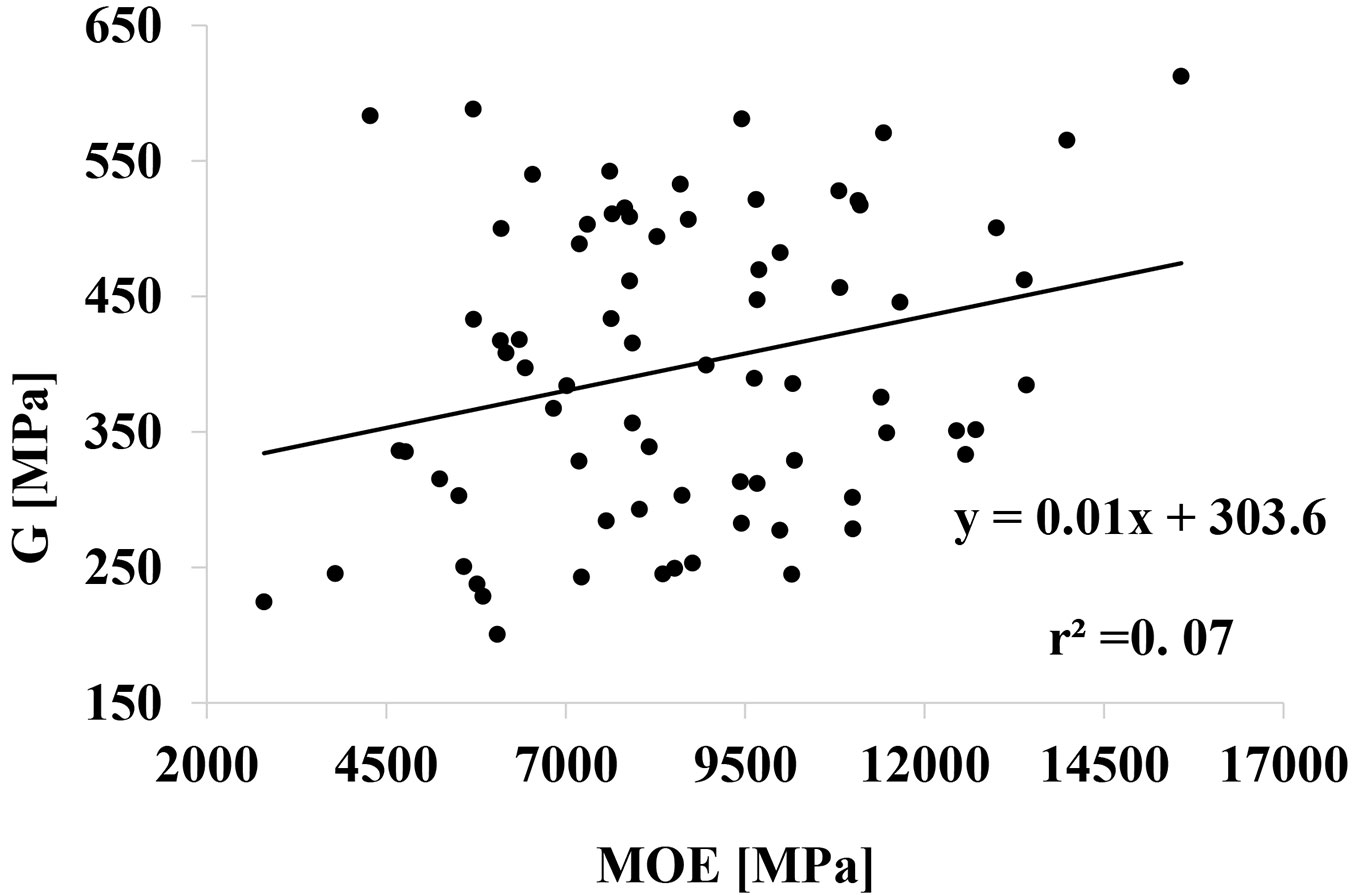
No relationship was found between G and other timber features such as density, slope of the grain, presence and extension of ring shakes and wane. Additionally, MOE and G did not show significant relationships (r2 = 0.07, p>0.05 - Fig. 4), as already reported in the literature ([7], [22]).
Fig. 4 - Relationship between modulus of elasticity (MOE) and shear modulus (G). 0.07 > p-value > 0.01.
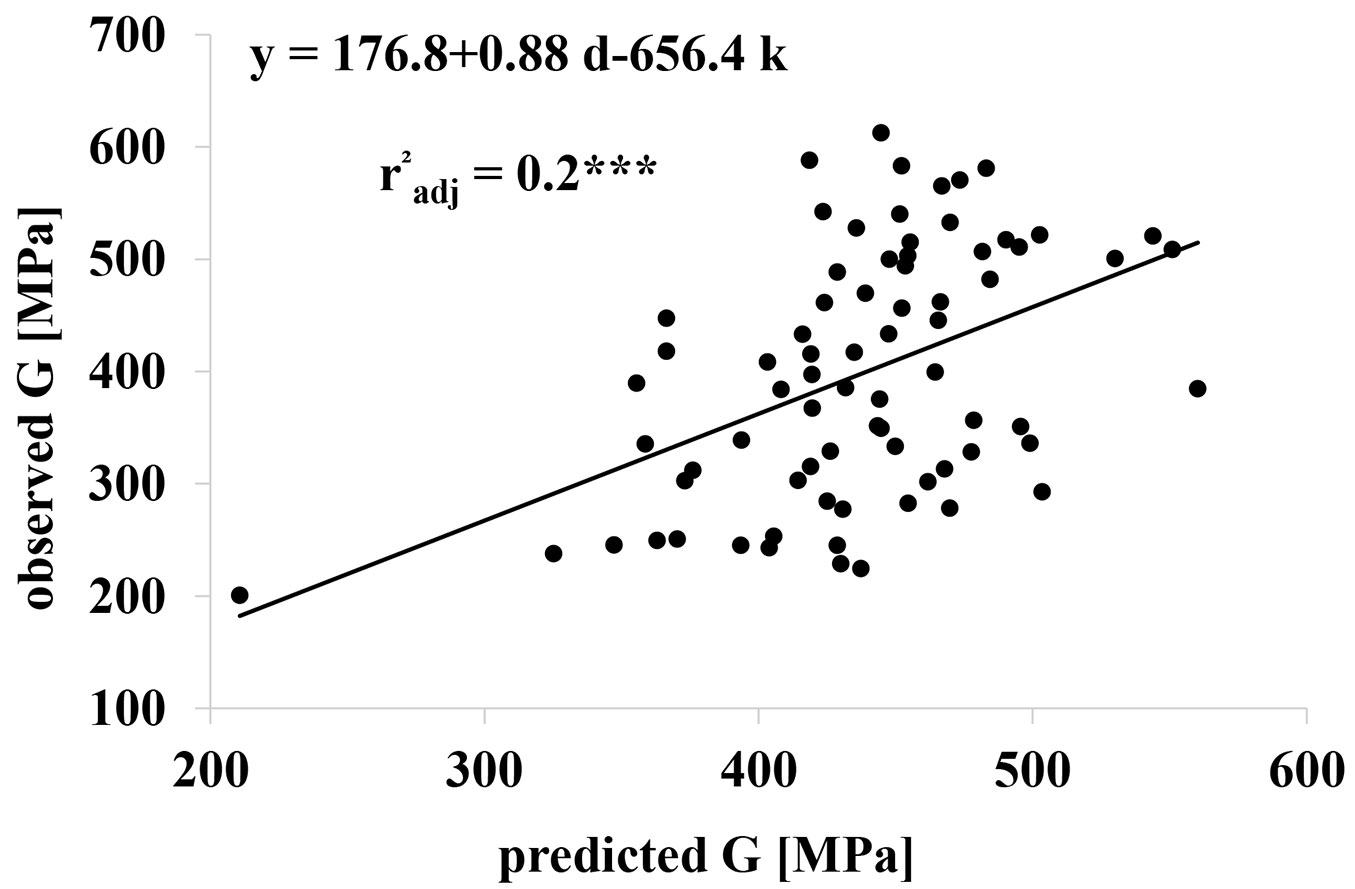
An improvement in the G prediction is possible using knots and density as predictors in a multiple linear regression (r2= 0.2, p<0.01 - Fig. 5). This is because, according to many authors ([7], [13], [22]), the driving factors for G are density and knots. The multiple regression analysis confirmed the results reported by Olsson & Källsner ([22]), who used MOE and density as regressors to predict G (r2= 0.39). Indeed, they found that MOE was correlated to the presence of important defects like the quantity of knots and the slope of grain that have important effects in increasing G. The lower accuracy in predicting G obtained in this study is likely due to the larger variability of the old timber analyzed, as compared with the new materials tested by Olsson & Källsner ([22]).
Fig. 5 - Shear modulus (G) prediction using knots (k) and density (d) (knots considered according to the standard - [31]). p-value < 0.01.
Conclusions
Eighty-four old timber beams were dynamically tested by means of free-free flexural vibration test. Applying the Bordonné solution, both G and MOE were calculated simultaneously.
The mean G for the whole sample was of about 400 MPa, and the average MOE/G was around 21, close to the value reported in different papers for unclear specimens and for new structural timber.
No relationships were found between G and MOE (r2 = 0.07) or between G and other timber features (slope of grain, density, etc.). The relationship between G and knots, though limited (r2 = 0.11), seems to confirm the results previously reported in the literature. This suggests an important effect of knots, their dimensions and orientations on the G values that requires further in-depth investigation. These results are consistent with those reported in the literature both for new structural timbers and unclear specimens, confirming also that G, like other mechanical properties of wood, is not significantly affected by aging.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Online | Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Daniele Cibecchini
Giacomo Goli
Marco Togni
GESAAF - Department of Agricultural, Food and Forestry Systems - Section Forestry, Environment, Wood, Landscape, University of Florence, v. San Bonaventura 13, I-50145 Florence (Italy)
Corresponding author
Paper Info
Citation
Cavalli A, Cibecchini D, Goli G, Togni M (2017). Shear modulus of old timber. iForest 10: 446-450. - doi: 10.3832/ifor1787-009
Academic Editor
Andrea Cutini
Paper history
Received: Jul 31, 2015
Accepted: Nov 12, 2016
First online: Mar 24, 2017
Publication Date: Apr 30, 2017
Publication Time: 4.40 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2017
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 49130
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 41236
Abstract Page Views: 2706
PDF Downloads: 3925
Citation/Reference Downloads: 34
XML Downloads: 1229
Web Metrics
Days since publication: 3143
Overall contacts: 49130
Avg. contacts per week: 109.42
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
(No citations were found up to date. Please come back later)
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Comparison of timber-house technologies and initiatives supporting use of timber in Slovenia and in Sweden - the state of the art
vol. 10, pp. 930-938 (online: 07 December 2017)
Research Articles
Modifying harvesting time as a tool to reduce nutrient export by timber extraction: a case study in planted teak (Tectona grandis L.f.) forests in Costa Rica
vol. 9, pp. 729-735 (online: 03 June 2016)
Research Articles
Analysis and evaluation of the impact of stand age on the occurrence and metamorphosis of red heartwood
vol. 10, pp. 605-610 (online: 15 May 2017)
Research Articles
Deploying an early-stage Cyber-Physical System for the implementation of Forestry 4.0 in a New Zealand timber harvesting context
vol. 17, pp. 353-359 (online: 13 November 2024)
Research Articles
Assessment of timber extraction distance and skid road network in steep karst terrain
vol. 10, pp. 886-894 (online: 06 November 2017)
Research Articles
Fuel consumption comparison of two forwarders in lowland forests of pedunculate oak
vol. 12, pp. 125-131 (online: 11 February 2019)
Research Articles
The effect of provenance of historical timber on tree-ring based temperature reconstructions in the Western Central Alps
vol. 13, pp. 351-359 (online: 25 August 2020)
Research Articles
Energy and environmental profile comparison of TMT production from two different companies - a Spanish/Portuguese case study
vol. 11, pp. 155-161 (online: 07 February 2018)
Technical Advances
Technical properties of beech wood from aged coppices in central Italy
vol. 8, pp. 82-88 (online: 04 June 2014)
Research Articles
Identification of wood from the Amazon by characteristics of Haralick and Neural Network: image segmentation and polishing of the surface
vol. 15, pp. 234-239 (online: 14 July 2022)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword