Using self-organizing maps in the visualization and analysis of forest inventory
iForest - Biogeosciences and Forestry, Volume 5, Issue 5, Pages 216-223 (2012)
doi: https://doi.org/10.3832/ifor0629-005
Published: Oct 02, 2012 - Copyright © 2012 SISEF
Research Articles
Abstract
A lot of useful data on forest condition can be gathered from the Forest Inventory (FI). Without the help of data analysis tools, human experts cannot manually interpret information in such a large data set. Conventional multivariate statistical analyses provide results that are difficult to interpret and often do not represent the information in a satisfactory way. Our goal is to identify an alternative approach that will enable fast and efficient interpretation and analysis of the FI data. Such interpretation and analysis can be performed automatically with a clustering method, but all clustering methods have some shortcomings. Therefore, our aim was also to provide information in a form suitable for fast and intuitive visualization. Kohonen’s Self Organizing Map (SOM) is an alternative approach to data visualization and analysis of large multidimensional data sets. SOM provides different possibilities and our experiments are presented with component matrices of individual stand parameters and label matrices. In forming data clusters, we experimented with hierarchical and non hierarchical clustering methods. Our experiments showed that SOM provides useful information in a form suitable for data clustering and data visualization. This enables an efficient analysis of large FI data sets at different analysis scales. Clustering results obtained with SOM and two clustering algorithms are in accordance with ground truth. We have also considered the efficiency of SOM component matrices by visual comparison and correlation among structural parameters and by determining contributions of individual stand parameters to clustering input data. SOM application in visualization and analysis of stand structural parameters enables gathering quickly and efficiently holistic information on the current condition of forest stands and forest ecosystem development. Therefore we recommend the application of Kohonen’s SOM for visualization and analysis of FI data.
Keywords
Forest Inventory, Stand Structural Parameters, Self-organizing Maps, Forest Data Visualization, Neural Networks
Introduction
Information on the condition of a forest can be gathered in many ways. Modern forest management mostly uses Forest Inventory (FI), which is a statistical description of the quantitative and qualitative attributes of forest resources in a given region ([5]). FI provides relevant information necessary for everyday forest management decision making. Forest measurement methodologies have been significantly improved both in spatial and in temporal domain, by using georeferenced maps, implementing remote sensing, using the global positioning system, geographical information system (GIS) and artificial intelligence methods ([25], [16]).
Application of artificial Neural Networks (NN) in ecology started in mid 1990s. Somewhere around that time, the first applications of NN in forestry have emerged as an alternative to the conventional multivariate statistical analysis in modeling of nonlinear and complex phenomena in forestry science ([30], [18]). NN have been successfully applied to many forestry problems ([23]). Many different types of NN have been studied and successfully applied in various fields, but NN with supervised learning and error back propagation algorithm have been the most commonly used type of neural networks. The unsupervised learning NN models, such as Adaptive Resonance Theory, Hopfield Neural Network or Kohonen’s Self Organizing Map (SOM) are less popular though successfully applied. Among them, Kohonen’s SOM type neural network has some good and interesting features ([19]). It combines a high degree of biological plausibility with applicability to many information processing and optimization problems ([35]).
Research community has confirmed the usefulness of SOM in different areas of forestry, both as a standalone tool and in combination with other methods. Hasenauer & Merkl ([10]) compare LOGIT model and SOM in predicting tree mortality of Norway spruce (Picea abies L. Karst) in Austria. Giraudel & Lek ([9]) compare SOM algorithm and some conventional statistical methods for ecological community ordination. Sulkava & Hollmén ([36]) outline that the nutrient concentrations of Norway spruce (Picea abies) and Scots pine (Pinus sylvestris) needles in Finland were analyzed by SOM clustering. Fujino & Yoshida ([8]) investigate the development and validation of a method of forestry region classification using PCA and cluster analysis together with SOM. Park & Chung ([29]) apply SOM and Multilayer Perceptron (MLP) to the classification and prediction of the level of pine tree vulnerability to the insect Thecodiplosis japonensis. Foody & Cutler ([6]) use two neural network models (supervised: MLP, RBF, GRNN and SOM) to derive biodiversity information about tropical forests (north eastern Borneo, Malaysia) from the remotely sensed imagery (Landsat TM). Annas et al. ([1]) use PCA and SOM for the analysis of fire risks in forest regions. Lippitt et al. ([22]) investigate the capability of three artificial neural networks: MLP, SOM, and Fuzzy ARTMAP and two decision trees (Entropy and Gini) splitting rules, to cope with degraded reference datasets for mapping the location of selective felling in mixed deciduous forest in Massachusetts using multitemporal Landsat (ETM +) imagery. Klobucar & Pernar ([15]) use MLP and SOM for the estimation and control of the stand stocking based on aerial photographs of the Republic of Croatia. Klobucar et al. ([17]) investigate SOM based image segmentation of color infrared aerial photographs to detect forest damage and determine its spatial distribution. Stümer et al. ([35]) investigate spatial interpolation of in-situ data by SOM algorithms for the assessment of carbon stocks in European forests.
One of the primary goals of FI-based GIS database is data analysis for forest management decision making. Data mining techniques are helpful in the analysis of such large databases. It is an interactive process that requires combining intuition and background knowledge of the problem with the computational efficiency of modern computer technology. For this reason, visualization is a very important part of data mining ([38]). Conventional multivariate statistical methods are not easy to interpret and do not present data from large databases in an easy way to understand ([19], [29], [1]). This is the reason why SOMs are often used in the visualization, analysis and interpretation of databases ([11], [31]). The SOM algorithm is a unique method in that it combines the goals of the projection and clustering algorithms. It can be used at the same time to visualize the cluster in a data set and to represent the set on a two dimensional map in a manner that preserves the nonlinear relations of the data items ([13]).
The amount of data present in modern FI are usually very large and often complex to be analyzed and deeply interpreted. In most cases, FI data are presented in the form of tables and as short text paragraphs, which makes them inappropriate for fast recognition of various deviations or other interesting data patterns. There are numerous techniques of data analysis that can be applied on such data, but none of them can give flawless results of arbitrary data. This is why our purpose was to implement a data transformation with the aim of providing a good starting point for automatic data analysis, and also information in a form suitable for intuitive and easy visual interpretation by human experts. This paper presents a part of our research of NN application in forestry, where we applied Kohonen’s SOM to visualization and analysis of FI at the scale of a stand, management group and management class (see section “Data sets”). The goal is to obtain useful information on the current condition of the forests, as well as an estimation of the forest ecosystem development.
Materials and methods
Study area
The investigated forest area is located in the southern part of the Drava river valley in the Republic of Croatia. It makes part of the management unit “Banov Brod”. Forests of this management unit are ecologically and economically highly valuable natural stands of pedunculate oak, narrow-leaved ash and accompanying species.
Data sets
The Croatian Forest Management Act prescribes how forest management plans should be structured, what they should consist of and how they are verified. The Act defines subdivision of forests into management classes, management class into management groups, and management group into stands. FI of the studied forest area was made during 2008 for a ten-year management period. We have used SOM toolbox 2.0 ([39]) and Matlab 7.9.0 to analyze the management class of pedunculate oak (rotation period: 140 years, area: 364.72 ha without age class 1). This pedunculate oak management class has 40 stands each belonging to the site quality class 2. In our experiments we used two data sets: the whole management class and one management group consisting of all the stands belonging to the age class 6 (age spread 101-120 years).
Management class data have been analyzed first, followed by the age class 6 (20 stands). In both cases the analysis and visualization have been performed at the stand scale (compartments/subcompartments) and 12 stand parameters have been processed: stocking, number of trees per ha (diameter at breast height - dbh >10 cm) - N [ha-1], Basal area per ha - BA [m2/ha], standing volume per ha (dbh >10 cm) - V [m3/ha], current annual volume increment - IV [m3/ha], diameter at breast height of the mean stand pedunculate oak tree - MBD [cm], average stand height of pedunculate oak - [PO-m], percentage of pedunculate oak - [PO-%], number of trees per ha: pedunculate oak [N-po], narrow-leaved ash [N-a], hornbeam [N-h], other tree species [N-o]. The choice of the management class with a relatively small number of stands has been made intentionally so as to make the effects of the SOM-based visualization and clustering evident to the reader. For the same reason, the number of structural parameters has also been limited.
Self Organizing Map (SOM)
SOM belongs to a group of neural networks that use unsupervised learning. The learning process is based on a competitive strategy, where the most successful neuron updates to be even more successful, and the neighboring neurons also get updated but in a lesser degree.
Each SOM consists of a predefined number of neurons, where each neuron has an associated weight vector. The number of elements of each vector is equal to the dimensionality of the input space, in our case the number of the selected stand parameters. During the SOM training phase, distances are calculated between each neuron and a training data sample. The best matching unit (BMU) of a sample is the neuron with the smallest associated distance. BMU gets its weights updated to be closer to the data sample, but to preserve the topology of SOM. Neighboring neurons are also updated towards the sample, though this update is weaker than the BMU’s. The neighborhood is defined with the neighborhood function of SOM as well as the attenuating coefficients that regulate the amount of the update. Through the training process, SOM approaches the probability density function of the training sample and it can be used as its approximation. This is one of the reasons why the final result of SOM training can be easily visualized and interpreted and consequently data visualization is one of the most common uses of SOM. A more detailed description of SOM algorithm is given by Ji ([12]), Giraudel & Lek ([9]), and Kohonen ([19]).
For the visualization and analysis of FI data, we have used label matrix and component plane ([19]) representation of stand structural parameters.
Parameters and size of SOM
Before the training step, the following SOM input parameters have to be defined: number of neurons, topology type, map dimensions and initial weight vectors. We have selected a regular hexagonal topology based on the good practice advice in Kohonen ([19]), which states that the hexagonal lattice should be preferred because final positions of each node depend on more neighbors than is the case with rectangular or triangular regular topologies. The number of neurons and map dimensions influence the final result of SOM training and are usually determined by considering the input data and the primary use of the results. There are no explicit rules for choosing the number of nodes ([29]), but one of the principles is that the size should allow easy detection of SOM structures ([40]). There are several approaches to determine SOM size. Setting the number of nodes approximately equal to the number of input samples seems to be a useful rule-of-thumb for many applications when data sets are relatively small ([14]). Vesanto et al. ([39]) set the number of neurons to approximately 5 x √(number of samples). Hsu & Halgamuge ([11]) use SOMs capable of growth. Kuzmanovski et al. ([20]) use a genetic algorithm. Park & Chung ([29]) set the number of neurons based on an expert advice.
After SOM training, it is important to know whether it has been properly trained or not, because an optimal map for the given input data should be made ([27]). Pölzlbauer ([31]) presents several map quality measures: quantization and topographic error, topographic product, trustworthiness, neighborhood preservation and SOM distortion.
The most commonly used quality measures are quantization and topographic error ([27], [28]). Though quantization error provides information easy to be interpreted, its drawback is that it is decreasing with the increase of the map sizes. This makes it somewhat inadequate, especially when large maps are considered. On the other hand, topographic error measure is unreliable for small maps. Its value is very low with maps that do not contain overly high numbers of nodes. Trustworthiness and neighborhood preservation do not provide one value, but a series of values representing the quality dependent on a parameter. SOM distortion measure cannot be used to compare maps of different sizes, but can be used to benchmark maps of the same size ([31]). Topographic product is a measure of preservation of neighborhood relations in maps between spaces of possibly different dimensionality ([2]). The result of the computation of topographic product indicates whether the map size is appropriate to fit onto the dataset and it can be used to determine the best size of the map for the underlying data set ([31]). Despite its good properties the value of the topographic product depends on the codebook vector initialization.
Currently it is not possible to indicate the best measure of SOM quality, but above mentioned measures may be useful in the selection of SOM parameters ([19]) though they should be selected carefully with the final application in mind. The quality of the map display should generally be evaluated by an expert in the application area ([14]).
In our experiments, we have decided to use the rule of the thumb: approximate number of neurons is set to 5 x √(number of samples). The exact number of neurons is determined when SOM dimensions are set. The ratio of SOM width and height is set to the ratio of the first two eigenvalues of the training set ([39]). In this way the size and topology of the SOM are adapted to the training data set.
To validate our approach for SOM size selection we have considered two primary purposes of the SOM in our experiments: clustering and visualization. Hence, we prefer that similar data samples that are close in the input space remain close in the SOM plane, a property that is usually called “neighborhood preservation”. Quantitative and topographic error are not suitable here, so we turned to trustworthiness and neighborhood preservation measures ([37]). They both compare neighborhoods of each data sample in the input space and the SOM plane, and provide a value in 0-1 range for each data sample. The number of neighboring samples n is a parameter which needs to be set manually and if the closest n neighboring samples of a data sample are the same in both domains, the value returned for the data sample is 1. If one of the closest n neighbors in one domain is not in the n nearest neighbors in the other domain, the return value is decreased depending on the distance rank (which is then higher than n) of the neighbor. The slight difference between the trustworthiness and the neighborhood preservation is in the selection of the primary domain, i.e., the primary domain of trustworthiness is the input space, while the neighborhood preservation uses the SOM plane. We used both measures averaged over all data samples to check the stability and repeatability of neighborhood preservation property for the selected SOM size strategy. Tab. 1 presents trustworthiness and neighborhood preservation values obtained from 5000 simulations (age class 6 data, random SOM initializations, neighborhood size parameter n = 3), confirming the stability of the neighborhood preservation property.
Tab. 1 - Trustworthiness and neighborhood preservation values. Age class 6 data, random SOM initializations, neighborhood size parameter n = 3, 5000 simulations.
| Quality measure | Average value |
Standard deviation |
Min | Max |
|---|---|---|---|---|
| Trustworthiness | 0.90 | 0.02 | 0.79 | 0.96 |
| Neighborhood preservation | 0.90 | 0.04 | 0.72 | 0.98 |
Once trained, SOM can be used for clustering of input data or for classification. In the simplest case, each SOM neuron can be considered as a single cluster or more neurons can be grouped into one cluster. To obtain the input space division, clustering algorithms can be applied to SOM neurons. One can expect that for a trained SOM, all clustering approaches will produce similar results with small differences, so it is difficult to compare them. In the present research, we have decided to use Ward’s and K-means clustering algorithms ([21]).
Results
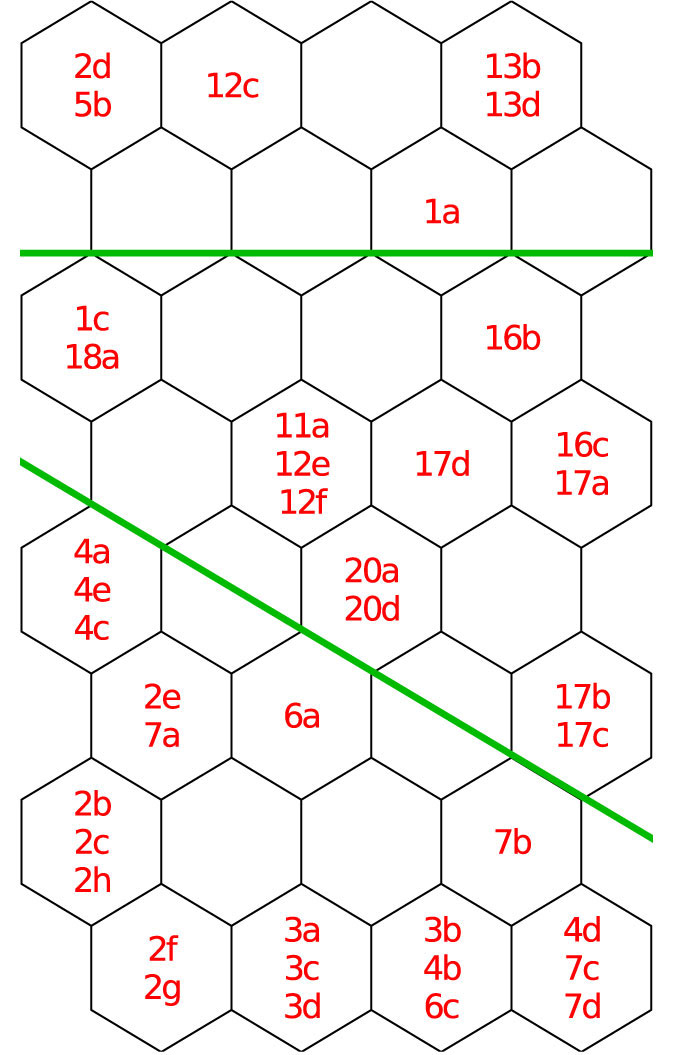
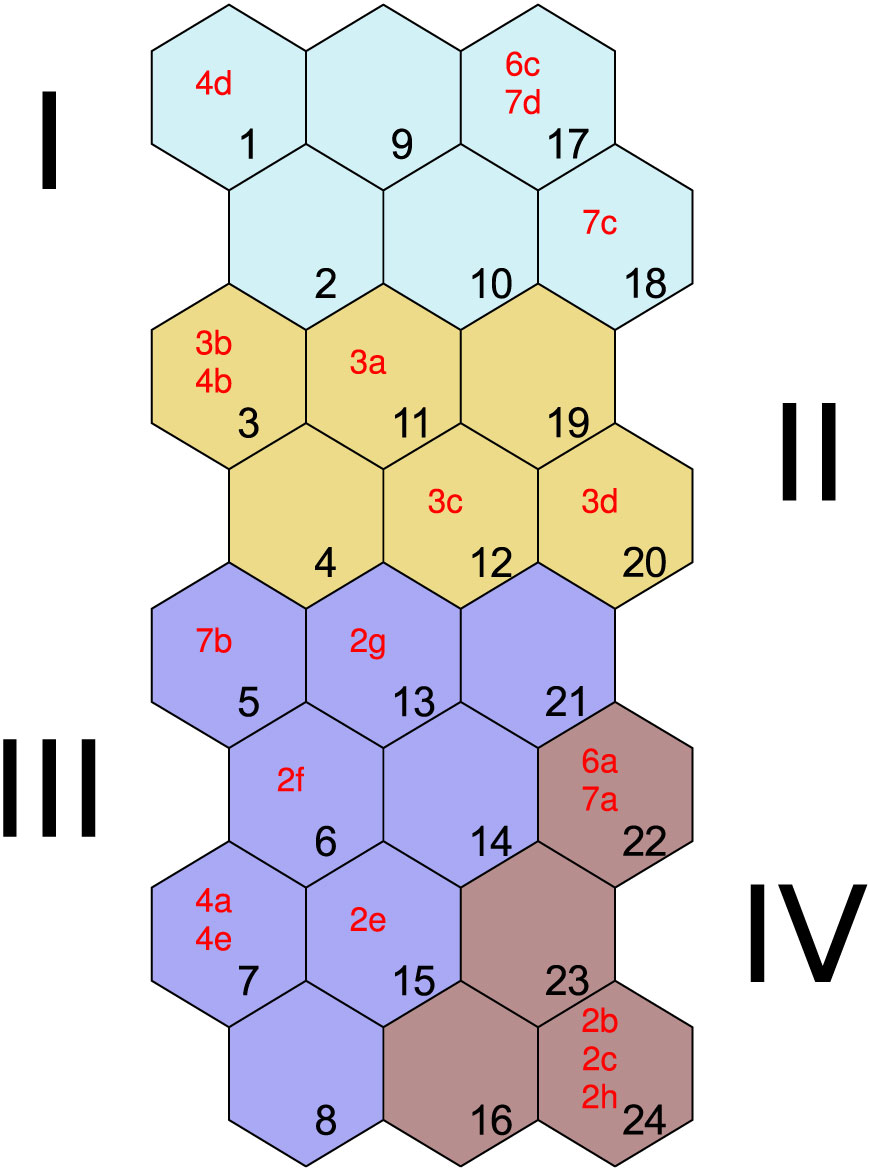
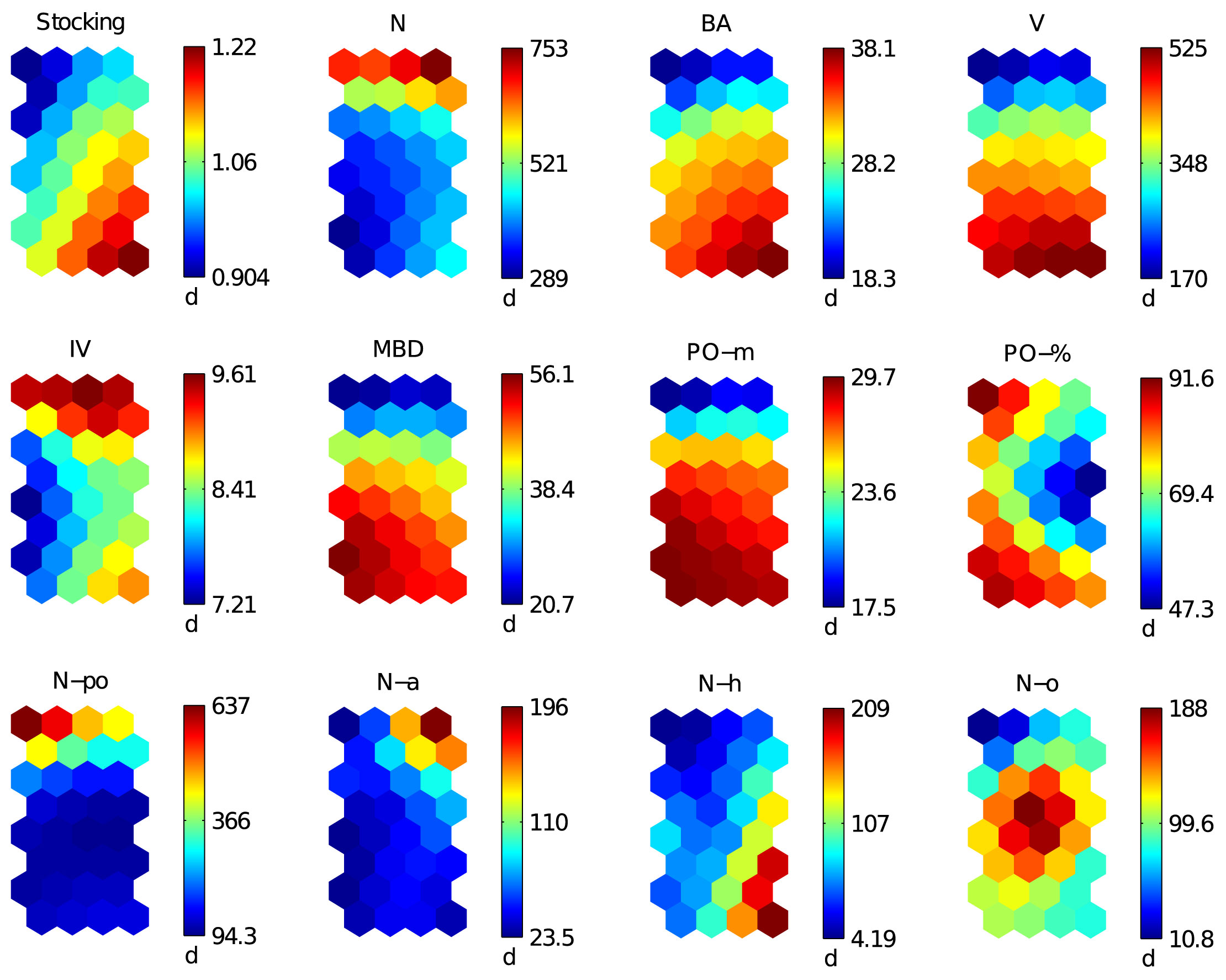
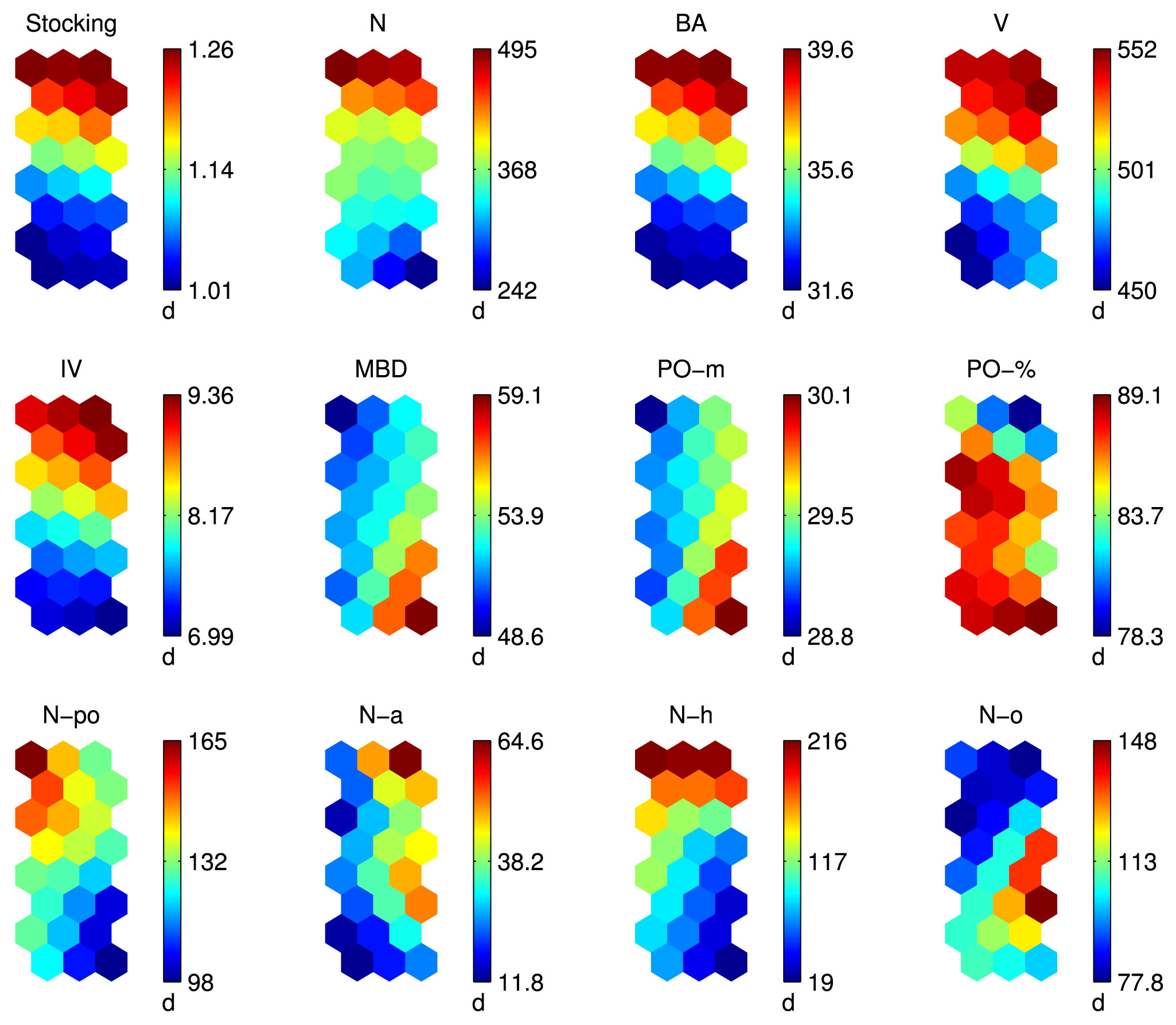
The labels (2d, 5b, 12c etc.) in SOM matrices (see Fig. 1 and Fig. 3) show the “position” of the data samples in the SOM plane. Each data sample is placed into its own BMU. By locating the corresponding BMU in the component plane (see Fig. 2 and Fig. 4), the approximate parameter values for each data sample can be determined. We have applied this principle to visualization and analysis of FI.
Visualization and analysis of management class
In the label matrix (Fig. 1), young stands (age class 2) are located in the upper part, middle aged stands (age class 4) in the middle and old stands (age class 6) in the lower part of the SOM matrix. Such arrangement and clear separation of age classes within SOM matrix proves good clustering and dimension reduction properties of SOM, and also allows further analysis using component plane matrices.
The range and relative relations of stand parameters on the scale of stands and age classes are evident by analyzing component matrices (Fig. 2). One can observe that the stands are of normal stockings (greater than 0.90). The lowest overall number of trees is present in a part of age class 6 stands (lower left) and the largest basal area is present in the other part of age class 6 stands (lower right). Stands of all age classes have satisfactory standing volume per hectare. The current annual volume increment in middle aged and old class stands is 7-9 m3 ha-1, and it is the highest in stands of age class 2 (> 9 m3 ha-1). Average stand heights mostly correspond to the stand age and the site quality class as do the MBD values. The number of trees of narrow-leaved ash is the highest in age class 2 stands (1a, 13b, 13d) and hornbeam is most frequent in age class 4 and 6 stands (lower right). All others tree species are most frequent in age class 4 stands (middle of the SOM matrix).
Pedunculate oak is dominating in the mixture of all age classes with the lowest portion in age class 4 (middle and right part of the SOM matrix). It is evident that the number of trees of pedunculate oak is very low in all stands of age class 4 and part of age class 6 (the number is even lower than suggested by reference literature in the yield tables - [33]). In this example, the information on stands of class 4 and part of age class 6 obtained from SOM component matrices suggests that the applicable forest management plans (i.e., the implementation of adaptive management policies) should be seriously reviewed and changed.
The proposed SOM-based visualization data are usually available in the form of multi-column, multi-page tables in forest inventory databases. Overall information presented in such way is very difficult to grasp and it is difficult to quickly and efficiently identify interesting trends and deviations or even to get a hint that something is not as expected. The proposed SOM-based visualization can provide exactly such interesting information or indices in a fast and efficient manner to an experienced operator. Once a problem or a deviation in a forest ecosystem has been identified, it is easy to extract interesting information in a more detailed form from the numerical data. Another approach could also be the application of SOM-based visualization and data analysis on a smaller scale, as we did in our experiments with a management class and its age class 6.
Visualization and analysis of age class 6
In the label matrix (Fig. 3) locations of all stands can be observed. The analysis of component plane matrices (Fig. 4) points to the relatively large spread of stocking, overall number of trees [N], basal area [BA], volume [V] and increment [IV]. Three groups can easily be identified on the basis of these parameters. The first group consists of stands 4d, 6c, 7c, 7d (higher values); the second group consists of stands: 3a, 3b, 3c, 3d, 4b; the third group consists of stands: 2b, 2c, 2e, 2f, 2g, 2h, 4a, 4e, 6a, 7a, 7b (lower values). Also in the third group, stands can be identified of largest MBD and average stand height [PO-m], and with the lowest number of pedunculate oak [N-po] and hornbeam trees [N-h] (lower right part of the SOM matrix, stands 2b, 2c, 2h, 6a, 7a). This leaves us with four final groups or clusters.
Pedunculate oak is the dominating species (more than 70%) and it is 29-30 m high. Narrow-leaved ash [N-a] is most frequent in stands located in the upper and middle right part of the SOM matrix while hornbeam is most frequent in the first cluster. All other species [N-o] are most frequent in stands 3d, 6a and 7a.
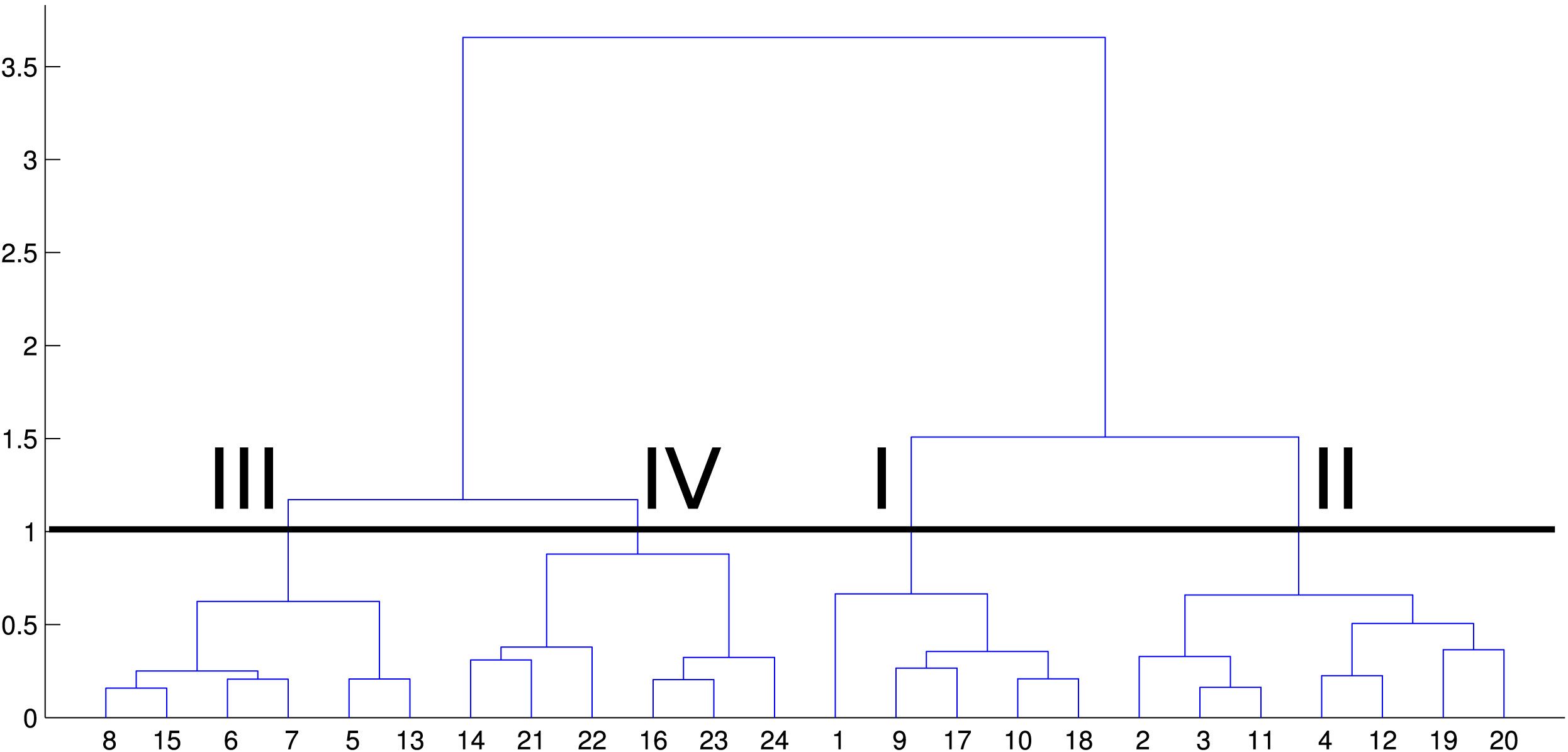
Visual interpretation results are confirmed with the Ward’s and K-means clustering methods. With appropriate parameters, both clustering methods could identify four clusters (Fig. 3 and Fig. 5), and all clusters contain the corresponding stands. With Ward’s clustering, the graph in Fig. 5 shows index values of neurons plotted on x-axis. Stands whose BMUs are indexed can be seen in Fig. 3.
Tukey HSD test indicates the similarity or dissimilarity of clusters depending on the average value of structural parameters (Tab. 2). It can be observed that the first and the second cluster are significantly different compared to the third and fourth cluster. When average structural parameters of each cluster in Tab. 2 are considered, it can be seen that the fourth cluster consists of stands with a low number of pedunculate oak trees, weak volume increment, higher MDB than expected according to the corresponding yield tables. This important information can be easily seen in SOM component matrices and it indicates that the usual management plan is not applicable any more. In our example, it is advisable to start regeneration of these stands immediately, prior to the expiry of the usual 140-year rotation period. For the remaining three clusters, SOM-based visualization also provides useful information. Stands from the third cluster have better structure than the fourth cluster stands, but it is still not entirely satisfactory. This can also be seen in SOM component matrices and it indicates the need for closer monitoring of stands. Stands of the first and second cluster are of much higher quality and no warning signs can be observed in SOM-based visualization, so normal rotation period should be followed for these stands.
Tab. 2 - Tukey HSD test of stands structural parameters. Clusters with the same superscript mark (A, B or C) in one row are considered similar regarding the corresponding stand parameter.
| Stand Parameter |
Cluster | |||
|---|---|---|---|---|
| I | II | III | IV | |
| Stocking | 1.28 | 1.18 | 1.03 | 1.03 |
| N | 502 | 369 | 347 | 276 |
| BA | 40.17 | 36.85 | 32.24 | 32.21 |
| V | 554 | 533 | 457 | 479 |
| IV | 9.45 | 8.62 | 7.42 | 7.22 |
| MBD | 51.28 | 51.92 | 51.20 | 58.82 |
| PO-m | 29.28 | 29.30 | 29.07 | 30.18 |
| PO-% | 79 | 89 | 87 | 86 |
| N-po | 141 | 146 | 127 | 95 |
| N-a | 51 | 25 | 17 | 41 |
| N-h | 226 | 99 | 102 | 16 |
| N-o | 84 | 99 | 103 | 124 |
Component matrices enable visual comparison among structural parameters and their correlation can be easily detected. By visually comparing component matrices of stocking and basal area, stocking and volume, stocking and increment, overall number of trees and increment, basal area and volume, basal area and increment, volume and increment, MBD and height of pedunculate oak, similarity can be easily detected based on color distribution. This indicates that there is significant correlation between two corresponding structural parameters (Fig. 4). Negative correlation can be observed between MBD and number of pedunculate oak trees and between average stand height and number of pedunculate oak trees. In corresponding component matrices, opposite trends can be observed in color/grayscale change (Fig. 4). These visual observations are confirmed by the calculation of correlation coefficients presented in Tab. 3.
Tab. 3 - Correlation coefficient between stands structural parameters.
| Stand Parameter |
Stocking | N | BA | V | IV | MBD | PO-m | PO-% | N-po | N-a | N-h | N-o |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Stocking | 1.00 | - | - | - | - | - | - | - | - | - | - | - |
| N | 0.69 | 1.00 | - | - | - | - | - | - | - | - | - | - |
| BA | 1.00 | 0.70 | 1.00 | - | - | - | - | - | - | - | - | - |
| V | 0.93 | 0.39 | 0.92 | 1.00 | - | - | - | - | - | - | - | - |
| IV | 0.97 | 0.77 | 0.97 | 0.85 | 1.00 | - | - | - | - | - | - | - |
| MBD | -0.34 | -0.62 | -0.35 | -0.09 | -0.40 | 1.00 | - | - | - | - | - | - |
| PO-m | -0.22 | -0.47 | -0.23 | -0.02 | -0.24 | 0.94 | 1.00 | - | - | - | - | - |
| PO-% | -0.36 | -0.69 | -0.37 | -0.09 | -0.47 | 0.07 | -0.12 | 1.00 | - | - | - | - |
| N-po | 0.57 | 0.46 | 0.57 | 0.49 | 0.53 | -0.83 | -0.81 | 0.25 | 1.00 | - | - | - |
| N-a | 0.23 | 0.19 | 0.23 | 0.20 | 0.24 | 0.05 | 0.20 | -0.37 | -0.09 | 1.00 | - | - |
| N-h | 0.56 | 0.83 | 0.57 | 0.29 | 0.59 | -0.55 | -0.47 | -0.54 | 0.40 | -0.23 | 1.00 | - |
| N-o | -0.21 | 0.03 | -0.21 | -0.24 | -0.09 | 0.23 | 0.25 | -0.19 | -0.34 | 0.00 | -0.31 | 1.00 |
Weight vector values of each neuron represent its coordinates in the input space, where each coordinate represents a structural parameter. Data samples are also located in the input space and after SOM training, BMU neuron is appointed to each sample. BMU of any data sample should be located close to the sample. This raises an interesting question: how good is the representation of samples with corresponding BMUs? To answer this question in our case, we have calculated average and standard deviations of distances between BMUs and corresponding data samples for each structural parameter for age class 6 stands (Tab. 4).
Tab. 4 - Average difference of neurons and stands structural parameters. (AD): average distance; (SD): standard deviation.
| Stand Parameter |
AD | SD |
|---|---|---|
| Stocking | 0.03 | 0.02 |
| N | 34 | 25 |
| BA | 0.82 | 0.49 |
| V | 15 | 11 |
| IV | 0.21 | 0.16 |
| MBD | 1.01 | 0.8 |
| PO-m | 0.17 | 0.14 |
| PO-% | 2.84 | 2.08 |
| N-po | 8 | 6 |
| N-a | 23 | 26 |
| N-h | 34 | 39 |
| N-o | 19 | 14 |
Tab. 4 shows that in our experiment differences of BMUs and corresponding data samples are not significant. When compared to FI data, the average distances presented in Tab. 4 are less than 3% for seven structural parameters, for overall number of trees and number of pedunculate oak trees the average distances are between 5% and 10%, and for three parameters (number of accompanying species) the average distances are greater than 10%. These relative ranges are consistent with acceptable error rates in forest management as suggested by [26] (7% for economically highly valuable forest, 10% for medium valuable forest and 15% for forests of low economical value). Such relative errors are acceptable from the forest management point of view. This suggests that SOM neurons (BMUs) can be used to represent the corresponding data samples (i.e., the SOM representation of input data preserves the topology of input data). Consequently, visual analysis and clustering operations performed by SOM neurons can be used for the analysis and clustering of input data. Here, one must be aware that above mentioned distances depend on the number of SOM neurons. Generally, the higher the number of neurons, the smaller the distances, so a good compromise has to be found. Setting the number too high would drive distances towards zero but would also increase the number of calculations and could produce undesired effects for visualization purposes. Once a good enough SOM setup is identified, it can be a valuable tool for data visualization and interactive analysis, dimensionality reduction with topology preserving networks and clustering.
Discussion and conclusion
Decision making management accounting for biological resources and ecosystems constantly confront the problem of predicting the short-term or long term effects of their decisions ([34]). This is the reason why FI has to adapt to the relevant circumstances and obtain useful information for decision making. In forest management a lot of time is spent for data acquisition and processing, leaving little time for decision making. Due to this and the large scale of FI, gathered data must clearly, precisely and efficiently identify all forest management problems. In order to cut down costs and save time, it is a good practice to focus on key parameters describing current condition and development of the forest ecosystem. These are the parameters that can be affected by forest management activities, along with habitat and stand conditions, often indicating the condition of entire forest ecosystem. Such data are necessary for determining how successful and sustainable forest management really is ([3]). Neural networks have demonstrated to be effective to identify data patterns hidden to human experts and conventional methods, and a useful choice for the analysis of complex datasets like FI. The use of SOMs is found to be capable of overcoming most of the limitations encountered in conventional ecological monitoring data analysis methods ([32]). SOM can also be used in the detection of environmental changes, evaluation of ecosystem quality and in the development of ecosystem management policies ([4]).
This paper presents the results of the application of data analysis techniques providing adequate preparation for orderly and timely decision making. SOM application in data visualization and analysis of stand structural parameters enables gathering of holistic information on the current condition of forest stands and development of forest ecosystem. This information is useful for future management and it is necessary for sustainable yield management.
Visual analysis of component matrices proved to be an efficient method to determine relations between structural parameters, as well as to detect individual contributions of structural parameters in forming groups obtained by clustering of SOM neurons. Similar useful properties of SOM, but in different applications, are reported by Park & Chung ([29]) and Annas et al. ([1]).
SOM-based clustering shares the same problems with other clustering methods: accurate identification of cluster boundaries and the definition of the number of clusters. This is usually a problem with complex data such as ecological data, requiring an external assistance to the clustering algorithm. In our study, the number of clusters was determined arbitrarily. However, this has not to be considered a serious disadvantage, because many numerical classification techniques require similar actions. The final classification results need to be evaluated by researchers based on ecological knowledge and research experiences, which cannot be replaced by mathematical methods ([41]). Indeed, many techniques in forestry require a high degree of skill and experience (e.g., decision making in forest management and planning - [24]).
Neural networks such as SOM are not a panacea, still largely depending on the knowledge and skill of the analyst (e.g., in specifying network parameters or group identification - [7]). Repeatability of the method might be a problem with SOM. During the training, the sample units are connected randomly, so with the same dataset, the final Kohonen maps might be different. However, if the learning parameters have been correctly set, the maps will be different, but the relative position of the units will be almost the same ([9]). It should also be noted that the component plane representation of datasets with a large number of parameters may be difficult to interpret.
The SOM performs a nonlinear dimensionality reduction and good clustering, which is a good basis for data visualization results. Other linear or nonlinear techniques for dimensionality reduction do exist, like PCA, Multidimensional scaling algorithms, Sammon mapping, Generative topographic mapping, etc. ([37]), but they have not been considered in this study. Throughout our experiments we have compared SOM results with PCA which proved its worse performances (as expected) due to its linearity.
Despite some problems encountered, the benefits of SOM in our application are far more significant. Our experiments revealed SOM as a useful tool for visualization and analysis of FI data. This technique enables advanced analysis and monitoring of a large quantity of parameters on the scale of stand, management group and management class (if required, also on the scale of management unit and other forest management plans). The obtained information can be used in many ways, while also enabling high creativity. Our experiments were limited to twelve structural parameters, but the technique can be easily extended to a larger number of both qualitative and quantitative parameters. Therefore, we recommend the application of Kohonen’s SOM for visualization and analysis of FI data.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Hrvatske sume Ltd., Croatian National Forestry Agency, Ljudevita F. Vukotinovica 2, 10000 Zagreb (Croatia)
Faculty of Electrical Engineering and Computing, University of Zagreb, Unska 3, 10000 Zagreb (Croatia)
Corresponding author
Paper Info
Citation
Klobucar D, Subasic M (2012). Using self-organizing maps in the visualization and analysis of forest inventory. iForest 5: 216-223. - doi: 10.3832/ifor0629-005
Academic Editor
Marco Borghetti
Paper history
Received: May 15, 2012
Accepted: Sep 14, 2012
First online: Oct 02, 2012
Publication Date: Oct 30, 2012
Publication Time: 0.60 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2012
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 66027
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 54667
Abstract Page Views: 4205
PDF Downloads: 5464
Citation/Reference Downloads: 47
XML Downloads: 1644
Web Metrics
Days since publication: 4863
Overall contacts: 66027
Avg. contacts per week: 95.04
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2012): 16
Average cites per year: 1.14
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Review Papers
Integration of forest mapping and inventory to support forest management
vol. 3, pp. 59-64 (online: 17 May 2010)
Research Articles
Analysis of factors influencing deployment of fire suppression resources in Spain using artificial neural networks
vol. 9, pp. 138-145 (online: 19 July 2015)
Research Articles
The use of tree crown variables in over-bark diameter and volume prediction models
vol. 7, pp. 132-139 (online: 13 January 2014)
Research Articles
Estimation of aboveground forest biomass in Galicia (NW Spain) by the combined use of LiDAR, LANDSAT ETM+ and National Forest Inventory data
vol. 10, pp. 590-596 (online: 15 May 2017)
Research Articles
Comparing land use registry and sample based inventory to estimate forest area in Podlaskie, Poland
vol. 10, pp. 315-321 (online: 23 February 2017)
Commentaries & Perspectives
Benefits of a strategic national forest inventory to science and society: the USDA Forest Service Forest Inventory and Analysis program
vol. 1, pp. 81-85 (online: 28 February 2008)
Research Articles
Identification of wood from the Amazon by characteristics of Haralick and Neural Network: image segmentation and polishing of the surface
vol. 15, pp. 234-239 (online: 14 July 2022)
Research Articles
Analyzing regression models and multi-layer artificial neural network models for estimating taper and tree volume in Crimean pine forests
vol. 17, pp. 36-44 (online: 28 February 2024)
Research Articles
Are we ready for a National Forest Information System? State of the art of forest maps and airborne laser scanning data availability in Italy
vol. 14, pp. 144-154 (online: 23 March 2021)
Research Articles
Making objective forest stand maps of mixed managed forest with spatial interpolation and multi-criteria decision analysis
vol. 6, pp. 268-277 (online: 01 July 2013)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword