Comparative water balance study of forest and fallow plots
iForest - Biogeosciences and Forestry, Volume 5, Issue 4, Pages 188-196 (2012)
doi: https://doi.org/10.3832/ifor0624-005
Published: Aug 02, 2012 - Copyright © 2012 SISEF
Research Articles
Abstract
Increasing pressure on groundwater due to land use change (e.g., afforestation) and future climate change will alter the recharge of groundwater aquifers, causing shifts in water table levels and hence influencing the available groundwater resources. The effect of land use change on groundwater resources has initiated a major scientific debate during the last decades between foresters and experts in water management in Hungary and in several other countries. The aim of this study was to compare water balances of two different vegetation covers, a groundwater dependent oak forest and a nearby fallow area in the Hungarian Lowland. Water balance components for an oak and a fallow plots, exposed to similar weather conditions and with similar soils, were estimated and compared by calibrating the Hydrus 1-D model using measured soil water content and groundwater levels. The difference in the groundwater consumption was analyzed in details during dry and wet growing seasons. Transpiration at the fallow plot was only about two-thirds of that in the oak forest, while groundwater consumption was three times higher in the forest than at the fallow plot throughout the two-year study. During the dry growing season, the proportion of groundwater use from the total transpiration reached up to 90% at the oak plot. According to the model, in the dry growing season in 2007 both vegetation covers relied significantly on groundwater resources, while in 2008 the consumption of groundwater was notably reduced due to the wet weather at both plots.
Keywords
Introduction
The relationship of vegetation cover and groundwater resources has drawn considerable scientific attention over the last decades. Many studies have shown that deforestation by logging or of natural origin (forest fire, wind damage) increased the average runoff from the affected area (e.g., [4]) and afforestation decreased runoff. Similar results were detected in recharge rates and groundwater depth, predominantly in dry regions. In Australia changes of vegetation from woodland to grassland or crops resulted in increases in recharge rates of one to two orders of magnitude ([22]). The changes were largely due to the altered interception loss and the increased water extraction from the root zone. However, results of paired watershed research agreed only on the direction of the changes, not on their magnitude ([2]).
Comparative water balance studies of forest and low vegetation covers have generally shown higher water use of forest cover ([18], [27], [33]). Nachabe et al. ([27]) analyzed the groundwater consumption in a shallow water table environment and estimated the annual ET for a forested area (1320 mm) and for a pasture (700 mm) using detailed soil moisture and water table monitoring. At the same time, a few studies have found negligible differences in evapotranspiration of different vegetation covers (e.g., [32]). The latter study found that, although there were seasonal differences, on an annual basis the drainage below broadleaved woodland did not significantly differ from that below a pasture.
Due to climate change, air temperature is expected to rise significantly during this century ([14]). As a direct consequence of warmer temperatures, the hydrological cycle will undergo changes with accompanying alteration in the rates of precipitation and evaporation. In Hungary, summer temperatures is expected to increase by up to four degrees by the end of this century, while precipitation is likely to increase in winter and decrease in summer ([10]).
The impact of climate change on groundwater resources was reviewed lately by Green et al. ([11]). Although the uncertainty of predictions for change in groundwater recharge rates and discharge is large (e.g., future climate scenarios and groundwater extraction), numerous studies found that groundwater resources appear to be threatened by future climate change due to increased natural and human water demand.
In light of the water balance uncertainties and the increasing pressures on groundwater resources due to future climate change, a comparative water balance study of an oak forest and fallow vegetation plots was initiated in a drought-threatened lowland environment in north-eastern Hungary. Water balance components were estimated by the Hydrus 1-D numerical model ([34]), calibrated on measured soil moisture and groundwater levels.
Our research questions were the following: (1) what is the magnitude of evapotranspiration components in the two different land-uses; and (2) how has groundwater consumption evolved during dry and wet growing seasons?
Materials and methods
Study area
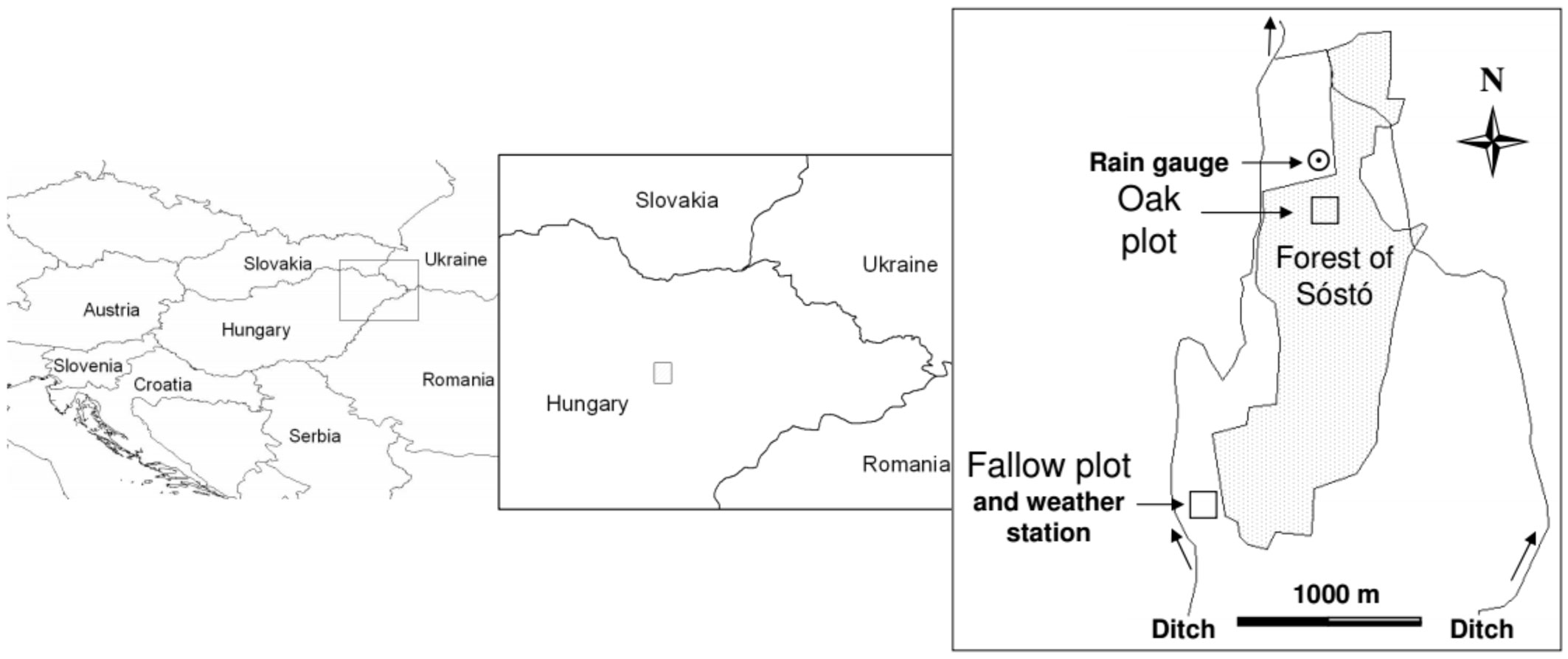
The study plots are situated in the north-east part of Hungary at latitude 47° 58’ N and longitude 21° 42’ E (Fig. 1), built up from sandy river deposits of the early Pleistocene ([3]). The climate is continental; the mean annual precipitation (years 1951-2000) is approximately 520 mm and mean monthly temperature (1951-2000) ranges between -2.4 °C in January and 20.5 °C in July.
The plots were located on the discharge area of the local phreatic groundwater flow system with shallow groundwater levels and groundwater supplies from the adjacent areas. Both study plots were selected so that the elevation of the plots above the nearby ditch was almost the same. The generally similar site conditions of the field plots made it possible to compare water balance components and groundwater consumption. The approximately 300 m distance from the nearby ditch minimized any effect that floods had on water table levels. Surface runoff was not observed since the slope of the plots was less than 2‰ (Tab. 1). For detailed description of the oak plot, see Móricz ([26]).
Tab. 1 - Main field-measured, estimated and calibrated parameter values of the oak and fallow plots. (l): Parameters estimated from literature; (d) parameters estimated from database analysis; (Oak): oak plot; (Fallow): fallow plot.
| Parameter Class |
Parameters | Unit | Oak | Fallow |
|---|---|---|---|---|
| Field- measured |
Height | m | 20-25 | 0.1-0.2 |
| Maximum LAI | m2 m-2 | 3.9 | 1.1 | |
| Free throughfall coefficient | % | 14 | - | |
| Root depth | m | 1.5 | 0.8 | |
| Estimated | Albedod (MODIS data - [16]) |
% | 10-16 (75 at snow cover) |
11-17 (45 at snow cover) |
| Maximum leaf conductancel ([7]) |
m s-1 | 0.0063 | 0.007 | |
| Roughness lengthl ([5]) |
m | 0.9 | 0.026 | |
| Displacement heightl ([8]) |
m | 15.12 | 0.11 | |
| Light coefficient of extinctionl ([7]) |
- | 0.5 | 0.5 | |
| Stem flow ratio of precipitationl ([37]) |
% | 3 | - | |
| Densityd ([28]) |
trees ha-1 | 270 | - | |
| Calibrated | Canopy storage capacity | mm | - | - |
| Vegetation season | - | 1.17 | 1.0 | |
| Dormant season | - | 0.5 | 0.5 | |
| Litter storage capacity | mm | 0.5 | - | |
| Saturated hydraulic conductivity | mm day-1 | - | - | |
| Root-zone | - | 0.9 × 103 2.9 × 103 |
1.5 × 102 1.1 × 103 |
|
| Below the root zone | - | 1.4 × 102 | 0.8 × 102 | |
| Readily available specific yield | - | 0.032 | 0.029 |
The naturally regenerated oak forest had 60% pedunculate oak (Quercus robur) which are 20-25 m high and the density is 270 trees ha-1. The fallow plot, situated about 3 km from the oak plot, is part of an agricultural field that had been plowed in the past, but it has not been seeded and cultivated now for several years and is currently under natural succession. The vegetation consists of furrow-weed with species like Solidago gigantea, Artemisia vulgaris, Amaranthus retroflexus and Ambrosia artemisiifolia.
The vertical distribution of the root system was surveyed in situ by taking three replicate volumetric soil core samples at six depths (0-0.2 m, 0.2-0.4 m, 0.4-0.6 m, 0.6-0.8 m, 0.8-1.0 m and 1.0-1.2 m) for both study plots. After separating the fine roots (diameter < 2 mm) by sieving the soil samples, they were scanned and the total root extent of each sample was determined by grid-counting. Finally, the fine root fraction of each layer was related to the total root extent of the profile. Fine roots reduced approximately linearly with depth at the oak plot (estimated root depth: 1.5 m) and logarithmically at the fallow plot (estimated root depth: 0.8 m).
Soil analyzes included the sieving and hydrometer analyzes of particle size distribution of the soil samples, taken at 0.2 m intervals down to a depth of three meters. At both plots the soil texture was compacted fine sand (0.02-0.2 mm) close to the surface varying between 80-99%. The clay and silt fractions were high below one meter depth at both plots and reach 30-35% and 20-25%, respectively.
Three repetition of undisturbed soil samples for water retention were analyzed at depths of 0.1, 0.3, 0.5, 0.7, 0.9 and 1.2 m by cylinders of 100 cm3 (Tab. 2).
Tab. 2 - Mean of the three measured water retention data of the plots at six depths for five pressure heads. (Oak): Oak plot; (Fall): Fallow plot.
| Pressure | Water content (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 cm | 30 cm | 50 cm | 70 cm | 90 cm | 120 cm | |||||||
| Oak | Fall | Oak | Fall | Oak | Fall | Oak | Fall | Oak | Fall | Oak | Fall | |
| -1 cm | 52.7 | 34.4 | 42.5 | 38.4 | 48.5 | 39.4 | 46.9 | 39.7 | 37.9 | 38.3 | 37.0 | 37.2 |
| -10 cm | 42.8 | 32.6 | 39.0 | 35.0 | 39.7 | 35.6 | 39.9 | 36.7 | 36.0 | 37.7 | 35.6 | 36.8 |
| -333 cm | 20.2 | 19.4 | 20.1 | 19.3 | 17.8 | 23.7 | 22.5 | 30.3 | 32.3 | 30.5 | 23.4 | 33.9 |
| -1000 cm | 16.7 | 15.1 | 16.0 | 14.5 | 15.5 | 18.3 | 18.0 | 22.0 | 25.9 | 22.7 | 16.8 | 26.4 |
| -15000 cm | 7.8 | 10.4 | 7.9 | 9.3 | 7.5 | 11.9 | 7.3 | 14.0 | 14.1 | 14.0 | 9.6 | 17.4 |
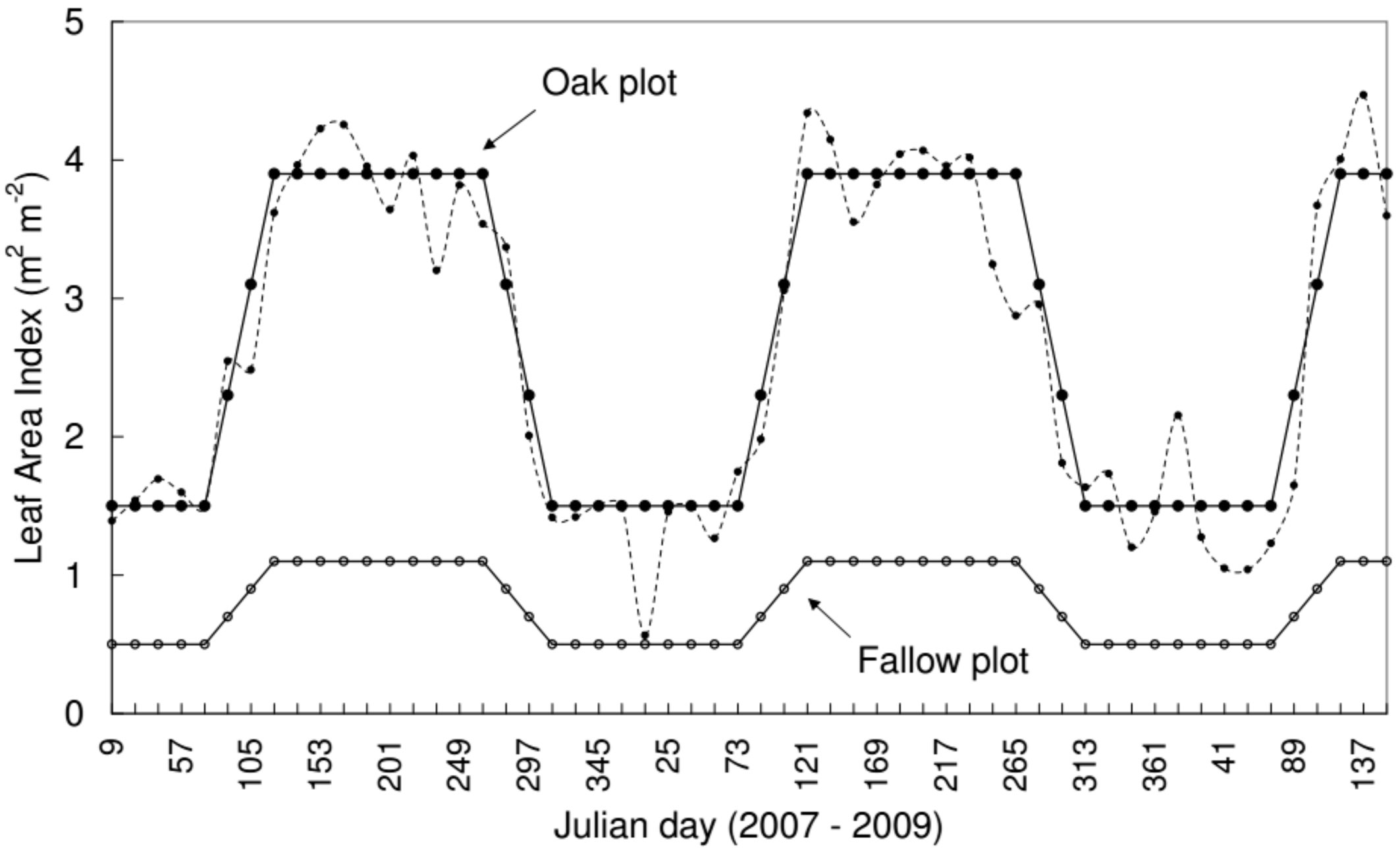
The maximum of the Leaf Area Index (LAI - m2 m-2) was estimated by collecting leaf litter on the ground. At the oak plot, newly defoliated leaves were collected carefully from five locations (1 x 1 m) during late autumn of 2007 and dried in an oven (105 °C for 24 hours). Determination of LAI included the calculation of the ratio of weight to leaf area for a subset of leaves and then for the whole sample. The average LAI of the samples was 3.9 m2 m-2. The 16-day Enhanced Vegetation Index (EVI) product of MODIS (Moderate Resolution Imaging Spectroradiometer) was used to describe the seasonal change of LAI. The 250 m resolution EVI was converted to LAI using the relationship proposed by Wang et al. ([42]).
At the fallow plot, the maximum leaf area index was estimated by leaf collection from three locations (0.5 x 0.5 m). All the collected leaves were scanned and the leaf area was determined by grid counting. The mean LAI of the three samples was 1.1 m2 m-2. The same leaf area index was used throughout the vegetation period. During the dormant season, we assumed the LAI 0.5 m2 m-2, based on the biophysical parameter table of [35] - Fig. 2).
The albedo was derived from the 16-day estimates of the MODIS images. The missing values of albedo in winter were assumed as snow cover and were replaced by an albedo of 45% at the oak and 75% at the fallow plot ([17]).
Monitoring at the plots
Meteorological variables, soil water content and groundwater level were monitored by automatic equipment.
A weather station (iMETOS, Pessl Instruments, Austria) at the fallow plot and an automatic rain-gauge (Rainlog Data Logger, Rainwise, USA) 500 m apart from the oak plot were employed to monitor weather conditions (Fig. 1). The time resolution of rain measurements was 1 minute, while all other variables were recorded hourly.
The volumetric water content was monitored with FDR (Frequency Domain Reflectometers) using Decagon EC-5 probes (Decagon Devices, Pullman, USA) with a time interval of 15 min. The probes were installed at depths of 0.1, 0.3, 0.5 and 0.7 m.
Groundwater level was measured by a Dataqua DA-S-LRB 118 vented pressure transducer (Dataqua Elektronikai Kft., Balatonalmádi, Hungary) with time interval of 15 min. Manual groundwater level measurements were used to verify the reliability of the monitoring.
Water balance modeling with Hydrus 1-D
Model structure
The Hydrus 1-D ([34]) model was applied for the estimation of soil water content changes, actual transpiration and soil surface evaporation at both plots. Hydrus 1-D is a modeling software for analysis of water flow and solute transport in variably saturated porous media. The base of the model is the variable saturated vertical flow domain, where water flow is simulated.
The soil depth was set to three meters at both plots and was partitioned into seven soil layers according to the soil sampling (0-20 cm, 20-40 cm, 40-60 cm, 60-80 cm, 80-100 cm, 100-120 cm, 120-300 cm). The Hydrus model computed the variables of water flow for 200 soil horizons with gradually increments by depth. During the modeling daily time steps were used.
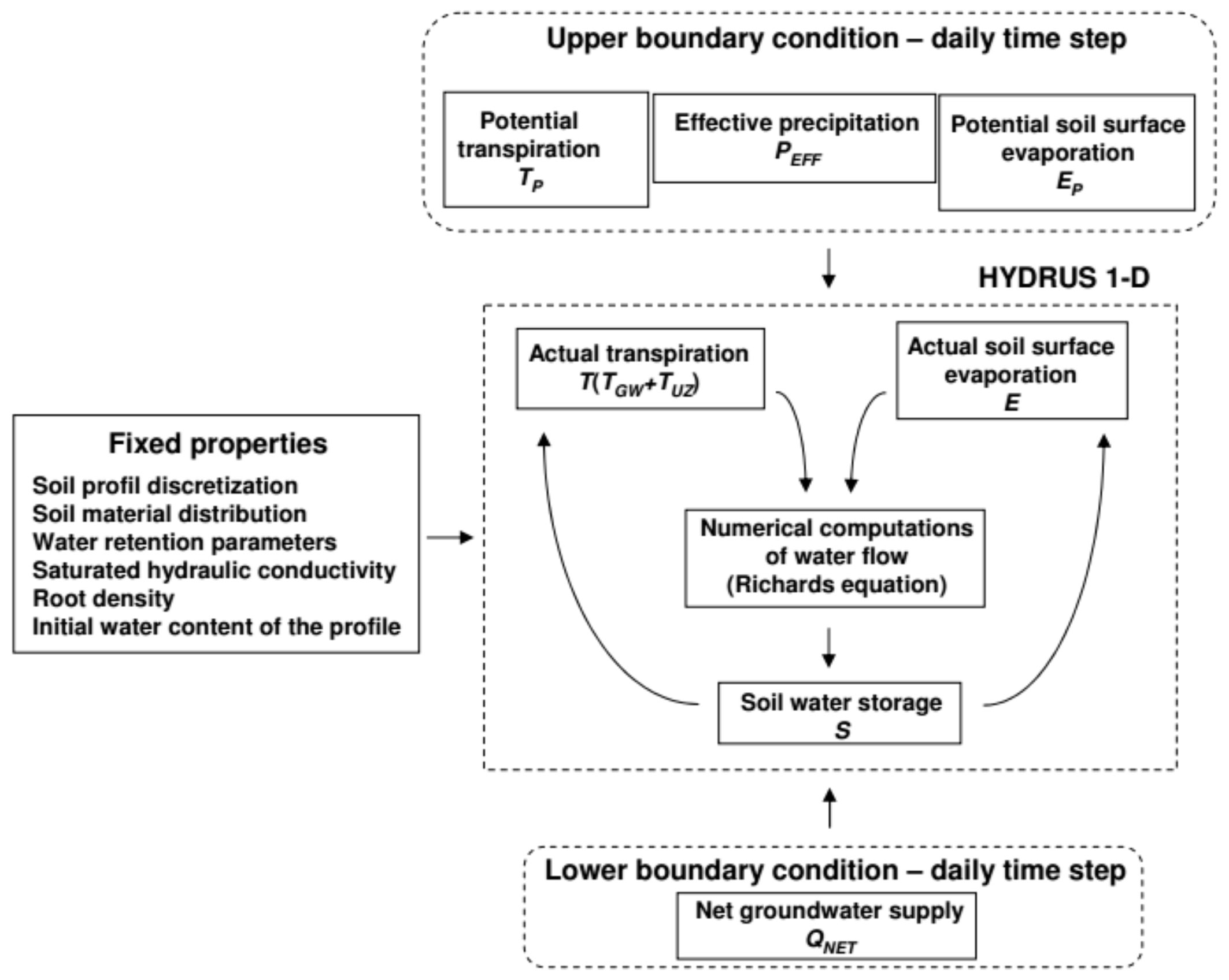
Daily potential transpiration TP (mm day-1) and evaporation EP (mm day-1) values together with the effective precipitation PEFF (mm day-1) constitute the upper boundary condition of the model. PEFF is the difference between the gross precipitation (mm day-1) and the interception loss (mm day-1 - Fig. 3).
Fig. 3 - Structure of the model. (PEFF): effective precipitation; (TP): potential transpiration; (T): actual transpiration; (TGW): groundwater consumption; (TUZ): transpiration from the unsaturated zone; (EP): potential soil surface evaporation; (E): actual soil surface evaporation; (QNET) net groundwater supply; (S): soil water storage. All components are in mm day-1.
The net groundwater supply QNET (mm day-1) defined the water flux at the lower boundary of the soil profile, which was computed using the high-frequency groundwater level data and the readily available specific yield Sy.
Water retention parameters and saturated hydraulic conductivity ks (mm day-1) were put into the Hydrus 1D program for each soil layers. The RETC software ([40]) was employed to get the soil water retention parameters from pairs of water content and pressure head data ([38]). Saturated hydraulic conductivity of the root zone was estimated for every soil layer using the method of Rawls et al. ([30]), although the final values were set by calibration. Root density was assigned to the profile based on field observations.
The actual values of transpiration T and soil surface evaporation E was computed using the potential values, soil hydraulic parameters, the available water content and the root density by the Hydrus 1-D model.
Effective precipitation
Effective precipitation was computed by estimation of the canopy and litter interception loss at the oak plot. The canopy interception loss was calculated applying the Gash model in the growing season (for details, see [9]). Besides the growing season, the daily interception method, proposed by Menzel ([23]) was used to estimate canopy interception loss. The method applies the daily sum of precipitation, the leaf area index and two species-specific parameters, describing the relation between LAI and the storage capacity ([43]) and the slope of the saturation curve ([29]).
Litter storage capacity was set during the model calibration.
Interception loss I was computed by a daily interception method at the fallow plot ([41] - eqn. 1):
where b is the soil cover fraction, which was set to unity since the soil surface was completely covered by vegetation. The empirical parameter ai denotes the storage capacity of the vegetation by multiplying with the LAI (m2 m-2) and P is the daily sum of precipitation (mm day-1).
Potential transpiration and soil surface evaporation
Potential transpiration TP was defined as the canopy transpiration rate, when not limited by soil water deficits ([25] - eqn. 2):
where TP is the potential transpiration (mm day-1), K is the net shortwave radiation (MJ m-2 day-1), L is the net longwave radiation (MJ m-2 day-1), Δ is the slope of the saturation vapor pressure curve (kPa °C-1), γ is the psychrometric constant (kPa °C-1), VPD is the vapor pressure deficit (kPa), ρa is the air density (kg m-3), ca is the specific heat of moist air (kJ kg-1 °C-1), λv is the latent heat of vaporization (MJ kg-1), ρw is the specific heat of air (kJ kg-1 °C-1), Cat is the aerodynamic conductance (m s-1) and Ccan is the canopy conductance (m s-1). Ccan was computed by multiplying the leaf area index by leaf conductance (m s-1).
Leaf conductance Cleaf (m s-1) was estimated after Jarvis ([15]) to express the effect of atmospheric demand on stomatal opening (eqn. 3):
where glmax and glmin are the maximum and minimum leaf conductance (m s-1), respectively, and fT, fD, fR, fW, fC are reduction factors, varying between zero and unity, that account for effects of temperature, vapor pressure deficit, radiation, leaf water stress and atmospheric carbon dioxide concentration on stomatal opening.
The reduction factors fT and fD were computed after Federer et al. ([7]) and Lohammar et al. ([20]). The radiation response fR was estimated after Stewart ([36]) using the measured global radiation. The leaf water stress was omitted, thus fW =1, and the effect of changing atmospheric carbon dioxide was also not considered, so fC =1.
Potential soil surface evaporation EP was also computed by the Penman-Monteith equation, based on the net radiation which reaches the soil surface ([31]).
Net groundwater supply
Diurnal fluctuation of groundwater levels occurs in shallow groundwater regions. The main inducing factor is the diurnal changes of transpiration during vegetation periods ([13]).
Gribovszki et al. ([12]) developed an empirical approach, based on the White-method ([44]) using the observed groundwater level data and the readily available specific yield Sy. The primary assumption was that Qnet displays a significant daily variation due to hydraulic gradient changes over the day. The maximum value of Qnet was calculated for each day by selecting the largest positive time-rate of change value in the groundwater level readings, while the minimum was obtained by computing the mean of the smallest time-rate of change in the predawn hours, by multiplying it by the value of Sy (eqn. 4):
where QNET is the net groundwater supply, h is the groundwater level, t is the time and Sy is the readily available specific yield.
The values of the minimum and maximum Qnet then were assigned to the locations of the groundwater level extremes. Spline interpolation was applied to interpolate the missing values between the minimum and maximum values. The daily sum of the net groundwater supplies was computed by summing up the half-hourly values.
Readily available specific yield was introduced by Meyboom ([24]) to denote the amount of water that can be released from the vadose zone during the time-frame of the daily fluctuations. Sy was estimated from soil texture data using the diagram of Loheide II et al. ([21]). The final values were set during the calibration of the model.
Actual transpiration and soil surface evaporation
Actual transpiration T was computed by integrating the actual transpiration rates of all model layers by the Hydrus 1-D model ([34]). The actual transpiration rate of a specific model soil layer is (eqn. 5):
where Tmsl is the actual transpiration of one specific model soil layer, α(h) is the value of the S-shaped water uptake response function ([39]) and Sp is the potential uptake rate of that soil layer (mm day-1), determined by the vertical root distribution.
Values of the parameter α(h) may be obtained as follows (eqn. 6):
where h is the pressure head (cm), h50 represents the pressure head at which the water extraction rate is reduced by 50% (cm) and p is an experimental constant. The latter was set to three after van Genuchten ([39]) and h50 was set to -4300 cm ([6]).
Sp is calculated using the value of daily potential transpiration and the normalized root water uptake distribution. For more details see Simunek et al. ([34]).
Actual soil surface evaporation E was estimated by the Hydrus model, based on soil water conditions and soil hydraulic properties using Darcy’s Law, bounded by the potential soil surface evaporation.
Model calibration
The observed soil water content and groundwater level data were employed to calibrate the Hydrus model at both plots. The model was calibrated specifically for this two year period and not used for future simulation.
During the model calibration, the storage capacity of vegetation and soil hydraulic parameters were modified to reduce the deviations between the modeled and observed soil water content of each layer and groundwater level.
At the oak plot, first the interception loss of the dormant season was calibrated. The storage capacity of stems and branches was set to 0.5 mm ([19]). Litter storage capacity was generally set to 0.5 mm. Storage capacity of the canopy in the vegetation period was calibrated to 1.17 mm at the maximum LAI 3.9 m2 m-2. A similar result (1.19 mm) was obtained by André et al. ([1]) in an oak dominated stand (LAI = 3.8 m2 m-2).
In the fallow plot, the best fit with the observed soil moisture was achieved by using a storage capacity of 1.0 mm during the vegetation period and 0.5 mm for the period of the dormant season.
During the calibration of the saturated hydraulic conductivity, the initially computed values were modified for the root-zone (<1.5 m at the oak and <0.8 m at the fallow plot) of the soil profile. The calibrated ks values changed between 2.9 · 103 mm day-1 in the upper most horizon and 0.9 · 103 mm day-1 at about 1 m depth at the oak plot. In the saturated zone, the calibrated ks value was around 1.4 · 102 mm day-1 (Tab. 1).
At the fallow plot, the calibrated ks values varied from 1.5 · 102 mm day-1 to 1.1 · 103 mm day-1 in the root zone and around 0.8 · 102 mm day-1 below the root zone.
Readily available specific yield was calibrated to 0.032 at the oak and to 0.029 at the fallow plot.
Model performance
The calibrated soil water content and groundwater levels were compared with measured values at both plots to check the performance of the model. The performance criteria were the coefficient of determination R2, the root mean square error RMSE and the Nash-Sutcliffe modeling efficiency ME.
Results and discussion
Comparison of observed and modeled results
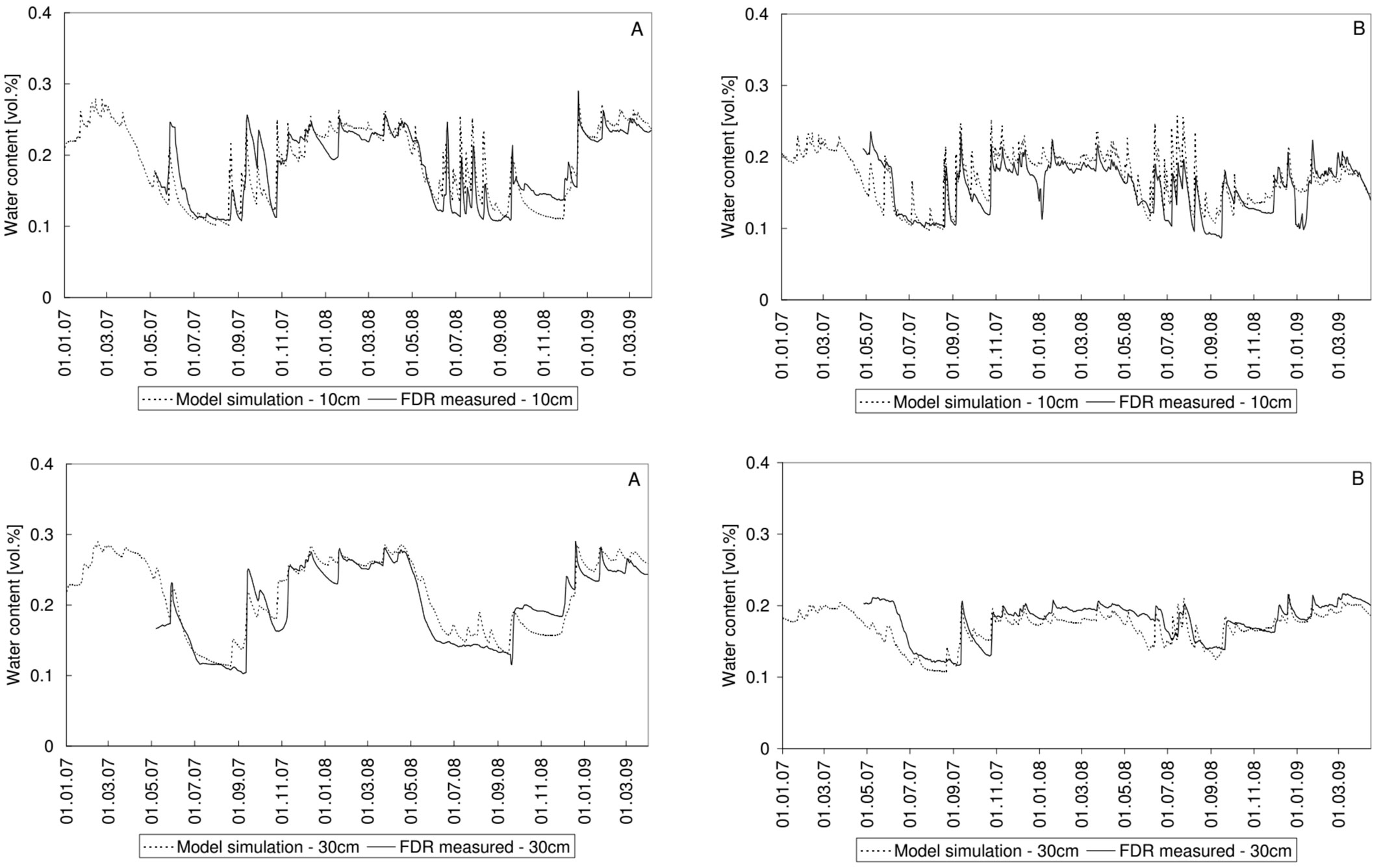
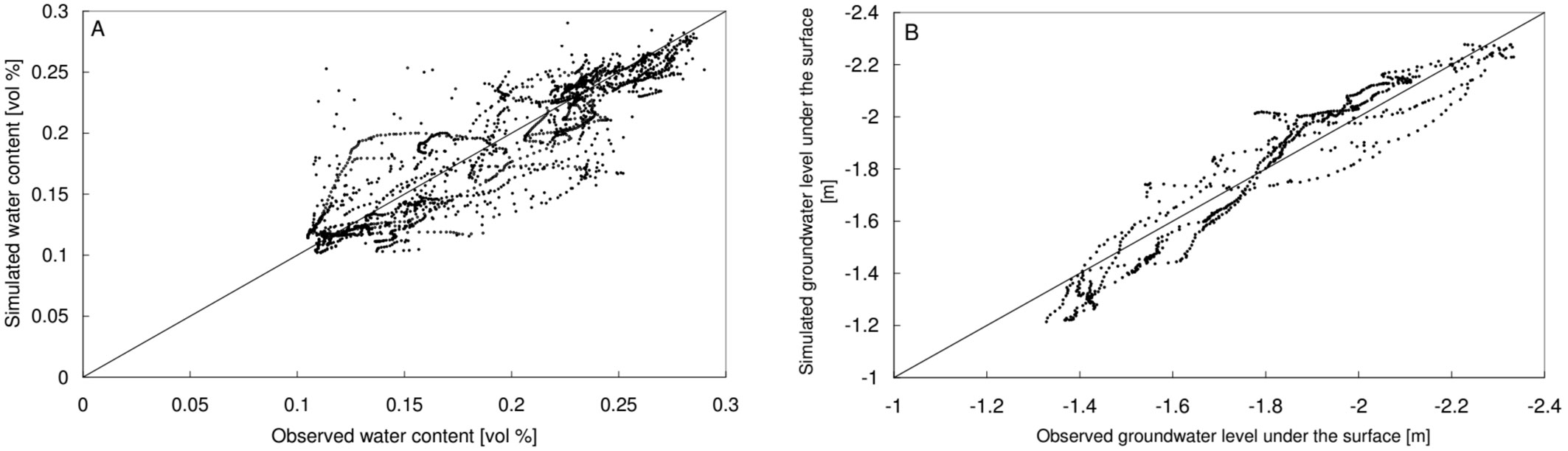
The calibrated soil water contents compared well with observations at both plots (Fig. 4).
Fig. 4 - Comparison of measured and calibrated soil water contents at the oak (A) and fallow (B) plots.
The discrepancies at the beginning of the growing season of 2007 in measured vs. modeled soil water content may be attributed to the disturbance of the soil profile and vegetation at both plots during installation of the monitoring equipment. There were deviations at the fallow plot at a depth of 10 cm in December 2008 and January 2009, due to strong soil water freezing.
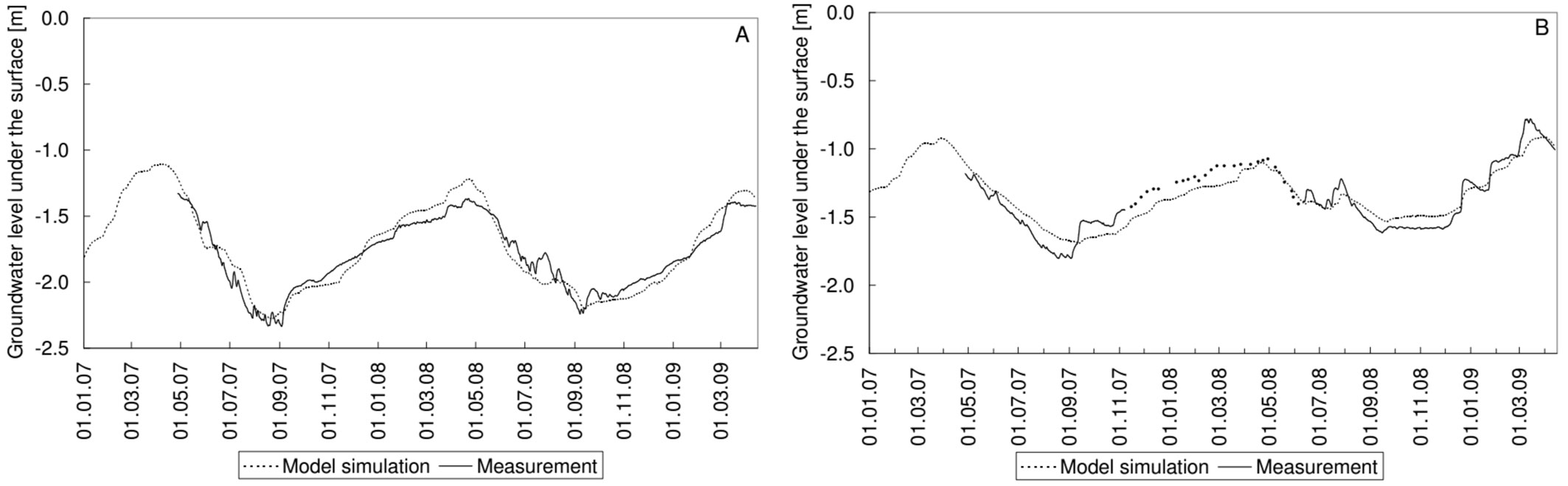
The calibrated groundwater levels compared quite well with measurements at both plots. Due to a malfunction of the pressure transducer, the continuous measurement failed at the fallow plot between November 2007 and June 2008. During this period regular manual groundwater depth measurements were employed to follow groundwater levels at the fallow plot (Fig. 5).
Fig. 5 - Comparison of measured and calibrated groundwater levels at the oak (A) and fallow (B) plots.
Tab. 3 presents the results of the performance criteria.
Tab. 3 - Model performance criteria for soil water content and groundwater levels.
| Plot | Criteria | R2 | RMSE% | ME |
|---|---|---|---|---|
| Oak Plot | Soil water content (10 cm) | 0.727 | 14.91 | 0.690 |
| Soil water content (30 cm) | 0.830 | 11.95 | 0.796 | |
| Soil water content (50 cm) | 0.787 | 13.52 | 0.769 | |
| Groundwater level | 0.921 | 5.03 | 0.883 | |
| Fallow Plot | Soil water content (10 cm) | 0.577 | 16.01 | 0.473 |
| Soil water content (30 cm) | 0.667 | 10.83 | 0.472 | |
| Soil water content (70 cm) | 0.828 | 9.83 | 0.782 | |
| Groundwater level | 0.883 | 5.11 | 0.872 |
Comparison of the measured and calibrated soil water content and groundwater levels showed no systematic divergence at the plots (Fig. 6).
Fig. 6 - Comparison of the daily observed and calibrated soil moisture contents (A) and daily groundwater levels (B) at the oak plot.
Water balance results
Total rainfall interception was twice as much in the forest than at the fallow plot considering the whole study period. In the 2007 growing season, 38% of the rainfall was intercepted at the oak plot, while at the fallow plot it was only 15% of the gross rainfall. As a consequence of more rainfall in 2008, the ratio of interception loss to precipitation decreased slightly at both plots.
According to the Hydrus model, the oak forest transpired approximately 33% more than the fallow vegetation, while groundwater consumption was three times higher during the study period.
Actual soil surface evaporation was only 4% of the total evapotranspiration at the oak plot, and 26% at the fallow plot during the whole study period. The low evaporation amount of the oak plot was the consequence of the high surface resistance due to the litter layer and the shading effect of the canopy. Available net radiation at the soil surface, and soil surface evaporation rates were higher at the fallow plot; thus the soil surface dried out more rapidly than at the oak plot.
Since weather conditions were quite contrasting during the growing seasons of 2007 and 2008, we decided to compare the water balances for both plots from 1st of April until 30th of September.
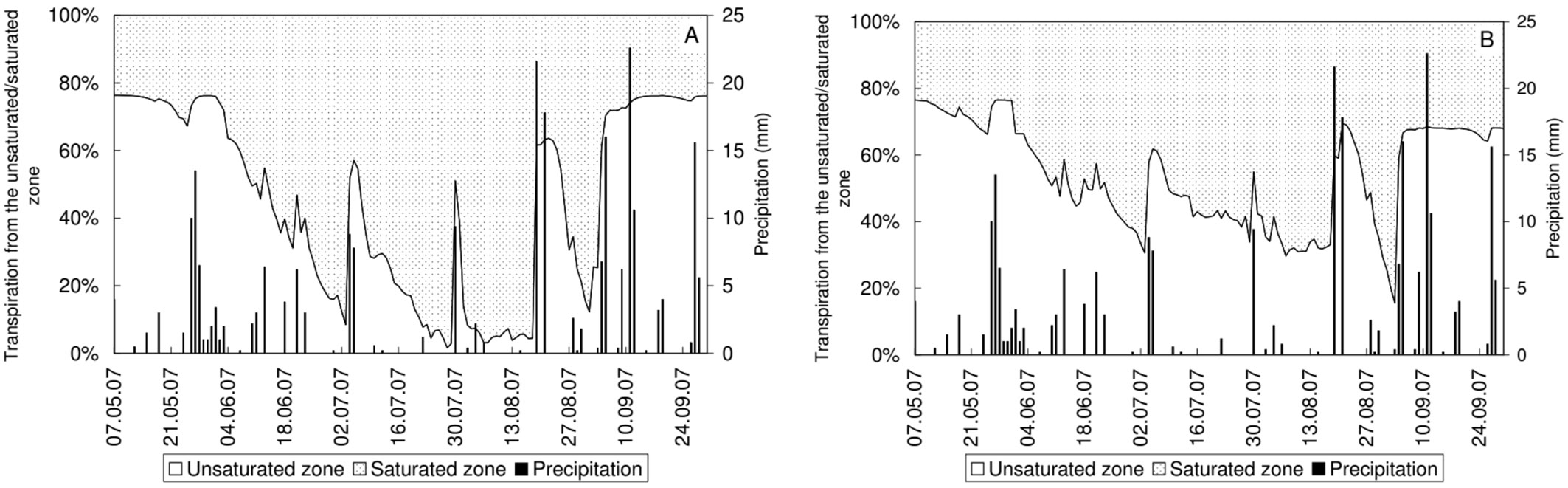
Groundwater consumption TGW was computed using the temporal changes of the capillary fringe in the Hydrus model results, which was 66% of the total transpiration at the oak plot, while at the fallow plot it was only 38% in the growing season of 2007 (Fig. 7).
Fig. 7 - Proportion of the water uptake from the unsaturated and saturated zone and precipitation at the oak (A) and at the fallow (B) plots during the growing season 2007.
In this growing season, the water uptake showed the effect of drought in summer. Until the start of the summer, the transpiration from the unsaturated zone TUZ was considerable from the total transpiration. The fraction of groundwater consumption increased to 60% at the fallow and to 90% at the oak plot in summer.
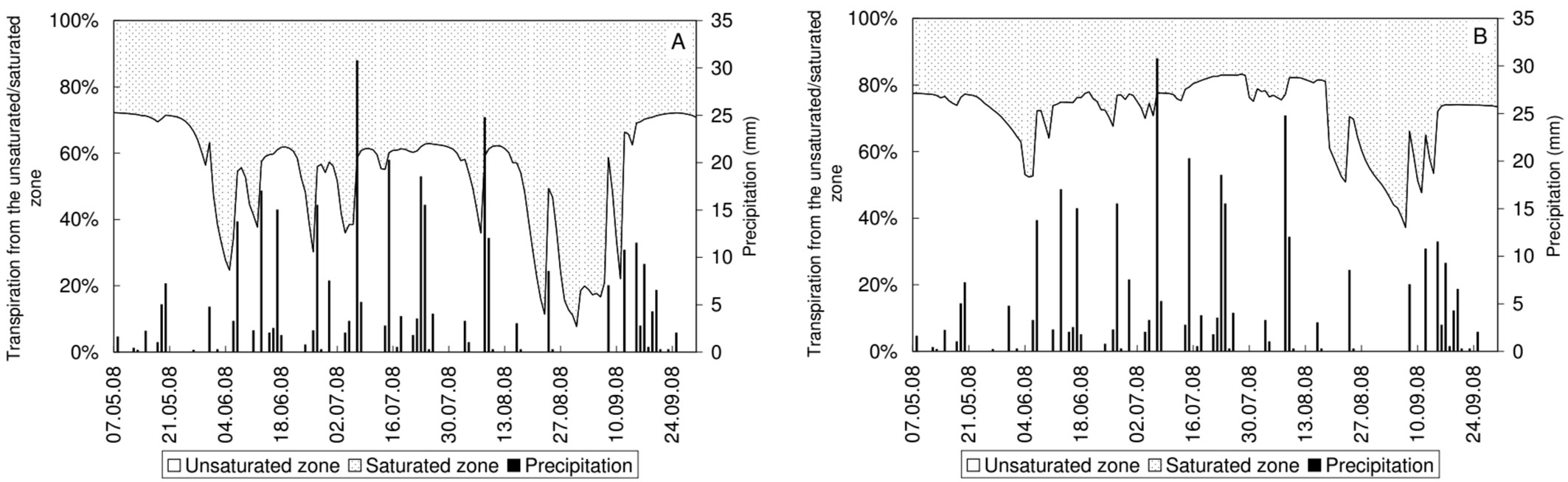
In the growing season of 2008 rainy weather provided a considerable amount of moisture for the unsaturated zone; thus the groundwater consumption was reduced from the preceding year. Groundwater consumption at the oak plot was 50% of the total transpiration, while at the fallow plot it was 25% in the growing season of 2008 (Fig. 8).
Fig. 8 - Proportion of the water uptake from the unsaturated and saturated zones and precipitation at the oak (A) and at the fallow (B) plots during the growing season of 2008.
While in the growing season of 2007 both vegetation covers relied significantly on groundwater resources, in 2008 the evapotranspiration loss of groundwater was reduced considerably due to the rainy weather at both plots.
The water balance components of the growing seasons of 2007 and 2008 are shown in Tab. 4.
Tab. 4 - Water balance components (mm) of the growing seasons of 2007 and 2008 at the oak and fallow plots.
| Water balance components | Growing season - 2007 | Growing season - 2008 | ||
|---|---|---|---|---|
| Oak plot | Fallow plot | Oak plot | Fallow plot | |
| Precipitation (P) | 261 | 261 | 383 | 401 |
| Interception loss (I) | 95 | 39 | 129 | 50 |
| Soil surface evaporation (E) | 22 | 139 | 41 | 154 |
| Transpiration from unsaturated zone (TUZ) | 208 | 235 | 255 | 260 |
| Groundwater consumption (TGW) | 405 | 144 | 255 | 87 |
| Net groundwater supply (QNET) | 289 | 125 | 184 | 55 |
| Change of soil water storage (S) | -180 | -171 | -112 | -95 |
A meteorological tower was not set up at the oak plot, which contributed to the deviations of modeling results from the measurements. Air temperature and relative humidity at the fallow plot were applied above the canopy of the oak forest, which had an influence on the computation of potential transpiration and evaporation.
The empirical approach for computing QNET is further source of uncertainty, since it is sensitive to the quality, the time-step of the record of groundwater levels and the readily available specific yield. The groundwater level data was carefully examined and suspicious measurements were not considered for further computation. The time-step for calculation of QNET was half an hour, considering the 15 min frequency of groundwater level readings, suggested by Gribovszki et al. ([12]). The final value of the readily available specific yield was set to constant despite of its inherent variable nature in space and time.
Conclusions
Water balance components of an oak and fallow plot were estimated from April 1st 2007 to April 1st 2009 by calibrating the Hydrus 1-D model using soil moisture and groundwater level measurements. The study period included a dry (2007) and a wet growing season (2008).
For the entire study period, the Hydrus 1-D model results have shown that the total transpiration of the fallow plot was only two thirds of that obtained in the oak plot, while the soil surface evaporation in the oak plot was approximately one fifth of that in the fallow plot. The separation of transpiration into unsaturated transpiration and groundwater consumption has revealed that the groundwater consumption at the oak plot was almost three times higher than at the fallow plot. The groundwater consumption was close to 60% of the total transpiration at the oak forest and approximately 30% at the fallow plot.
By comparing the dry (2007) and wet (2008) growing seasons, we found that groundwater consumption was approximately 40% less in the wet than in the drier growing season, despite the fact that the groundwater level was deeper during the dry period. Thus, during the dry season both vegetation covers relied considerably on the available groundwater resources.
The results obtained of this investigation reinforce previous reports on higher groundwater consumption of forests as compared to other vegetation covers. Therefore, future afforestation in arid regions with shallow groundwater levels should pay attention to the large groundwater depleting effect of forests, especially in light of future climate change and human water extraction.
Acknowledgments
This research was funded by National R+D (NKFP 3B/2002/012 and NKFP 6-47/2005), EU Joint Development (TÁMOP-4.2.2-08/1-2008-0020 and TÁMOP 4.2.2.B-10/1-2010-0018 “Talentum”) projects and the HAS Bolyai scholarship. The authors would also like to acknowledge NASA for providing the MODIS data free of charge, and anonymous reviewers for providing input to improve the quality of the manuscript.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
C Mátyás
I Berki
E Rasztovits
Institute of Environmental and Earth Sciences, University of West Hungary, Sopron (Hungary)
Institute of Geomatics and Civil Engineering, University of West Hungary, Sopron (Hungary)
Faculty of Geo-Information Science and Earth Observation (ITC), University of Twente, Enschede (Netherlands)
Corresponding author
Paper Info
Citation
Móricz N, Mátyás C, Berki I, Rasztovits E, Vekerdy Z, Gribovszki Z (2012). Comparative water balance study of forest and fallow plots. iForest 5: 188-196. - doi: 10.3832/ifor0624-005
Academic Editor
Marco Borghetti
Paper history
Received: Nov 19, 2011
Accepted: Jun 30, 2012
First online: Aug 02, 2012
Publication Date: Aug 29, 2012
Publication Time: 1.10 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2012
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 59466
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 49543
Abstract Page Views: 3841
PDF Downloads: 4483
Citation/Reference Downloads: 31
XML Downloads: 1568
Web Metrics
Days since publication: 4856
Overall contacts: 59466
Avg. contacts per week: 85.72
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2012): 17
Average cites per year: 1.21
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Groundwater uptake of forest and agricultural land covers in regions of recharge and discharge
vol. 9, pp. 696-701 (online: 17 May 2016)
Research Articles
Links between phenology and ecophysiology in a European beech forest
vol. 8, pp. 438-447 (online: 15 December 2014)
Research Articles
The impact of land use on future water balance - A simple approach for analysing climate change effects
vol. 14, pp. 175-185 (online: 13 April 2021)
Research Articles
Growing season water balance of an inner alpine Scots pine (Pinus sylvestris L.) forest
vol. 11, pp. 469-475 (online: 02 July 2018)
Research Articles
Carbon and water vapor balance in a subtropical pine plantation
vol. 9, pp. 736-742 (online: 25 May 2016)
Research Articles
Use of δ13C as water stress indicator and potential silvicultural decision support tool in Pinus radiata stand management in South Africa
vol. 12, pp. 51-60 (online: 24 January 2019)
Research Articles
Testing a dual isotope model to track carbon and water gas exchanges in a Mediterranean forest
vol. 2, pp. 59-66 (online: 18 March 2009)
Research Articles
Fuel consumption comparison of two forwarders in lowland forests of pedunculate oak
vol. 12, pp. 125-131 (online: 11 February 2019)
Research Articles
Diurnal dynamics of water transport, storage and hydraulic conductivity in pine trees under seasonal drought
vol. 9, pp. 710-719 (online: 21 August 2016)
Research Articles
Variations in the performance of hybrid poplars subjected to the inoculation of a microbial consortium and water restriction
vol. 16, pp. 352-360 (online: 13 December 2023)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword