A comparative fluctuating asymmetry study between two walnut (Juglans regia L.) populations may contribute as an early signal for bio-monitoring
iForest - Biogeosciences and Forestry, Volume 3, Issue 6, Pages 150-152 (2010)
doi: https://doi.org/10.3832/ifor0552-003
Published: Nov 15, 2010 - Copyright © 2010 SISEF
Research Articles
Abstract
Developmental stability, the ability of an individual to eliminate environmental disturbances while expressing a heritable phenotypic trait, was compared in two walnut (Juglans regia L.) populations, a natural and an artificial. Bilateral leaf morphometrics were used to estimate fluctuating asymmetry which refers to random deviation from perfect symmetry of bilateral traits resulting from extrinsic and intrinsic perturbations not buffered during development. Fluctuating asymmetry was used as a proxy of developmental stability. We analyzed our data from a Bayesian perspective showing that developmental stability levels are decreased in the natural population. Our results indicate that an attention may be directed towards the conservation of the natural walnut resources of the area. Fluctuating asymmetry as an indicator of developmental stability may contribute especially in the framework of comparative studies as a population biomonitoring tool.
Keywords
Signal asymmetry, Directional asymmetry, Developmental stability, Bio-monitoring, Conservation
Introduction
Adaptation of organisms to changing environments is becoming a very important issue, especially in the context of climate change. Developmental stability is the ability of an individual to eliminate environmental disturbances while expressing a heritable phenotypic trait. Developmental stability is an important notion for evolutionary and ecological studies, since it provides valuable information on the adaptation of organisms or populations to certain environments. There is evidence that developmental stability has a genetic basis ([1]), nevertheless the relationship between genes and developmental stability is still under debate ([21]).
The lack of data and models does not allow direct estimations of developmental stability. In practice, the pattern of bilateral variation in a random sample of the population, called fluctuating asymmetry ([27], [14]) is widely used as an indirect developmental stability estimator. Fluctuating asymmetry refers to the random deviation from perfect symmetry of bilateral traits resulting from extrinsic and intrinsic perturbations not buffered during development ([27], [14]). Fluctuating asymmetry has been suggested to result from poorly co-adapted gene complexes and therefore to be useful as a measure of developmental stability ([6]). The relation between fluctuating asymmetry and developmental stability is based on the assumption that the symmetric parts of bilateral traits are controlled by the same groups of genes and also that both sides share the same environment, during the process of development. Therefore a perfectly symmetrical phenotype can be expected. During development however, several random errors occur independently and additively in each side introducing a source of uncertainty into the phenotype development mechanism and consequently leading to random deviations from perfect symmetry. The variance of the random deviations (that is equivalent to fluctuating asymmetry) is proportional to the error rate during development. Assuming linear correlation, this variance parameter can be used as an estimator of this error rate and furthermore of developmental stability. Detailed reviews on fluctuating asymmetry are given by Palmer & Strobeck ([15]), Palmer & Strobeck ([16]), Van Dongen ([26]) and Graham et al. ([4]).
There is some underlying additive genetic variance associated with fluctuating asymmetry and relevant QTLs have been identified in poplars ([28]) and mice ([8]), but the extent of its genetic basis remains unresolved ([12], [13], [11], [7], [24]). Nevertheless, there is at least circumstantial evidence that has linked fluctuating asymmetry to environmental stress ([17], [18], [22], [5]) and even to genetic bottlenecks ([6]).
In this study, we compared the fluctuating asymmetry as an indicator of developmental stability in two adjacent walnut (Juglans regia L.) populations: an artificial and a natural. We have estimated fluctuating asymmetry by bilateral leaf morphometrics assuming that leaf asymmetry provides a reliable estimate of the developmental stability in plants and the populations that they belong to. Leaves are highly sensitive tree organs that are subject to environmental, as well as phenological growth cycles and fluctuations ([2]). Our working hypothesis is that comparative developmental stability levels estimated by fluctuating asymmetry provide a cost effective way to obtain insight with regards to population analysis and biomonitoring. Such insight may be valuable for the design of future more thorough studies.
Materials and methods
Sampling
The two populations compared in this study are located in the region of Sohos, near Thessaloniki (Greece) in the area of Mt. Vertiskos at an elevation of 650-700 m (40o 49’ N, 23o 22’ E), characterized by sand-clay soils and typical Mediterranean climate. The region is renown for its walnut and features both wild populations and walnut orchards with trees that attain a height of up to 25 m. The average age of the natural population is about 60 years, however older trees can be found. The artificial population comprises of locally selected genotypes of younger age (40 years old on the average). We chose randomly 29 individuals to sample from each population at a minimum distance of 20 m from each other, avoiding sampling filial structures. Isolated trees (no other tree present at a radius of 100 m) were excluded from sampling. Trees exhibiting natural (infection) or anthropogenic (pruning) disturbance were excluded as well. Ten leaves per tree were randomly selected from lower branches at a height of 2 m, being approximately equally distributed on the circumference of the tree canopy. Measurements were taken after careful drainage.
Analysis
We measured the perimeters of the left (L) and the right (R) side of the leaf in a resolution of 1 mm and used the log-ratio: log(L/R) as Signed Asymmetry (SA) measure per leaf. We were interested to study developmental stability (DS) at the population level, thus fluctuating asymmetry (FA) was estimated using the pooled samples per population. We approached our analysis from a Bayesian perspective. We employed a model to infer SA and Directional Asymmetry (DA - i.e., when one side is systematically larger compared to the other side), similar to the one proposed by Van Dongen ([23], [25], [26] - eqn. 1):
where Yip denotes the i-th SA observation taken from the population p (i.e., natural or artificial); μp corresponds to the expected value of the observation. Deviation from zero indicates the presence of DA in both populations. Otherwise, in case of DA absence, μp should be equal to zero. Parameter σ2FA(p) denotes the variance of SA in the population p (artificial or natural). By using a single parameter for SA per population, we assume that all the trees in each population share a common SA. We used this parameter to observe the developmental stability of the corresponding population. The prior distributions for the parameters in our model are similar to those proposed by Van Dongen ([25]): μp ~ N(0.10) and σ-2FA(p) ~ Γ(0.001, 0.001), where Γ denotes the Gamma distribution. In order to compare the difference in developmental stability between the two populations we estimated the posterior probability (eqn. 2):
We applied Markov Chain Monte Carlo (MCMC) to estimate the probability in eqn. 2 and used the JAGS ([19]) software to perform this posterior simulation. From a total of 120 000 iterations, the first 20 000 were discarded as burn-in stage, while we sampled from the Markov Chain every 100 iterations in order to reduce auto-correlation between samples. Four parallel Markov Chains were simulated and convergence diagnostics were obtained using the CODA R package ([20]). Further inferences were made by combining the samples from the four chains. We used parameter r = σFA(nat) / σFA(art) to monitor the ratio of developmental stability values in the two populations. In addition to our Bayesian analysis, we tested the hypothesis that the variances between the two populations are equal by performing a F-test with null hypothesis H0: σ2FA(nat) = σ2FA(art) and alternative H1: σ2FA(nat) > σ2FA(art) and using the statistic r2 = σ2FA(nat) /σ2FA(art).
Results and Discussion
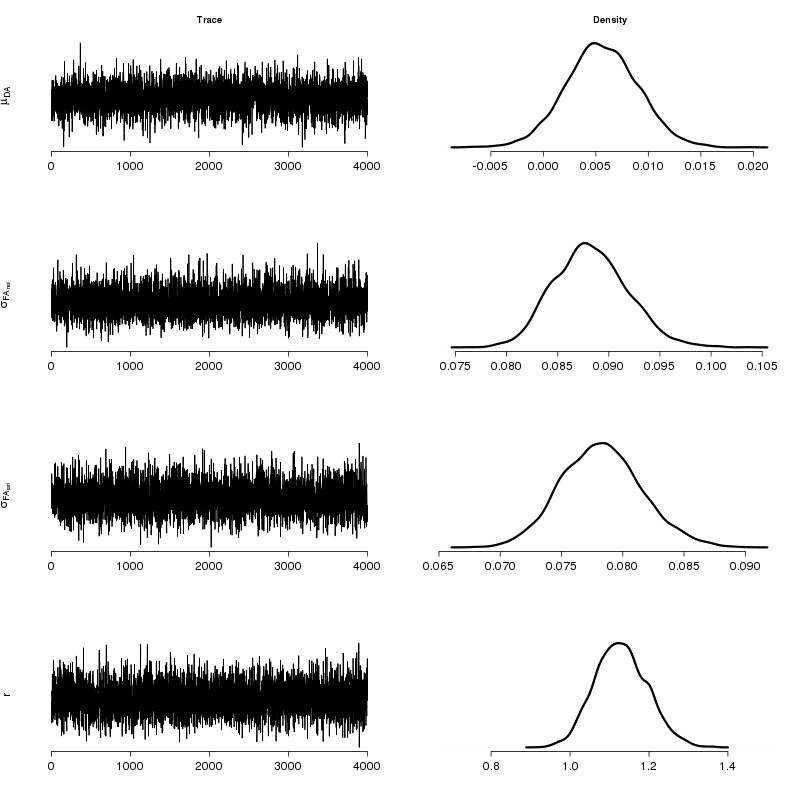
Summary statistics and posterior densities are shown in Tab. 1 and Fig. 1 respectively. Fluctuating asymmetry in the natural population is larger than the fluctuating asymmetry in the artificial, with a probability of 0.982. This result is also supported by the F-test (test statistic r2 = 1.27) resulting to p-value = 0.021 (with the classical statistics interpretation) with confidence intervals CI = (1.047, +inf). We regard this outcome as noteworthy. Our results show that the right side of the leaf is slightly larger than the left side, but still the difference is small and additional experimentation is needed to further elucidate this finding. The natural population can be regarded as presenting reduced levels of developmental stability. It is noted that a significant amount of genetic erosion has been indicated for European J. regia populations and while genetic diversity parameters for northern Greek populations were higher that the average, they were notably lower than typical values reported for widespread plant species ([3]). The artificial population has been long cultivated for the production of regionally renowned walnuts. Nevertheless, any positive influence of cultivation activities on the artificial population does not apply to the adjacent natural population that may be more prone to environmental perturbations and stochastic fluctuations of effective population size. In this case, our results may call for more detailed genetic studies in order to investigate the evolutionary potential of the natural population (genetic monitoring).
Tab. 1 - Summary statistics for the posterior densities of parameters. Column Mean denotes the posterior mean. SD is the standard deviation. The last four columns show quantiles for each variable.
| Parameter | Mean | SD | 2.50% | 25.00% | 50.00% | 75.00% | 97.50% |
|---|---|---|---|---|---|---|---|
| DA (·10-3) | 5.57 | 3.45 | -0.93 | 3.33 | 5.54 | 7.86 | 12.71 |
σFA (nat) | 0.088 | 0.004 | 0.082 | 0.086 | 0.088 | 0.090 | 0.096 |
σFA (art) | 0.079 | 0.003 | 0.072 | 0.076 | 0.079 | 0.080 | 0.085 |
| r | 1.128 | 0.066 | 1.010 | 1.081 | 1.126 | 1.174 | 1.261 |
Fig. 1 - Traces and posterior densities for the parameters of interest. Plots were produced by concatenating the four MCMC chains.
We consider our findings as a potentially early warning indication for problems that may occur in the natural population under scenarios of future environmental uncertainty. Given that expression of both sides of a leaf bilateral trait is due to the same genes, then any asymmetry between the sides can be a consequence of environmental disturbance. Hence, fluctuating asymmetry could be considered as a proxy for environmental or genetic stress ([27], [14]). Our approach is characterized by simple data collection, while a thorough analysis can be streamlined by specific software that we plan to develop. Therefore the careful application of such an approach can present an additional tool to a battery of available applications for population bio-monitoring ([10], [9]). Natural biodiversity is extremely important and it may be vital for biomonitoring and conservation policies to take into account the contribution of simple potential “signals”.
Acknowledgements
Two anonymous reviewers are thanked for their constructive comments and suggestions.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Biometris, Wageningen University and Research Center, Wageningen (The Netherlands)
Laboratory of Forest Genetics and Tree Breeding, Faculty of Forestry and Natural Environment, Aristotle University of Thessaloniki, Thessaloniki (Greece).
Corresponding author
Paper Info
Citation
Kourmpetis YAI, Aravanopoulos FA (2010). A comparative fluctuating asymmetry study between two walnut (Juglans regia L.) populations may contribute as an early signal for bio-monitoring. iForest 3: 150-152. - doi: 10.3832/ifor0552-003
Paper history
Received: Jul 10, 2010
Accepted: Sep 22, 2010
First online: Nov 15, 2010
Publication Date: Nov 15, 2010
Publication Time: 1.80 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2010
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 56187
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 48151
Abstract Page Views: 3108
PDF Downloads: 3544
Citation/Reference Downloads: 10
XML Downloads: 1374
Web Metrics
Days since publication: 5512
Overall contacts: 56187
Avg. contacts per week: 71.36
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2010): 3
Average cites per year: 0.19
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Technical Reports
Conservation and use of elm genetic resources in France: results and perspectives
vol. 13, pp. 41-47 (online: 03 February 2020)
Research Articles
Leaf morphology of progenies in Q. suber, Q. ilex, and their hybrids using multivariate and geometric morphometric analysis
vol. 11, pp. 90-98 (online: 31 January 2018)
Commentaries & Perspectives
The genetic consequences of habitat fragmentation: the case of forests
vol. 2, pp. 75-76 (online: 10 June 2009)
Research Articles
Networking sampling of Araucaria araucana (Mol.) K. Koch in Chile and the bordering zone of Argentina: implications for the genetic resources and the sustainable management
vol. 2, pp. 207-212 (online: 22 December 2009)
Review Papers
Genetic diversity and forest reproductive material - from seed source selection to planting
vol. 9, pp. 801-812 (online: 13 June 2016)
Technical Reports
Population genetic structure of Platanus orientalis L. in Bulgaria
vol. 4, pp. 186-189 (online: 11 August 2011)
Editorials
Workshop COST E52 “Evaluation of beech genetic resources for sustainable forestry”
vol. 2, pp. 104 (online: 10 June 2009)
Review Papers
Implementing the dynamic conservation of elm genetic resources in Europe: case studies and perspectives
vol. 8, pp. 143-148 (online: 07 August 2014)
Research Articles
Delineation of seed collection zones based on environmental and genetic characteristics for Quercus suber L. in Sardinia, Italy
vol. 11, pp. 651-659 (online: 04 October 2018)
Research Articles
Comparison of genetic parameters between optimal and marginal populations of oriental sweet gum on adaptive traits
vol. 11, pp. 510-516 (online: 18 July 2018)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword