Comparison of wood volume estimates of young trees from terrestrial laser scan data
iForest - Biogeosciences and Forestry, Volume 10, Issue 2, Pages 451-458 (2017)
doi: https://doi.org/10.3832/ifor2151-010
Published: Apr 04, 2017 - Copyright © 2017 SISEF
Research Articles
Abstract
Many analyses in ecology and forestry require wood volume estimates of trees. However, non-destructive measurements are not straightforward because trees are differing in their three-dimensional structures and shapes. In this paper we compared three methods (one voxel-based and two cylinder-based methods) for wood volume calculation of trees from point clouds obtained by terrestrial laser scanning. We analysed a total of 24 young trees, composed of four different species ranging between 1.79 m to 7.96 m in height, comparing the derived volume estimates from the point clouds with xylometric reference volumes for each tree. We found that both voxel- and cylinder-based approaches are able to compute wood volumes with an average accuracy above 90% when compared to reference volumes. The best results were achieved with the voxel-based method (r2 = 0.98). Cylinder-model based methods (r2 = 0.90 and 0.92 respectively) did perform slightly less well but offer valuable additional opportunities to analyse structural parameters for each tree. We found that the error of volume estimates from point clouds are strongly species-specific. Therefore, species-specific parameter sets for point-cloud based wood volume estimation methods are required for more robust estimates across a number of tree species.
Keywords
Mixed Forests, Quantitative Structure Models, Voxel-based, Xylometry
Introduction
Biomass and primary production are important key variables in the analysis and study of forest ecosystems ([39], [9]). For the precise determination of woody biomass an exact quantification of the volume and the wood density of the individual trees is required. This is a complex task, given the large variety of tree species and their structural differences. While wood density may be derived relatively easily by using increment borers ([19]), measuring the volume is often more difficult. Traditional methods for wood volume estimations, such as allometric functions, are mostly derived from measurements of the diameter at breast height (DBH) and tree height (TH - [38]) coupled with harvesting and weighing of the observed trees. In monocultures with well studied species those allometric estimates can perform well ([35]), especially in mature stands. However, allometric equations that were developed in pure stands are less reliable in mixed forest stands with different tree ages and more complex structures. In such cases the exact equations may simply be unknown, and using mean allometric equations may be too vague or even misleading ([36], [17]). In addition, many studies deal with large sample sizes which adds further complexity and variation. Therefore, efficient methods for measuring biomass for a large number of trees are desired.
To overcome these challenges airborne or spaceborne remote sensing approaches are typically used to estimate biomass on a global or regional scale ([24]). For small scale applications, up to the plot or individual-tree level, terrestrial techniques are preferable as they allow to measure within the stand. To avoid destructive approaches to get values for wood volume, and ultimately biomass, terrestrial laser scanning (TLS) can be applied. TLS (also referred to as terrestrial lidar) is a well established non-destructive surveying technique that allows to capture fully three-dimensional (3-D) point clouds representing trees ([23]) with a high precision and spatial resolution. Photogrammetric approaches, e.g., hand-held or UAV-based digital camera systems in combination with multi-image matching techniques, may also be used to derive such point clouds as a lower cost alternative ([34]). 3-D cameras (also called range imagers) measuring a distance value for each camera pixel by time-of-flight measurement techniques ([37]) are another alternative for capturing 3-D point clouds. In the near future, the techniques will even be available in smartphones, and solid state lidar devices will depict another option for compact low-cost 3-D point cloud data acquisition.
Over the past decade a number of methods have been developed to derive common tree inventory parameters, such as DBH, TH, ground diameter (GD), and crown radii, from TLS point clouds in an automated or semi-automated fashion ([50], [32], [46], [29], [48]). The extraction of wood and crown volumes, as a more complex task, has specifically advanced over recent years ([42], [5], [30], [22], [33]). However, there are currently no commercially available software packages that deliver wood volumes from TLS point clouds in mixed stands. One reason is that available methods of wood volume calculation from point clouds cannot be applied easily across multiple species and tree sizes. Most methods rely on several input parameters and are still an active field of research. In many cases an advanced knowledge of the respective method is required.
In the literature several methods are described that utilize 3-D voxels grids to compute volumes of trees ([18], [26], [5]). Although there are methodological differences among them, they are similar in the sense that they mostly need just one input parameter, the voxel size. An advantage of the voxel-based methods is that they can account for real stem shapes with irregularities and thus are not limited to symmetrical shapes (e.g., cylinders), which are used in many geometric-model based approaches ([2]). A disadvantage is that heavily occluded branches are often not fully recovered and their volume may be biased.
The other major group of modeling approaches comprises methods which produce quantitative structure models (QSMs). These methods fit geometric primitives into isolated point clouds of trees. The resulting hierarchical collection of cylinders is based on segmentation of the point cloud into individual tree parts (stem and branches). An advantage of these methods is that they can directly deliver the tree topology (branching structure and order) from the local connectivity of the segmentation. Also occlusion is less problematic because the symmetry of the fitted shapes can account for missing points. Reported QSM producing methods, or methods with the capability to produce QSMs within literature can be classified into four different general approaches. A wide range of methods ([52], [31], [10], [13]) relies on Dijkstra’s Algorithm ([14]) to extract the skeleton of a tree which can serve as a basis for the cylinder fitting. Other tree-skeletonization methods which could replace Dijkstra’s algorithm are reported as well ([7], [8], [51]). The second approach relies on segmentation of the point cloud into branches using neighborhood structure of small subsets of the point cloud ([42]). Some other methods utilize search spheres recursively to follow the tree architecture from the root of the tree to its tips and connect fitted circles on the sphere-surfaces to cylinders ([27], [20], [28]). Lastly one method fits directly ellipses into the cloud by utilizing principal curvature and principal directions of each point ([1]).
The motivation of this study was to compare three available methods, one voxel-based and two cylinder-fitting techniques ([42], [5], [20]), and to analyze which of these methods are practical and able to compute reliable wood volume estimates across a range of tree species. For this test we quantified and compared volume estimates from TLS-derived point clouds of young trees of different species. Most of the above TLS-based studies have been shown to deliver acceptable estimates of wood volumes, but so far not many have been tested on the same set of tree samples. We focused on younger trees because they are often missed or under-represented in the analysis of mixed forest stands ([4], [40]), despite their great ecological relevance. As noted by Ashcroft et al. ([3]) most studies of trees with TLS are biased towards forestry and less focused on ecological applications. Planted forest biodiversity experiments, e.g., BIOTREE ([45]) or BEF-China ([6]), that mainly consist of young trees will also benefit from this study. To validate the estimates we used xylometric measurements of harvested trees.
Material and methods
Target trees and study sites
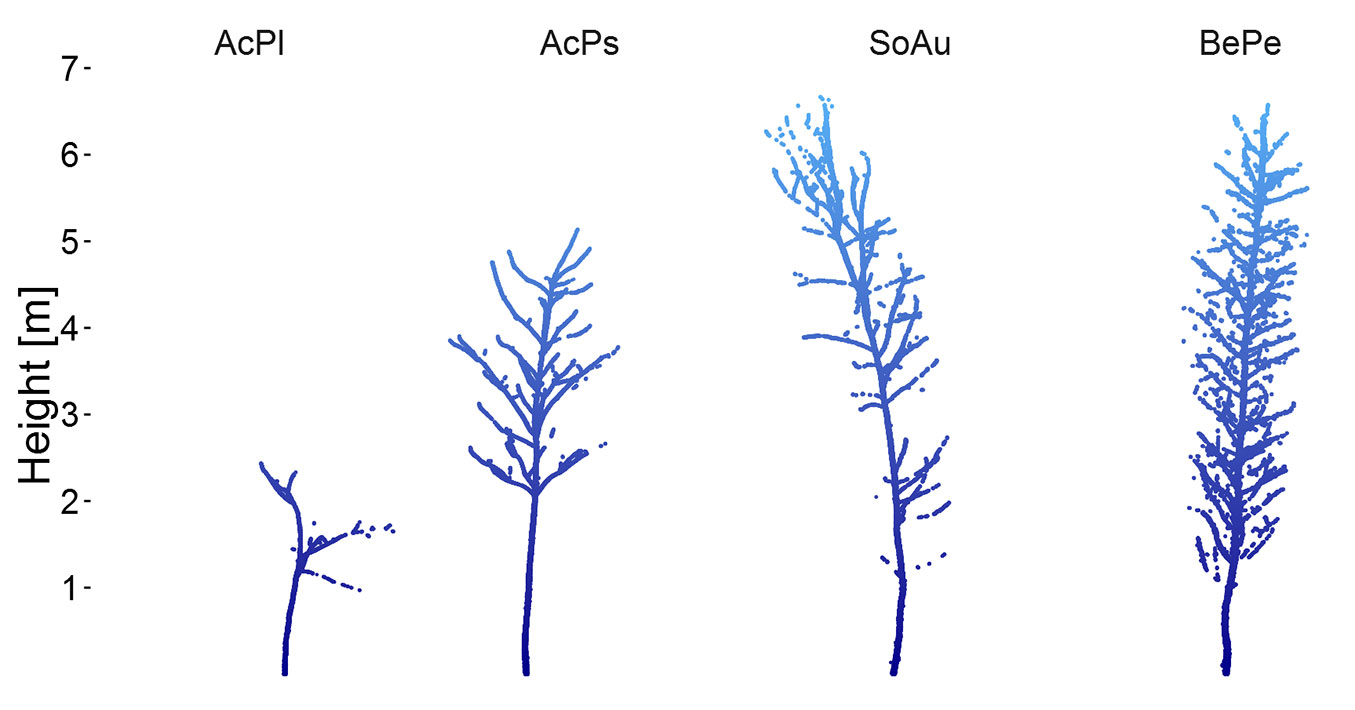
For our analysis we selected data from two different scan campaigns. From Hess et al. ([25]) we used point clouds from 18 trees that were scanned and harvested from a forest in Enzen (52° 19′ 16″ N, 09° 09′ 47″ E), Lower Saxony, Germany. In addition, we included point clouds of six trees from Bienert et al. ([5]) that were scanned and harvested from a forest in Adendorf (53° 17′ 00″ N, 10° 27′ 00″ E), Lower Saxony, Germany. In total 24 trees were selected comprising of four species: Acer platanoides L. (AcPl, Norway maple), Acer pseudoplatanus L. (AcPs, Sycamore maple), Sorbus aucuparia L. (SoAu, Rowan), and Betula pendula ROTH (BePe, Silver birch). The trees were selected based on the following criteria: (i) understorey trees that stand in groups; (ii) height between 1.3 m and 8 m; (iii) different structural habitus and species. Their structural complexity, that is the number, length and mid-diameter of branches of different branch order and the crown shape, increases in the following order: AcPl < AcPs < SoAu < BePe (Fig. 1). This classification was based on diameter and length differences at the different branch order levels of each species as well as on four simple crown variables measured from the point clouds (for details see [25]). For each tree DBH, TH, and age data was available from conventional measurements, as well as a xylometric measurement of wood volume (see below) after scanning and cutting. DBH was measured using a diameter tape with 0.1 cm resolution. TH was measured with measurement tapes as the length of the chopped trunk. Tree age was determined by counting tree rings of a near ground stem disc under a lab microscope. DBH ranged between 1.1-4.5 cm, TH between 1.79-7.96 m, and tree age between 7 and 16 years (see Tab. 1).
Fig. 1 - Representative sample point clouds of the four species in this study. Species abbreviations refer to Acer platanoides (AcPl, Norway maple), Acer pseudoplatanus (AcPs, Sycamore maple), Sorbus aucuparia (SoAu, Rowan), and Betula pendula (BePe, Silver birch).
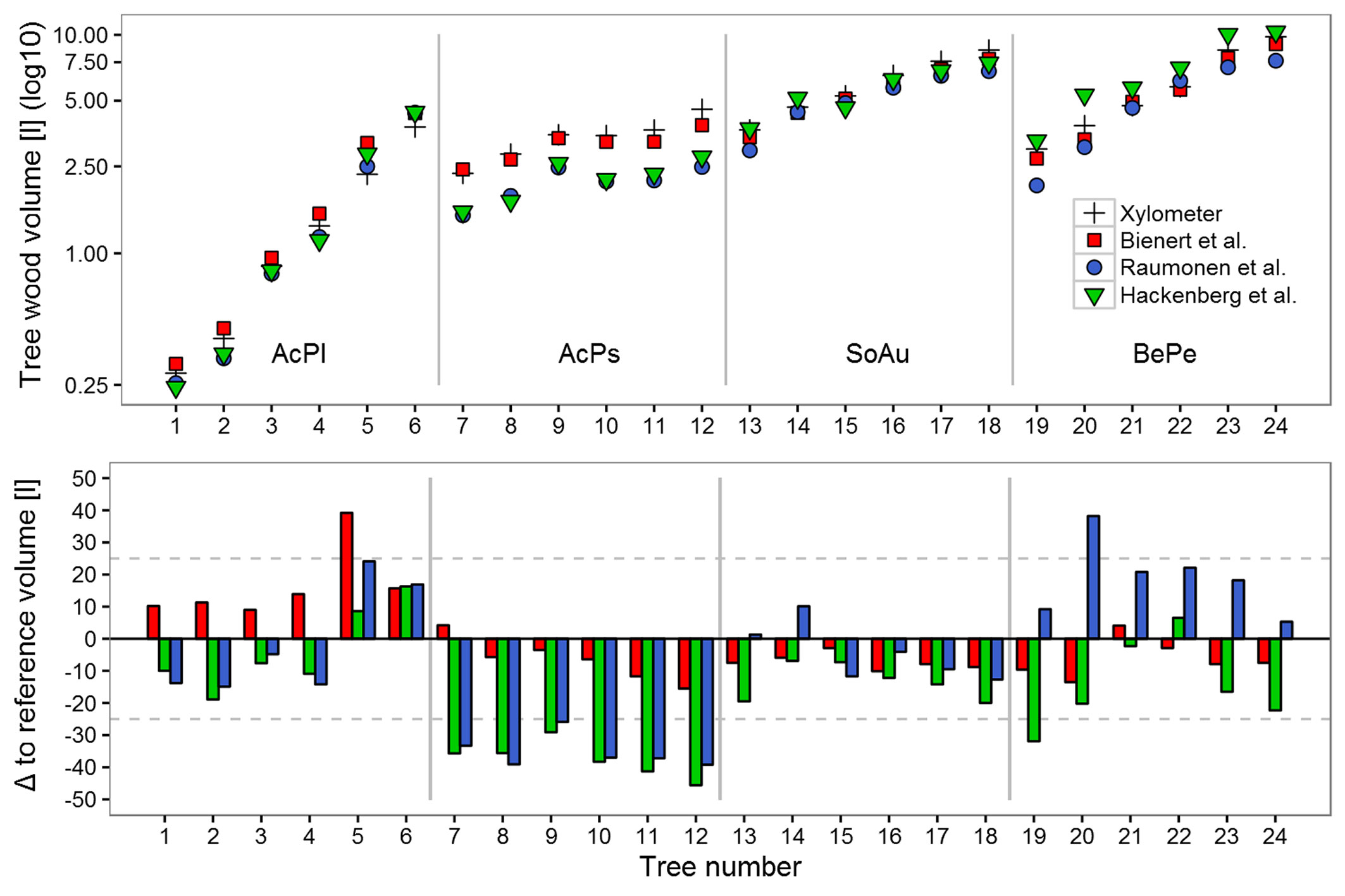
Tab. 1 - Characteristics of 24 trees of four species and wood volume estimates (in liter) from point clouds and reference volume from xylometric measurement (Xylo, in liter). Percentage difference for each method from reference volume is given in brackets. Trees are sorted by species and increasing diameter at breast height (DBH). Species abbreviations: (AcPl) Acer platanoides (Norway maple); (AcPs) Acer pseudoplatanus (Sycamore maple); (SoAu) Sorbus aucuparia (Rowan); (BePe) Betula pendula (Silver birch). (TH): Tree Height; (RMSE): Root Mean Square Error; (MAE): Mean Absolute Error.
| Species | No | Age (y) |
DBH (cm) |
TH (m) |
Xylo (l) |
Voxel-based (Bienert et al.) |
Cylinder-based (Raumonen et al.) |
Cylinder-based (Hackenberg et al.) |
|---|---|---|---|---|---|---|---|---|
| (l - Δ to Xylo) | ||||||||
| AcPl | 1 | 7 | 1.1 | 1.79 | 0.283 | 0.312 (+10.2%) | 0.244 (-13.8%) | 0.255 (-10.0%) |
| 2 | 7 | 1.4 | 2.23 | 0.408 | 0.454 (+11.3%) | 0.347 (-14.9%) | 0.331 (-18.9%) | |
| 3 | 7 | 1.8 | 3.12 | 0.875 | 0.954 (+9.0%) | 0.833 (-4.8%) | 0.808 (-7.6%) | |
| 4 | 7 | 2.0 | 4.88 | 1.335 | 1.520 (+13.9%) | 1.146 (-14.2%) | 1.189 (-10.9%) | |
| 5 | 7 | 2.8 | 4.75 | 2.300 | 3.201 (+39.2%) | 2.854 (+24.1%) | 2.499 (+8.6%) | |
| 6 | 7 | 4.1 | 3.98 | 3.789 | 4.384 (+15.7%) | 4.430 (+16.9%) | 4.408 (+16.3) | |
| AcPs | 7 | 16 | 2.5 | 5.52 | 2.324 | 2.422 (+4.2%) | 1.550 (-33.3%) | 1.494 (-35.7%) |
| 8 | 15 | 2.8 | 5.28 | 2.849 | 2.688 (-5.7%) | 1.734 (-39.1%) | 1.833 (-35.6%) | |
| 9 | 14 | 2.8 | 5.70 | 3.489 | 3.366 (-3.5%) | 2.586 (-25.9%) | 2.473 (-29.1%) | |
| 10 | 16 | 3.0 | 5.93 | 3.459 | 3.239 (-6.4%) | 2.180 (-37.0%) | 2.135 (-38.3%) | |
| 11 | 16 | 3.2 | 6.75 | 3.673 | 3.243 (-11.7%) | 2.308 (-37.2%) | 2.158 (-41.3%) | |
| 12 | 14 | 3.5 | 6.50 | 4.566 | 3.859 (-15.5%) | 2.768 (-39.2%) | 2.486 (-45.6%) | |
| SoAu | 13 | 11 | 2.9 | 7.02 | 3.675 | 3.398 (-7.5%) | 3.724 (+1.3%) | 2.960 (-19.5%) |
| 14 | 11 | 3.3 | 7.50 | 4.667 | 4.392 (-5.9%) | 5.138 (+10.1%) | 4.436 (-6.9%) | |
| 15 | 12 | 3.9 | 6.27 | 5.260 | 5.108 (-2.9%) | 4.644 (-11.7%) | 4.878 (-7.3%) | |
| 16 | 11 | 4.0 | 6.92 | 6.524 | 5.866 (-10.1%) | 6.256 (-4.1%) | 5.731 (-12.2%) | |
| 17 | 12 | 4.3 | 6.80 | 7.575 | 6.980 (-7.9%) | 6.858 (-9.5%) | 6.498 (-14.2%) | |
| 18 | 12 | 4.5 | 7.96 | 8.522 | 7.769 (-8.8%) | 7.442 (-12.7%) | 6.821 (-20.0%) | |
| BePe | 19 | 10 | 2.8 | 6.53 | 3.005 | 2.718 (-9.6%) | 3.280 (+9.2%) | 2.047 (-31.9%) |
| 20 | 10 | 3.1 | 6.76 | 3.841 | 3.322 (-13.5%) | 5.310 (+38.2%) | 3.064 (-20.2%) | |
| 21 | 10 | 3.5 | 5.76 | 4.742 | 4.938 (+4.1%) | 5.732 (+20.8%) | 4.633 (-2.3%) | |
| 22 | 10 | 3.6 | 6.68 | 5.787 | 5.618 (-2.9%) | 7.066 (+22.1%) | 6.165 (+6.5%) | |
| 23 | 10 | 4.5 | 7.35 | 8.513 | 7.839 (-7.9%) | 10.060 (+18.2%) | 7.107 (-16.5%) | |
| 24 | 10 | 4.6 | 6.99 | 9.801 | 9.067 (-7.5%) | 10.320 (+5.3%) | 7.618 (-22.3%) | |
| Sum (µ) | - | - | - | - | 101.262 | 96.657 (-0.8%) | 98.811 (-5.5%) | 83.936 (-17.3%) |
| RMSE | - | - | - | - | - | 0.453 (12.1%) | 0.913 (22.7%) | 1.030 (23.4%) |
| MAE | - | - | - | - | - | 0.369 (9.8%) | 0.752 (19.3%) | 0.818 (19.9%) |
We only used data for which comparable information was available and that was acquired in a controlled experimental setting. Although additional TLS-based point cloud data of trees is available online, including larger trees, these data sets are not always sampled with identical methods, e.g., in terms of reference measurements which are partly based on dry weight and not on xylometry analyses. Furthermore, in many cases data on branching structure or species information is missing. Hence, we focused on the analysis of a smaller but comprehensible data set of young trees.
Scan data acquisition, registration and post-processing
Trees were scanned under leaf-off conditions in May and December 2013, respectively ([5], [25]). In order to provide full coverage, all trees were scanned from four different positions, perpendicular to each other, using a FARO Photon 120® laser scanner (Korntal-Münchingen, Germany), with an angular step size 0.036° (2.5 mm point spacing at 4 m distance). The distance from each scan position to the trees was between 3-4 m. The instrument height was 130 cm. All scans were performed under clear skies and nearly windless conditions. Four polystyrene spheres (14.5 cm diameter) were used as reference targets for co-registration. The resulting point clouds contained 10.000-200.000 points, depending on the size and complexity of each tree. During the scan process, the built-in FARO LS Clear-Sky and Clear-Contour filters were applied to the captured data. These filters removed incorrect measurements (i.e., when a laser beam was reflected twice), and incorrect sky points. The individual scans for each tree were automatically registered into a local coordinate system with the FARO Scene® software version 5.0.1 ([16]) using the reference spheres. An overall registration accuracy of <3 mm was achieved for the point clouds. Individual trees were extracted manually from the registered point clouds using the software CloudCompare® version 2.54 ([15]). The point clouds of each tree were post-processed by a statistical outlier remover filter plugin (qPCL) within CloudCompare to remove residual noise and ghost points. The tree point clouds in our study do not show heavy shadowing effects as they were scanned from multiple sides under leaf-off conditions. For more details on the scanning and point cloud processing refer to Bienert et al. ([5]) and Hess et al. ([25]).
Volume estimation
Reference wood volume measurements
For the xylometric reference measurements all trunks were cut into segments of 65 cm length. Each trunk segment or branch bundle was then fully submerged in a specifically constructed cylindrical water container. The displaced and collected water was weighted and the equivalent water volume was calculated and assigned to each object. The xylometric volumes were determined directly after the scan process so that no reduction in wood volume is expected. The period of submergence of each tree part was short so that the impact of water permeation into the wood was negligible.
Wood volume estimation via voxel space analysis
For the voxel-based analysis we used the method of Bienert et al. ([5] - updated by [25], hereafter referred to as Bienert et al.). In a first step, a 3-D voxel space is generated based on the defined voxel size and the dimensions of the input point cloud. In a second step each point of the input cloud is assigned into a voxel based on its location. To remove outliers, e.g., single stray or noise points, a user-defined threshold can be set for the minimum number of points that a voxel must contain in order to be accepted. Here we used a consistent voxel size of 7 mm and a minimum number of two points per voxel. Smaller (5 mm) and larger (10 mm) voxel sizes were tested but did not improve the overall estimates. Ideally the chosen voxel size is set to be smaller than the largest stem diameter. If voxel grid downsampling is used, that is, to reduce the number of points of a point cloud to a certain resolution, the voxel size of the volume method is bounded by the chosen voxel grid resolution. To avoid overestimation, which can occur if the voxel size is too large, the voxel volume is adjusted to the point distribution in the X- and Y-voxel space using axis-parallel bounding boxes ([5]). For this adjustment the minimum number of two points within a voxel is sensible. After the voxelisation and bounding-box adjustment the algorithm identifies the occluded voxels (i.e., inner and shadowed parts of the stem and branches) by performing a local neighborhood analysis in the X- and Y-direction in the horizontal layer of each occupied voxel. Using counters occluded voxels are identified and added as tree voxels accordingly. This step is crucial because the volume estimate will be biased when these parts are not accounted for as volume ([18], [26]). In a final step the bounding boxes are expanded to the side-faces of their respective neighboring voxels and the volume is calculated by summing up the volumes of all bounding-box adjusted voxels. Here we worked with the original resolution of the point clouds.
Wood volume estimation via cylinder-model approaches
We used two geometric-primitive-based approaches to estimate wood volumes. The first approach we tested is the one originally developed by Raumonen et al. ([42] - hereafter referred to as Raumonen et al.) and which was further developed and validated in Calders et al. ([9]) and Raumonen et al. ([43]). The method partitions the point cloud into small subsets based on user-defined sizes. These subsets, or surface patches, work as the smallest units, which are used to segment the point cloud of a tree into the stem and individual branches. The segmentation is based on surface growing of the patches, starting from the base of the stem and branches, and locally checking connectivity of small group of patches. The partition into patches and the segmentation are performed twice: the first partition uses large uniformly sized patches to quickly estimate the branching structure and local branch size, and based on that the second partition uses patches of a smaller and variable size to produce finer segmentation. In the next step circular cylinders are fitted into the segments. The relative length (length/ radius) of the fitted cylinders approximately equals a user given value. It is also possible to fit other geometric primitives into the subsets, e.g., cones or elliptical cylinders. However, circular cylinders are the most robust primitive to describe the tree and its structure ([2]). Non-connecting cylinders are automatically extended to form a complete model. Finally the tree parameters of interest (i.e., wood volume, branch angles, branch and trunk diameter, etc.) can be read from the cylinder model. Because the partitions into patches are random, every modeling run produces slightly different models and therefore we always made five models per input and calculated the average from these models. The important input parameters were optimized for each tree by the following simple procedure: the models were calculated with all possible parameter combinations - the minimum patch size, the maximum patch size, relative cylinder length, and outlier removal radius for cylinder fitting - and the combination that was selected was the one with the smallest standard deviation of the point-to-model distances. The point-to-model distance (that is, the minimum of all the distances between the point and all cylinders) for automatic parameter optimization in the QSM building method relies on Hackenberg et al. ([22]). We used the following possible parameter values: minimum patch size of 5 mm and 10 mm; maximum patch size: 30 mm, 40 mm, 50 mm; relative cylinder length: 4, 6, 8; relative radius for outlier removal: 2, 2.5, 3, 3.5, 4. The algorithm runs in Matlab® (MathWorks, Natick, MA, USA) version R2015a.
The second approach we tested is by Hackenberg et al. ([20] - hereafter abbreviated as Hackenberg et al.). This approach utilizes search spheres to follow the tree’s branching structure from its root to its tips. On each sphere’s surface the cross sectional areas of the underlying branch are represented by circular point structures. Circles are fitted and then transformed to enlarged spheres. The method is repeated recursively with the new detected spheres and stops when a sphere reaches a tip or a large occlusion gap. An open source software exists ([21], [44]) with support given as a web page (⇒ http://www.simpletree.uni-frei burg.de). User and self-critics of the software’s author include the support for Linux OS only and a high-dimensional space of input parameters. A free plugin for the Computree platform (⇒ http://computree.onf .fr/?lang=en) was released accounting to both critics. The main operating system of Computree is Microsoft Windows® and the method parameters are guessed internally by point cloud and tree features and are optimized user-hidden. The sphere-following method is extended with the attractor technique presented in Côté et al. ([10], [11]) to allow the method to handle large gaps in the point clouds. The plugin is currently in an early alpha version, but could produce the results presented here, as well as on other available clouds. The full plugin will be presented in detail in a future publication as soon as it reaches a stable state. All 24 trees could be modelled in a total of 163 seconds (Intel(R) Xeon(R) CPU E5-1650 v3).
Statistical data analysis of the volumetric results was performed with R ([41]).
Results
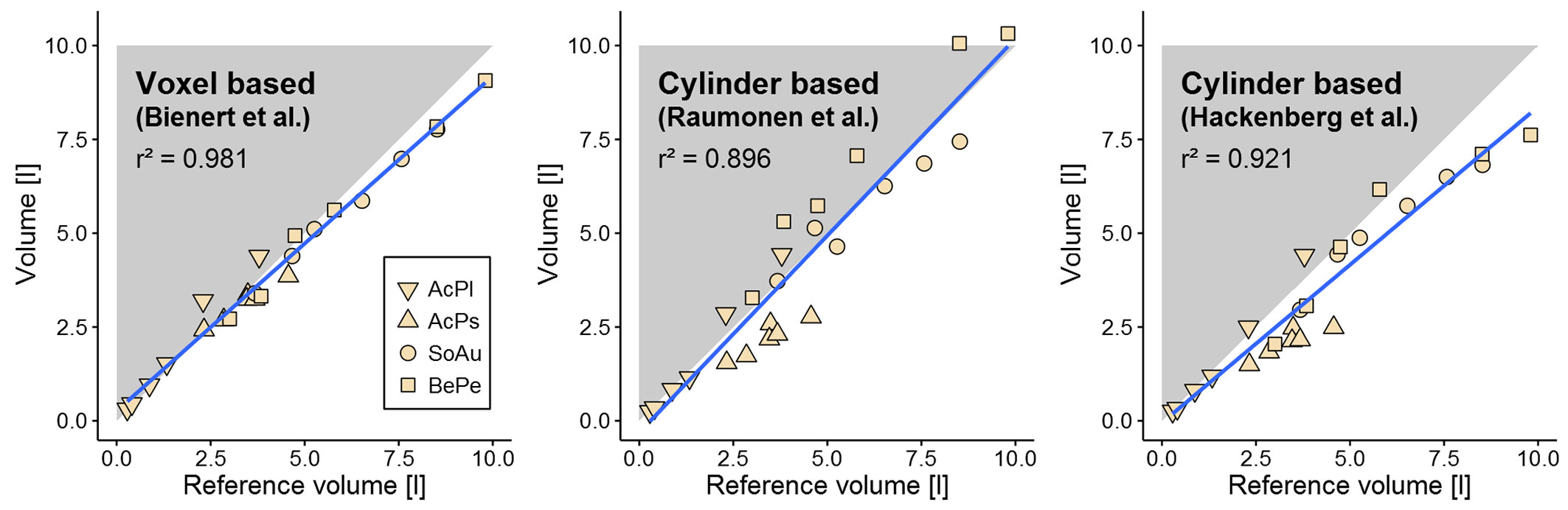
Wood volume estimates from the point clouds were successfully derived for all 24 trees with all three methods (Tab. 1). In general, all the three methods agreed well when compared to the xylometric reference measurements (Fig. 2). The voxel-based method gave the best results overall (r2 = 0.98 - Fig. 2) with an average underestimation of less than 1% (MAE 9.8%). The cylinder-primitive based method of Raumonen et al. showed a similar level of accuracy, with an underestimation of less than 6%, but showed a higher variance (MAE 19.3%, r2 = 0.90). The method of Hackenberg et al. performed less well because it tends to underestimate the volumes by 17.3% (MAE 19.9%, r2 = 0.92). When comparing the absolute volume (sum) of all trees the method by Raumonen et al. was closest to the reference measurements (Tab. 1).
Fig. 2 - Regression plots and r2 values between xylometric reference measurements and point cloud method based estimates. Methods: (left) Bienert et al. ([5]); (middle) Raumonen et al. ([42]); (right) Hackenberg et al. ([20]). Blue line shows linear fit between reference measurements and estimate. The 1:1 line is visualized by the diagonal borderline of the gray triangle. Different tree species are indicated by different point types. Species abbreviations: (AcPl) Acer platanoides; (AcPs) Acer pseudoplatanus; (SoAu) Sorbus aucuparia; (BePe) Betula pendula.
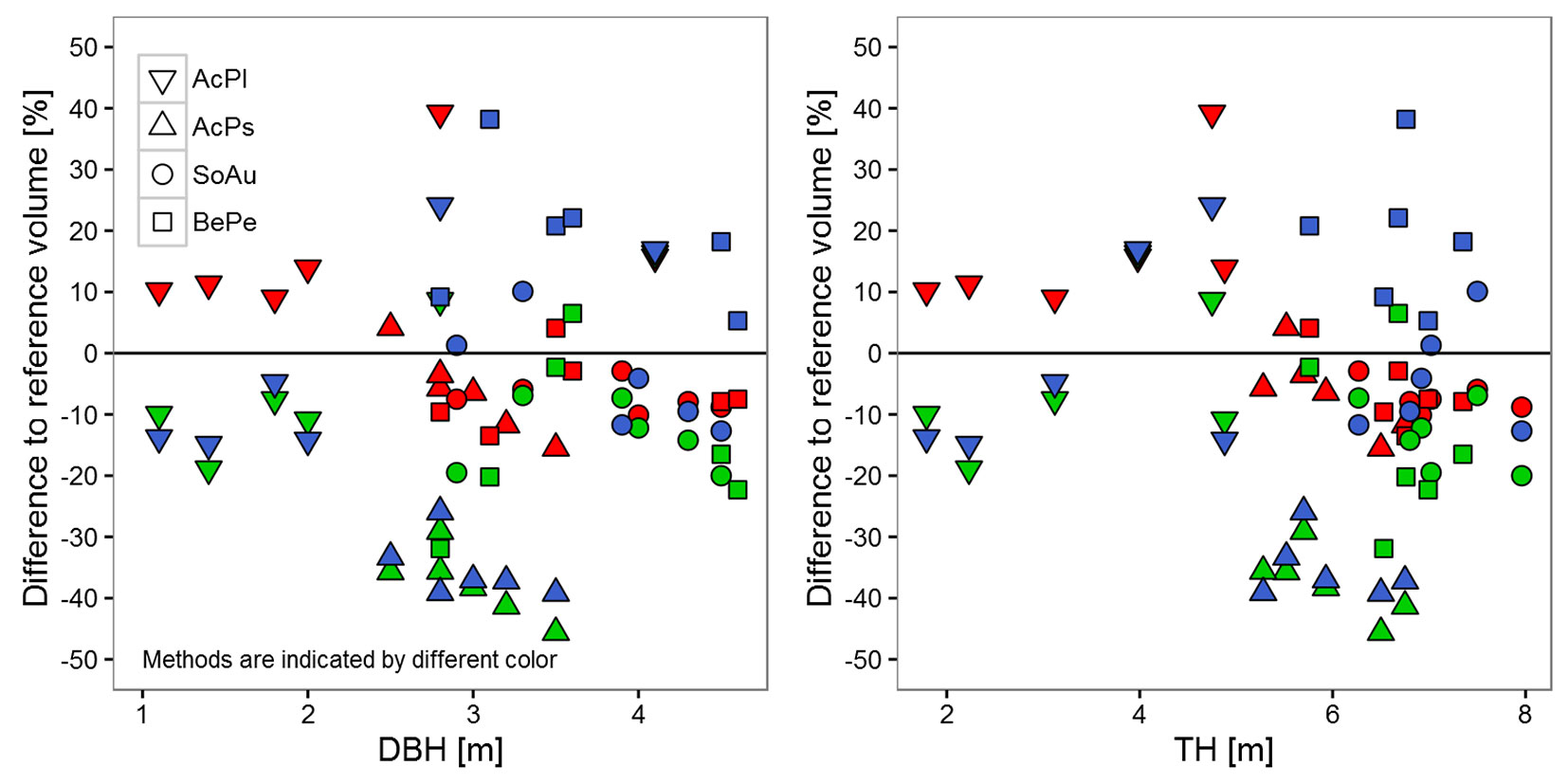
We found a significant variation in the error of the estimates between tree species across all methods (Tab. 2). The highest mean error over all three methods was obtained for an Acer pseudoplatanus tree (No. 12 in Tab. 1). The wood volume of this tree species was generally underestimated by all methods. The volumes derived for Betula pendula (species with a complex structure in our study) showed the strongest variations across methods. The estimates obtained for Sorbus aucuparia best agreed with the reference measurements and showed the lowest variations (Fig. 3). Comparing DBH and TH with the differences of the reference volumes did not reveal significant trends for the cylinder-based methods (Fig. 4). Only using the voxel-based method DBH (F1.22 = 18.4, p < 0.001) and TH (F1.22 = 5.3, p < 0.05) had a significant effect on the error of the estimates.
Tab. 2 - Effect of diameter at breast height (DBH), tree height (TH) and tree species on the error of the volume estimates using different methods. Significance of DBH and TH was tested using simple linear regression. Significance of tree species was tested by one-way ANOVA. (*): p<0.05; (**): p<0.01; (***): p<0.001; (ns): not significant.
| Parameter | Effect of error on volumetric estimate | ||
|---|---|---|---|
| Bienert et al. | Raumonen et al. | Hackenberg et al. | |
| DBH | * (F1.22=5.3) | ns | ns |
| TH | *** (F1.22=18.5) | ns | ns |
| Species | *** (F3.20=14.7) | *** (F3.20=22.5) | *** (F3.20=11.0) |
Fig. 3 - (Top): Wood volume estimates for 24 trees of four tree species from three different methods. Different methods are indicated by different point types and colors. Tree volumes are plotted on a logarithmic scale for easier comparison between small and larger volumes. Trees are sorted by species and increasing diameter at breast height (DBH). Species abbreviations: (AcPl) Acer platanoides; (AcPs) Acer pseudoplatanus; (SoAu) Sorbus aucuparia; (BePe) Betula pendula. (Bottom): Percentage difference of point cloud estimates to xylometric reference volume. ±25% value is plotted as dashed line for better visual interpretation. Vertical gray lines are plotted to differentiate between sets of different species.
Fig. 4 - Plot of diameter at breast height (DBH) and tree height (TH) versus the observed differences of all three methods to the reference volumes. Different tree species are indicated by different point types. Methods are indicated by color: red refers to Bienert et al. ([5]), blue refers to Raumonen et al. ([42]), green refers to Hackenberg et al. ([20]). Species abbreviations: (AcPl) Acer platanoides; (AcPs) Acer pseudoplatanus; (SoAu) Sorbus aucuparia; (BePe) Betula pendula.
Discussion
All three methods can be used to compute wood volume estimates for young trees from TLS-derived point clouds. The achievable accuracies are sufficiently high to grant reliable results in wide range of ecological and forestry applications. Currently, all the three tested methods rely on user input. In particular the two QSM methods require to set multiple parameters that can have a significant effect on the estimate, e.g., minimum radii. The complex setting of these parameters should be simplified to allow for the use of these methods without the need for advanced knowledge in point cloud modeling. For a better comparison of the tested methods we used identical parameter settings (see above) in each method for all trees in the sample.
The observed errors in the estimates can be mainly related to structural differences among tree species rather than to the methods themselves. Indeed, tree trunks hold most of the wood volume and can be extracted with high accuracies, while errors in volume estimation were mainly attributed to the branches ([22], [25]). Whereas branches are detected generally well, visual inspection of the resulting cylinder models using QSM methods showed that the observed underestimation, as well as overestimation, of the cylinder-primitive approaches was mainly explained by over- or under-sized cylinder diameters at thin branches. The bounding-box adjustment of the tested voxel-based method did not have this problem and showed the lowest overall error. For instance, Betula pendula typically consists of a large number of long thin branches, while Sorbus aucuparia is characterized by fewer, shorter and thicker branches. The latter species is less prone to error (see Tab. 2 and Fig. 3) due to a larger number of laser points that actually hit the branches (depending on the scan resolution) and a lower number of branches that may have an incorrect cylinder fit.
In few cases branches of higher order showed a larger cylinder diameter than branches of lower order. Actually, for most tree individuals this will not be true. Both cylinder-based methods use a threshold for the minimum size of cylinder radii at branches (2.5 mm in our case). If radii are smaller than this value they are adjusted (enlarged) to this threshold, leading to an overestimation especially at very thin branches. The methods of Raumonen et al. and Hackenberg et al. gave similar results except for Betula pendula. The large number of branches in this species, especially second order branches, yielded a larger overall error even though the error of the fitted cylinder radii can be small. Contrastingly, the large underestimation observed for Acer pseudoplatanus (36% on average) using the cylinder-based methods could not be related to any specific tree parameter. A possible explanation could be that the trunk and branches are not of cylindrical shape or that the ratio between cylinder length and radius is not suited for the samples of this tree species. However, for Sorbus aucuparia we did not observe such a large underestimation, despite its higher structural complexity. Another possibility are registration errors or noise in the point clouds.
The fact that the tree species had a significant influence on the error of the estimate using all methods (Tab. 2) calls for sets of species-specific parameters, especially for the cylinder-based methods. Currently such parameter sets do not exist and more research for a range of tree species is required. In the practice, it will not always be possible to know the species of a tree that is represented in the point cloud; however, even in such cases species-specific parameter sets would be useful. By analyzing the QSM information for a set of reference species, groups of parameters that describe that species, e.g., using support vector machines or linear discriminant analysis, may be developed (see Tab. 3). This would help identifying the species identity for trees of unknown species in the point cloud in large scale studies on natural forests. In particular, parameters accounting for the structural characteristics of a species or a group of species are desirable. One suggestion is to set the minimum branch diameters based on the branch order level and the type of species. To this purpose, iterative approaches could be applied which optimize the method parameters and identify the species first, before applying this information in consecutive runs.
Tab. 3 - Potential group of structural tree (species) parameters for the description and development of species specific parameters settings of point-cloud based methods for wood volume estimation. Diameter at breast height (DBH), tree height (TH), ground diameter (GD).
| Tree (species) parameters |
|---|
| Height, DBH (or GD) Height/DBH (or GD) ratio |
| Number of branches |
| Minimum branch radius |
| Mean branch length/radius ratio |
| Mean branch angle |
| Maximum branch order |
| Stem/branch radius ratio |
The observed influence of DBH and TH on the error using the voxel-based method (Tab. 2, Fig. 4) indicates that it is not feasible to apply a constant voxel size for all point clouds in the case of large variations in DBH and branch diameter. In our case a voxel size of 7 mm was suitable for all tree samples (young understorey trees, TH < 8 m), but this may not fit when analyzing larger trees and sample sizes. When the wood volume at the plot level is required and larger trees are included in the sample, this has to be considered and carefully adapted. In this regard, cylinder-based methods adapt much better to variations in diameters and tree height, though they yield larger errors of the estimates. The voxel-based method of Bienert et al. ([5]) currently does not calculate the branching structure. To improve that method a tree-skeletonization routine could be included to allow for local adjustments of the voxel size, together with the bounding-box adjustment routine, at branches of higher order. An initial voxel size estimate based on DBH and TH should be used to set the optimal voxel size. DBH and TH can be extracted relatively straight forward ([12]) and ground truth sampling is not required.
Conclusions
All three methods compared in this study proved to be appropriate (in terms of their accuracy) to derive wood volumes of young deciduous trees from TLS point clouds. This is promising for their use in wider ecological applications such as tree-growth analysis ([49]) or long-term forest biodiversity experiments were non-destructive measurements are essential ([29]). The use of voxel-based methods should be favored when only the total tree volume has to be estimated, as these methods are easy to use and yield robust results. However, the geometric-primitive (QSM) based approaches currently offer more output parameters (e.g., branching order, branch angles and radii) in a very small file size. This additional information is highly valuable in terms of finding optimized method parameters that account for species-specific differences in the structural complexity and branch sizes. Currently, such parameter sets do not exist and further research with a larger sample is required. Although all the three tested methods include some optimization or adjustment routines, their initial input parameters were not altered with regards to the tree species - which is highly related to the error of the estimate. Therefore, careful consideration is needed to select the best input parameters for each method, as initial information on the trees and their respective point clouds is essential. Using species-specific parameter sets and combining the advantages of voxel-based and cylinder-based methods the estimation of highly accurate wood volume estimates from point clouds of trees is certainly possible.
Advancements of the methods analyzed in this study can also help to provide improved estimates of the related tree biomass, which is the goal of many studies. Allometric regression models including TLS-based information can be provided with more accurate information compared to simple point cloud metrics ([47]). Nonetheless, wood densities are currently still required to convert the volumes into an accurate estimate of biomass.
Acknowledgements
MK performed the data analysis and wrote the manuscript. CH and GvO conceived and designed the field experiments. CH carried out the field work. CH, PR, AB, JH and AF analysed the data and contributed to the manuscript. HGM, WH, AF and GvO contributed to the interpretation of the results and preparation of the manuscript.
We thank Moritz-Christian von Oheimb for support in obtaining the experimental data from Enzen forest. Carsten Hess is very grateful to the program and scholarship of the Leuphana Graduate School “DIABOLO - Distributed, Integrated and Harmonised Forest Information for Bioeconomy Outlooks”. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the grant agreement no. 633464.
References
CrossRef | Gscholar
Online | Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Goddert Von Oheimb
Institute of General Ecology and Environmental Protection, Technische Universität Dresden, PF 1117, 01735 Tharandt (Germany)
Werner Härdtle
Andreas Fichtner
Faculty of Sustainability, Institute of Ecology, Leuphana University Lüneburg, Scharnhorststr. 1, Lüneburg 21335 (Germany)
Department of Mathematics, Tampere University of Technology, PO Box 553, 33101 Tampere (Finland)
Hans-Gerd Maas
Institute of Photogrammetry and Remote Sensing, Technische Universität Dresden, 01062 Dresden (Germany)
INRA, Centre de Nancy, Biogéochimie des Ecosystèmes Forestiers, Champenoux (France)
Corresponding author
Paper Info
Citation
Kunz M, Hess C, Raumonen P, Bienert A, Hackenberg J, Maas H-G, Härdtle W, Fichtner A, Von Oheimb G (2017). Comparison of wood volume estimates of young trees from terrestrial laser scan data. iForest 10: 451-458. - doi: 10.3832/ifor2151-010
Academic Editor
Luca Salvati
Paper history
Received: Jun 27, 2016
Accepted: Feb 16, 2017
First online: Apr 04, 2017
Publication Date: Apr 30, 2017
Publication Time: 1.57 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2017
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 43211
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 35832
Abstract Page Views: 2655
PDF Downloads: 3667
Citation/Reference Downloads: 49
XML Downloads: 1008
Web Metrics
Days since publication: 2576
Overall contacts: 43211
Avg. contacts per week: 117.42
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Feb 2023)
Total number of cites (since 2017): 19
Average cites per year: 2.71
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Review Papers
Remote sensing-supported vegetation parameters for regional climate models: a brief review
vol. 3, pp. 98-101 (online: 15 July 2010)
Review Papers
Remote sensing of selective logging in tropical forests: current state and future directions
vol. 13, pp. 286-300 (online: 10 July 2020)
Review Papers
Accuracy of determining specific parameters of the urban forest using remote sensing
vol. 12, pp. 498-510 (online: 02 December 2019)
Technical Reports
Detecting tree water deficit by very low altitude remote sensing
vol. 10, pp. 215-219 (online: 11 February 2017)
Technical Reports
Remote sensing of american maple in alluvial forests: a case study in an island complex of the Loire valley (France)
vol. 13, pp. 409-416 (online: 16 September 2020)
Research Articles
Assessing water quality by remote sensing in small lakes: the case study of Monticchio lakes in southern Italy
vol. 2, pp. 154-161 (online: 30 July 2009)
Research Articles
Modelling dasometric attributes of mixed and uneven-aged forests using Landsat-8 OLI spectral data in the Sierra Madre Occidental, Mexico
vol. 10, pp. 288-295 (online: 11 February 2017)
Research Articles
Estimating biomass of mixed and uneven-aged forests using spectral data and a hybrid model combining regression trees and linear models
vol. 9, pp. 226-234 (online: 21 September 2015)
Research Articles
Afforestation monitoring through automatic analysis of 36-years Landsat Best Available Composites
vol. 15, pp. 220-228 (online: 12 July 2022)
Research Articles
High resolution biomass mapping in tropical forests with LiDAR-derived Digital Models: Poás Volcano National Park (Costa Rica)
vol. 10, pp. 259-266 (online: 23 February 2017)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword