Earlywood vessel features in Quercus faginea: relationship between ring width and wood density at two sites in Portugal
iForest - Biogeosciences and Forestry, Volume 8, Issue 6, Pages 866-873 (2015)
doi: https://doi.org/10.3832/ifor1346-008
Published: Apr 27, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
Wood anatomy holds relevant information for tree development and timber quality (e.g., wood density), which is important for the sustainability of the species. Quercus faginea Lam. (Portuguese or Lusitanian oak) is an autochthonous Mediterranean oak species characterized by a shrinking natural distribution area and use abandonment. We studied the variation of several wood properties and their relationships with the aim of determining and possibly increasing the wood economic value of this species. The anatomical features of earlywood vessels (area, number, frequency and proportion) were investigated in twenty Q. faginea trees sampled at two locations within the natural distribution of the species in Portugal. Moreover, we analyzed the variation of vessel features from pith to bark, the radial growth and the wood density to search for patterns and relationships among the analyzed parameters. Mean earlywood vessel area increased with cambial age up to 60-70 years and then leveled off. An inverse pattern was found for the number of vessels per ring beyond that age. Similar radial patterns of all vessel features were found at both sites, and no significant differences in earlywood vessel area were found between sites. The within-tree development of earlywood vessels was age-related, though not influenced by growth. Earlywood vessel features explained the variation of wood density, i.e., wood density of Q. faginea was strongly negatively correlated with both mean vessel area and proportion.
Keywords
Quercus faginea, Earlywood Vessels, Wood Density, Ring Width, Variation
Introduction
Vessel size and distribution throughout a growth ring deeply affect tree physiology and wood utilization. Vessels are the main cell types of the vascular transport system of plants and their importance is higher when the species are under threat of, for example, drought. In fact, the conductive area of vessels seems related to the conductive efficiency and tracks intra-seasonal information ([7], [15], [16]). Wood characteristics such as texture (i.e., the wood appearance due to cell morphology and density) are affected by vessel characteristics, thereby the quality of wood products is also vessel related ([43], [39]).
The measurement of vessel features such as area and diameter used to be a very time-consuming task. However, the current use of microscopy coupled with image analysis makes data acquisition and processing more efficient ([18], [33], [14], [24]). Recently, the number of studies focusing on the variation of vessel features (e.g., with age, growth and site) and their relation to other wood characteristics (e.g., density) has increased, although data is still scanty and results are often species-specific. The main tendencies in studies on vessel diameter variation have been recently discussed by Anfodillo et al. ([3]), with special attention to the relationship between axial conduit widening and tree height.
Vessels are key contributors to wood density, that is inversely proportional to their size and number ([34]). In oaks, vessel proportion (i.e., the percentage of xylem cross-section occupied by vessels) is one of the major anatomical factors affecting latewood density ([31]) and specific gravity ([42]). For instance, in Quercus suber vessel size and number were found to contribute significantly to mean ring wood density ([25]).
Contrasting results have been reported so far regarding the variation of vessels with age and tree growth. In Quercus alba the percentage of earlywood vessel area was influenced by the radial position, but not by the ring width ([28]). Earlywood vessel area was larger in fast-growing than in slow-growing Juglans nigra trees, but no correlation was found between the earlywood vessel area and ring width ([28]). Denne et al. ([13]) reported that the total vessel proportion decreased significantly as the ring width increase in Nothofagus nervosa, a diffuse porous hardwood species. In Q. suber, the vessel size increased from pith outwards, explaining 32% of the total variation in wood ring density ([24], [25]). In Q. rubra, vessel percentage was also found to be correlated with specific gravity, independently of soil types ([20]). As for ring porous species, it is generally accepted that latewood width is responsible for the variation in wood ring density, while earlywood width is relatively constant ([9]).
Quercus faginea Lam. is a ring porous oak natural occurring mainly in Portugal and Spain. It was more abundant in the XV-XVI centuries when it was used as a valued timber species, while nowadays it is mostly considered for conservation purposes ([6], [8]). Recent studies have shown that vessels represent about 15-17 % of the xylem tissue in Q. faginea, with higher values near the bark, and earlywood vessel diameters also increased radially from pith to bark ([38]). In this species wood density components (ring-wood, earlywood and latewood density) decreased radially and were influenced by tree growth factors ([23]).
In this work, the distribution pattern of earlywood vessels within the ring and its relationship with the cambial age have been investigated, as well as the relation between vessel parameters and wood density components. To address the above goals, earlywood vessel features (area, number, frequency and proportion) were analyzed in relation to ring width and wood density in Q. faginea trees grown in two sites located in the natural range of the species in Portugal. Sampling included 10 trees with 40 years of age on average and 10 trees with a mean age of 125 years.
Material and methods
Twenty Q. faginea trees were selected in naturally-regenerated, unmanaged forests in Portugal, near Macedo de Cavaleiros (site 1 - 41° 30′ N, 7° 01′ W) and Vimeiro (site 2 - 39° 29′ N, 9° 01′ W). The climate is Mediterranean tempered by oceanic influence. The mean annual temperature is 12 and 15 °C, and the mean annual rainfall 700 and 890 mm at site 1 and 2, respectively. The mean summer precipitation (from June to August) is 61 and 70 mm at site 1 and 2, respectively. Meteorological data available for the most recent 30 years were collected at the meteo stations of Bragança (for site 1) and Vimeiro (for site 2). The soils are classified as orthic dystric and eutric leptosols at site 1 and chromic cambisols at site 2 ([1], [22]).
Ten dominant or co-dominant trees with no visible signs of decay were harvested at each site. Sampled trees were on average 40 and 125 years-old at the time of sampling in site 1 and 2, respectively. Mean diameter at 1.30 m above the ground was 21 and 37 cm, and mean tree height was 11 and 15 m at site 1 and 2, respectively. For each sampled tree, a wood disc was excised at 1.3 m above the ground level. The wood was analyzed within a radial strip from pith to bark taken in the same compass direction.
Wood density was determined by X-ray microdensitometry and the first results were reported in Knapic et al. ([23]). The data on mean ring density, earlywood density, latewood density, heterogeneity index, latewood percentage and ring width were comprehensively analyzed and related with vessel features. The transverse surface of the wood strips used for X-ray measurements was smoothed by fine sanding until pores (vessels) were clearly visible under low magnification. White wax was applied on the surface to fill the vessels, thus allowing a better distinction from the surrounding tissues. A light microscope (Leica DMLA) with 8× optical magnification (1 pixel = 0.00704 mm) was coupled with a digital camera (Leica CCD) to capture sequential images along the radial direction from the pith outwards, by using an image analysis software (Leica Q Win Plus). Images were then converted to grey pixels following the methodology proposed by Leal et al. ([24]). Count of earlywood vessels and measurement of their area were performed. After a preliminary analysis of size distribution of all vessels, the minimum area for vessel to be included in further analyses was set to 0.001 mm2, thus discarding smaller vessels. Earlywood was differentiated essentially by the line(s) of large vessels, in contrast to the small vessels region characterizing the latewood.
Mean vessel area (or lumen area of earlywood vessels), vessel proportion (percentage of cross sectional area occupied by the earlywood vessels per growth ring), vessel number (total of earlywood vessels counted by ring) and vessel frequency (number of earlywood vessels per mm2) were determined for each annual ring, totaling about 1650 rings. Measurements were carried out within a frame window of approximately 2.3 mm of tangential width, while the radial dimension varied with each earlywood width, from the inner to the outermost ring. For the determination of vessel frequency and proportion, the total window measurement frame area excluding rays was used.
Terminology follows the IAWA list of microscopic features for hardwood identification ([21]).
Statistical analysis were performed (α = 0.05) using the software package SPSS® ver. 19 (IBM, NY, USA) to analyze the cambial age (i.e., ring number), tree and site effects on earlywood vessel features (mean area, number, density and proportion). Pearson’s correlations among ring width and ring density components were determined, and regression curves estimated.
Results
Variation of earlywood vessel features
The ring porous nature of the Q. faginea wood was clear both in very narrow growth rings (e.g., at the outermost rings of the older trees) and within the inner growth rings (Fig. 1a, Fig. 1b). For a detailed description of the wood anatomy of the species, see Sousa et al. ([38]).
Fig. 1 - Macroscopic view of transverse sections of Quercus faginea wood. The inner (A) and outer (B) growth ring structure are showed. Vessels are fullfilled with white wax and labele. Bar scale = 2 mm.
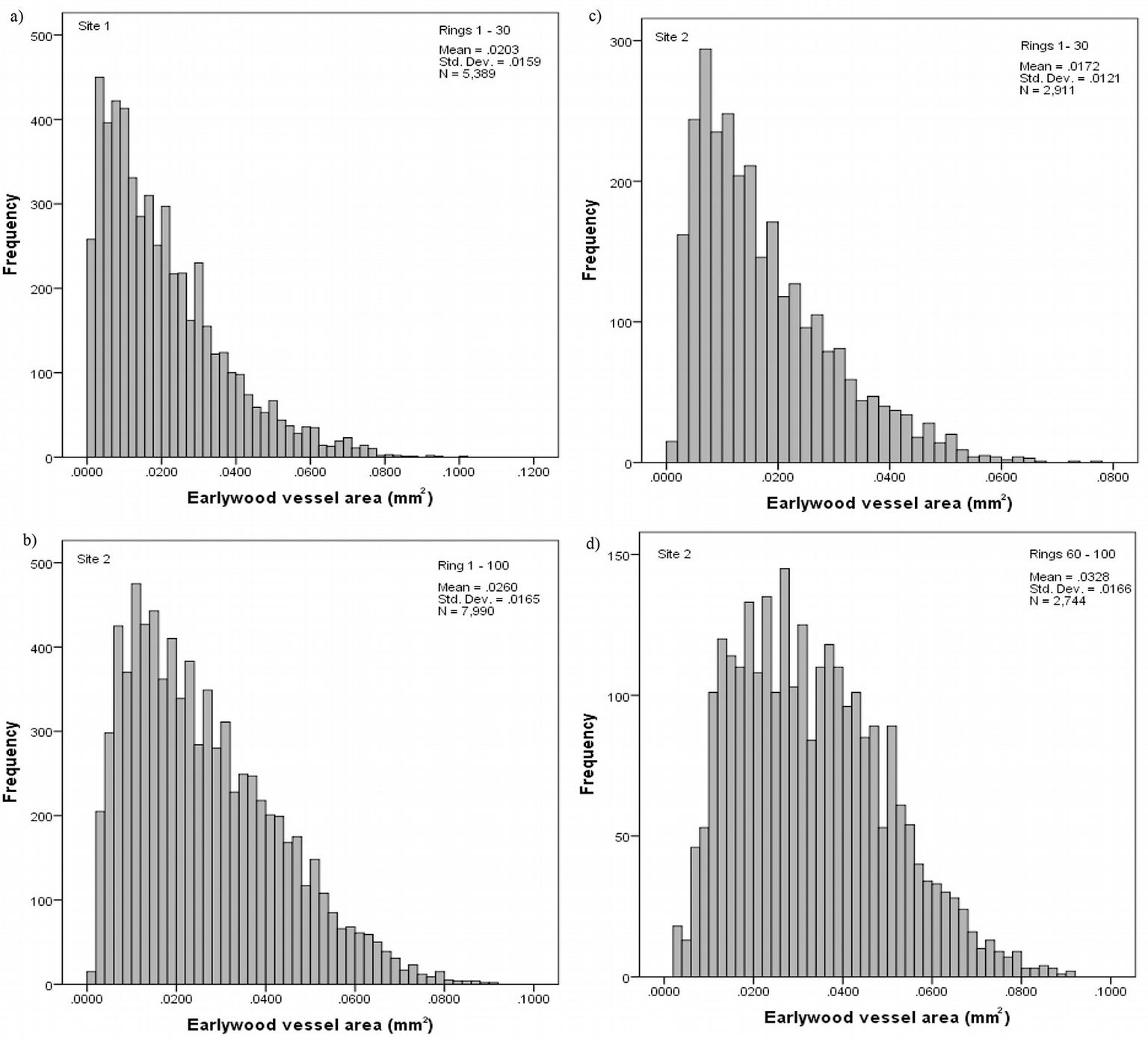
The frequency distribution of vessel area was skewed to the left at both sampling sites, even though more pronounced at site 1 (Fig. 2a, Fig. 2b). Analyzing the above distribution by age intervals, we observed that small vessels with area ≤ 0.020 mm2 are more frequent in the initial years, while above 60 years the distribution is no longer skewed (Fig. 2c, Fig. 2d).
Fig. 2 - Frequency distribution of the vessel area at site 1 (a) and site 2 (b), and by age intervals at site 2, from ring 1st to 30th (c) and from 60th to 100th (d).
Tab. 1 summarize the observed vessel features at each sampling site. Overall, mean vessel area, vessel frequency and vessel proportion were relatively higher at site 2 as compared with site 1, while vessel number was lower.
Tab. 1 - Mean value, coefficient of variation (in brackets) and range (lower row) of earlywood vessel area (MVA, mm2), vessel number (NV), vessel frequency (VF, n mm-2) and vessel proportion (VP, %) by tree at site 1 (mean of 30 rings by tree) and site 2 (mean of 100 rings by tree).
| Site | MVA | NV | VF | VP |
|---|---|---|---|---|
| 1 | 0.020 (78) 0.013-0.034 |
18.0 (59) 7.0-19.0 |
3.1 (52) 2.0-4.6 |
6.0 (67) 1.1-8.0 |
| 2 | 0.026 (78) 0.018-0.030 |
8.1 (45) 6.2-10.1 |
4.2 (77) 2.1-8.0 |
9.9 (74) 5.3-15.9 |
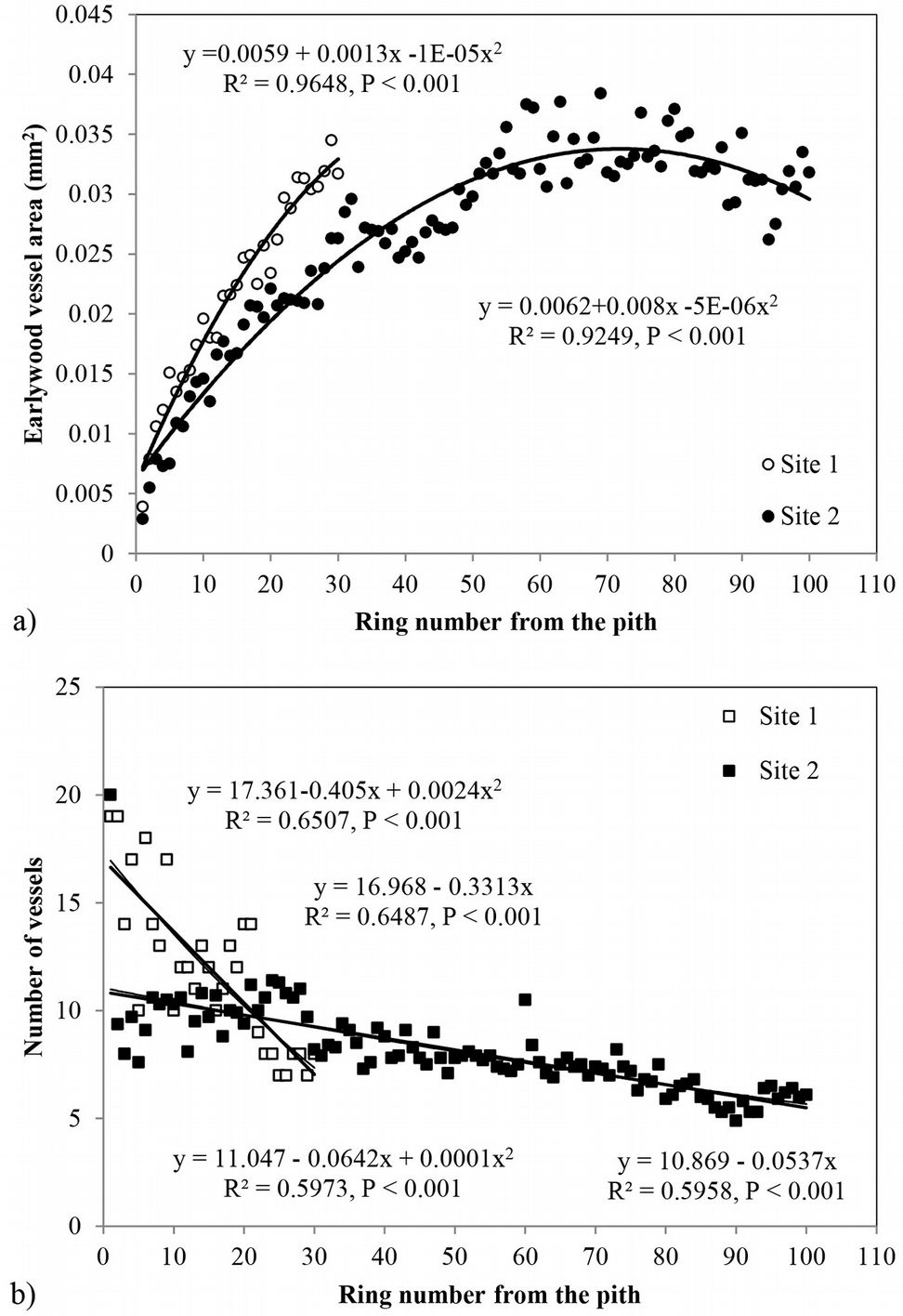
Radial variation of earlywood vessel area showed a large increase in the initial years up to the 60/70th rings, with a slight decrease onwards (Fig. 3a). At site 2 the maximum earlywood vessel area reached 0.038 mm2, decreasing to 0.032 mm2 (ca. 200 µm tangential diameter) near the bark. The increment of vessel area over the same cambial age period was higher at site 1. Regression analysis indicated that a second degree polynomial model best predicted the mean vessel area as a function of cambial age (R2=0.96, p < 0.001 and R2=0.92, p < 0.001 at site 1 and 2, respectively - Fig. 3a).
Fig. 3 - Radial variation of (a) mean earlywood vessel area and (b) number of vessels per growth ring in Quercus faginea wood at both sites. Each point represents the mean of 10 trees at each site.
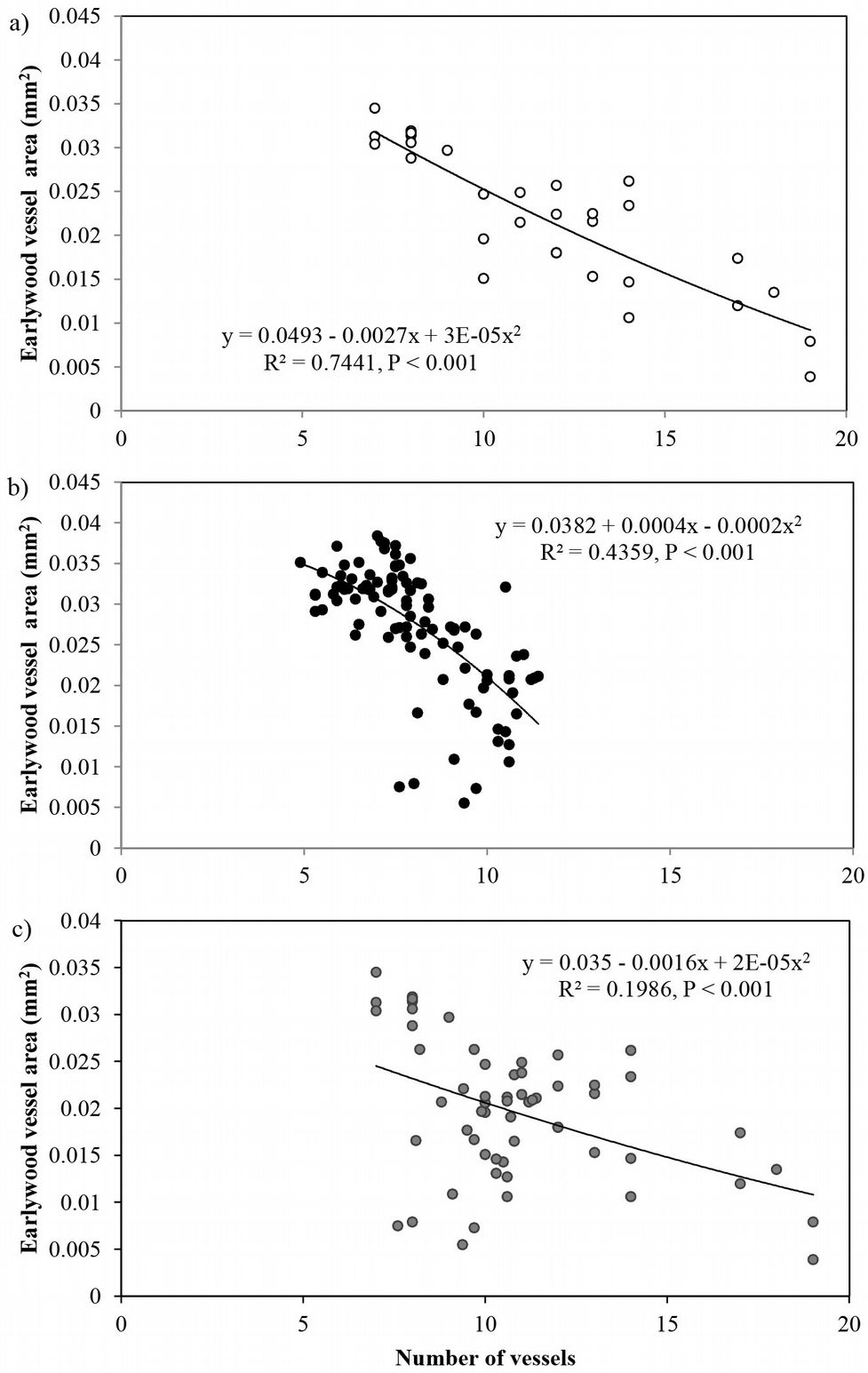
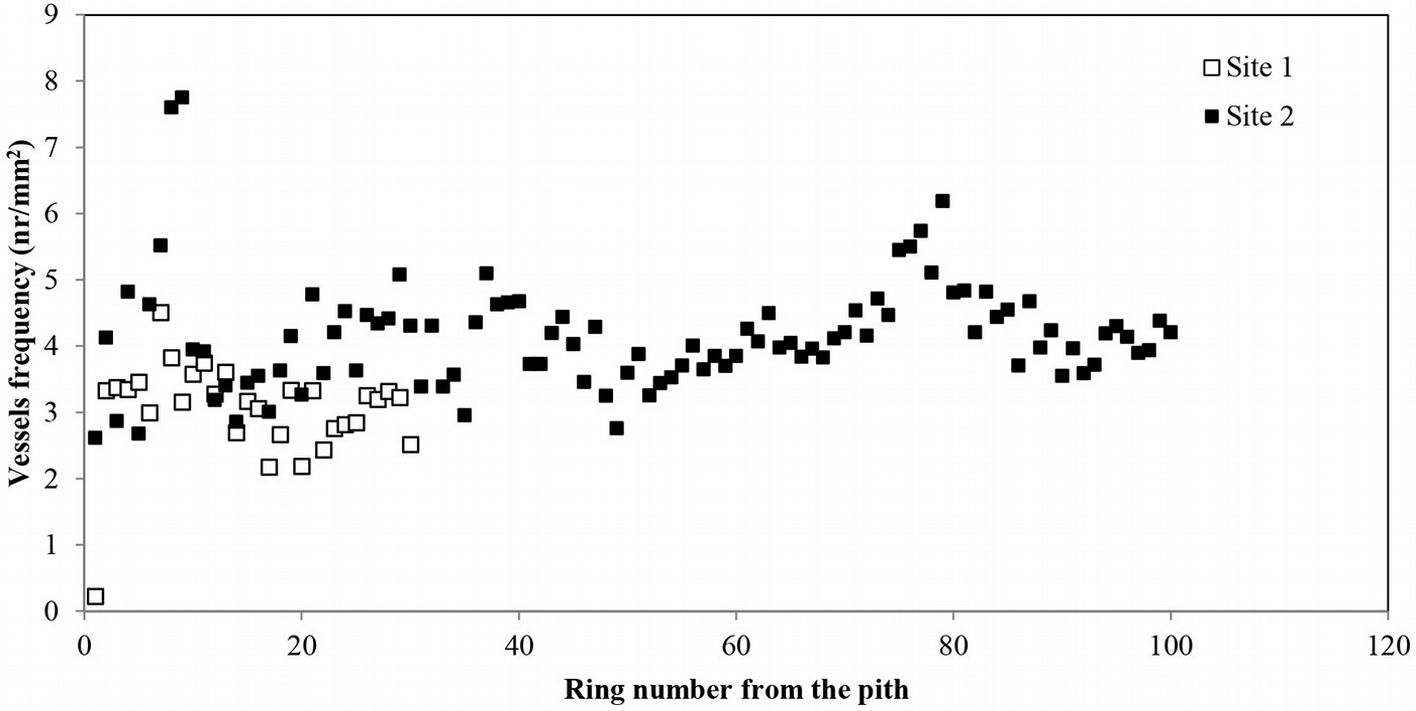
The average vessel number decreased at both sites from pith to bark, though the decrease was more pronounced at site 1 (Fig. 3b). For predicting vessel number based on cambial age, both second degree polynomial and linear regression proved to fit well (R2= 0.72, p <0.001 and R2= 0.60, p <0.001 at site 1 and 2, respectively). The relationship between the number of vessels and the mean vessel area per ring fitted both linear and second degree polynomial curves well (R2=0.74, p <0.001) at site 1 (Fig. 4a), while a poorer fitting (though still significant at p<0.001) was observed analyzing both sites and site 2 separately (Fig. 4b, Fig. 4c). Indeed, medium to strong negative correlations were found between the number of vessels and mean vessel area (Pearson’s r = -0.162 at both sites; r = -0.461 at site 1; r = -0.216 at site 2 - Tab. 2, Tab. 3, Tab. 4). Although some year-to-year fluctuations occurred, no specific trends of variation of vessel frequency with age was observed (Fig. 5).
Fig. 4 - Relationship between the number of earlywood vessels and the mean earlywood vessel area in Quercus faginea wood at: (a) site 1, within the first 30 rings; (b) site 2 ,within the first 100 rings; and (c) both sites, within the first 30 rings. Each point represents the mean value of 10 trees at each site.
Tab. 2 - Correlation coefficients between vessel variables, wood density and ring width within the first 30 rings at site 1. (NV): number of vessels; (MVA): mean vessel area; (VD): vessel density per ring width; (VP): vessel proportion per ring width; (MD): mean wood density; (EWD): earlywood density; (LWD): latewood density; (LWP): latewood proportion; (RW): ring width. (**): p<0.01 (2-tailed). Mean values by tree and ring (n=300, 30 rings × 10 trees).
| Variable | NV | MVA | VD | VP | MD | EWD | LWD | LWP | RW |
|---|---|---|---|---|---|---|---|---|---|
| NV | 1 | -0.461** | 0.357** | -0.233** | 0.157** | 0.071 | 0.16** | 0.119 | 0.486** |
| MVA | - | 1 | -0.21** | 0.627** | -0.419** | -0.395** | -0.36** | -0.229** | -0.225** |
| VD | - | - | 1 | 0.315** | -0.064 | 0.053 | -0.03 | -0.322** | -0.411** |
| VP | - | - | - | 1 | -0.455** | -0.399** | -0.39** | -0.304** | -0.477** |
| MD | - | - | - | - | 1 | 0.858** | 0.975** | 0.251** | 0.194** |
| EWD | - | - | - | - | - | 1 | 0.791** | -0.1 | 0.04 |
| LWD | - | - | - | - | - | - | 1 | 0.178** | 0.166** |
| LWP | - | - | - | - | - | - | - | 1 | 0.377** |
| RW | - | - | - | - | - | - | - | - | 1 |
Tab. 3 - Correlation coefficients between vessel variables, wood density and ring width within the first 100 rings common to all trees at site 2. Mean values by tree and ring (n=898, 100 rings × 10 trees excluding rings without vessels). (**): p<0.01 (2-tailed). Labels as in Tab. 2.
| Variable | NV | MVA | VD | VP | MD | EWD | LWD | LWP | RW |
|---|---|---|---|---|---|---|---|---|---|
| NV | 1 | -0.216** | 0.154** | -0.023 | 0.204** | 0.123** | 0.244** | 0.071 | 0.462** |
| MVA | - | 1 | -0.086** | 0.489** | -0.322** | -0.337** | -0.287** | 0.004 | -0.174** |
| VD | - | - | 1 | 0.579** | -0.211** | -0.135** | -0.229** | -0.172** | -0.391** |
| VP | - | - | - | 1 | -0.374** | -0.254** | -0.383** | -0.265** | -0.557** |
| MD | - | - | - | - | 1 | 0.909** | 0.975** | 0.217** | 0.385** |
| EWD | - | - | - | - | - | 1 | 0.841** | -0.022 | 0.19** |
| LWD | - | - | - | - | - | - | 1 | 0.179** | 0.424** |
| LWP | - | - | - | - | - | - | - | 1 | 0.352** |
| RW | - | - | - | - | - | - | - | - | 1 |
Tab. 4 - Correlation coefficients between vessel variables, wood density and ring width within the common years period (the first 30 rings) at both sites. Mean values by tree and ring (n=589, 30 rings × 20 trees excluding rings without vessels). (**): p<0.01 (2-tailed). Labels as in Tab. 2.
| Variable | NV | MVA | VD | VP | MD | EWD | LWD | LWP | RW |
|---|---|---|---|---|---|---|---|---|---|
| NV | 1 | -0.162** | 0.075 | -0.07 | -0.166** | -0.228** | -0.147** | 0.164** | 0.541** |
| MVA | - | 1 | -0.16** | 0.519** | -0.449** | -0.449** | -0.401** | -0.013 | -0.003 |
| VD | - | - | 1 | 0.462** | -0.063 | 0.008 | -0.084 | -0.15** | -0.331** |
| VP | - | - | - | 1 | -0.367** | -0.277** | -0.352** | -0.228** | -0.425** |
| MD | - | - | - | - | 1 | 0.895** | 0.978** | 0.044 | -0.074 |
| EWD | - | - | - | - | - | 1 | 0.842** | -0.242** | -0.221** |
| LWD | - | - | - | - | - | - | 1 | 0.003 | -0.061 |
| LWP | - | - | - | - | - | - | - | 1 | 0.377** |
| RW | - | - | - | - | - | - | - | - | 1 |
Fig. 5 - Radial profile of earlywood vessel frequency per growth ring in Quercus faginea wood. Each point represents the mean of 10 trees at each site.
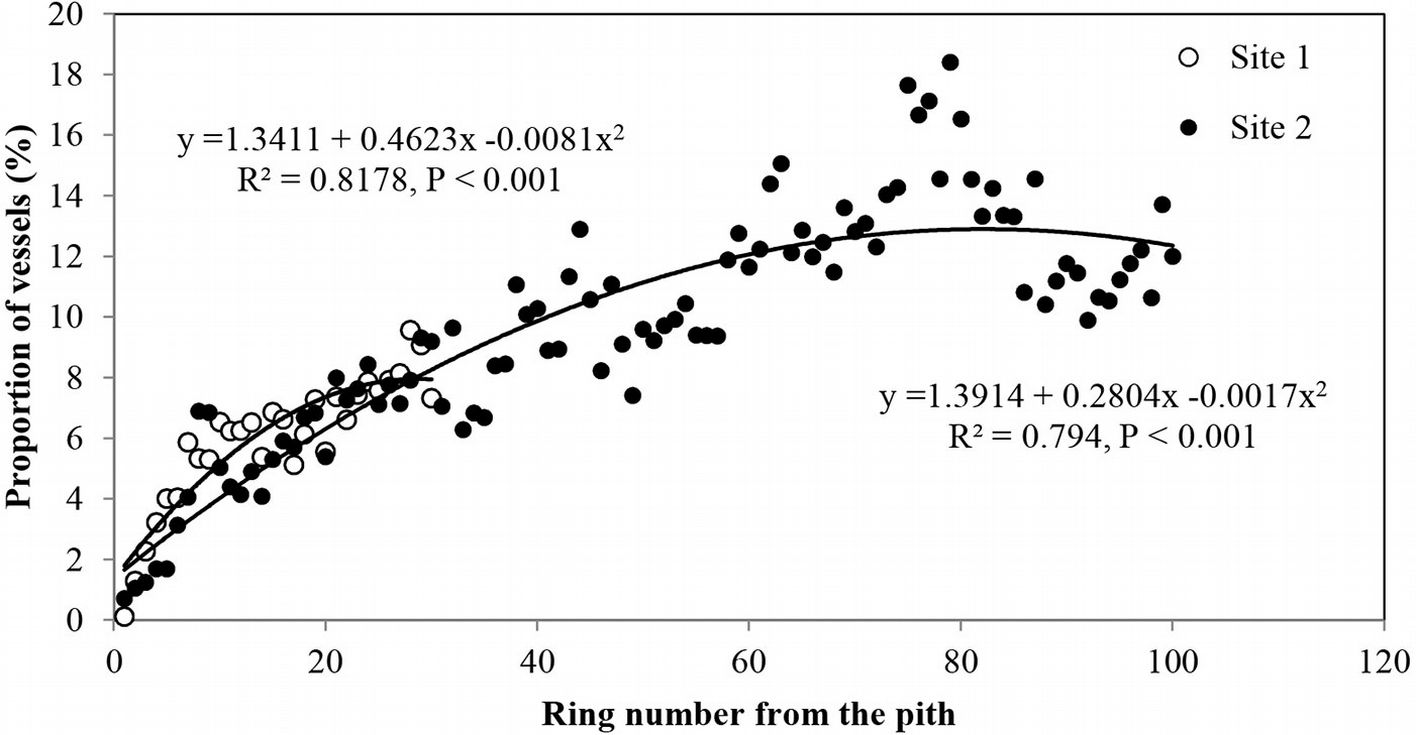
Vessel proportion showed an increase with age from the pith up to the 70th ring, with a maximum of 18.4% and then a slight decrease towards the bark (Fig. 6). This radial pattern was similar to that observed for the mean vessel area (Fig. 3a).
Fig. 6 - Radial profile of proportion of earlywood vessels per growth ring in Quercus faginea wood. Each point represents the mean of 10 trees at each site.
The proportion of vessels was related to ring width, i.e., the highest proportion was found in the narrowest rings and vice versa. Strong correlations were found between ring width and the number of vessels per ring (0.462 < r < 0.541), vessel frequency (-0.331 < r < -0.411) and vessel proportion (-0.425 < r < -0.557 - Tab. 2, Tab. 3, Tab. 4).
The best-fitted models for the prediction of earlywood vessel features based on ring width are presented in Fig. 7. Regardless of site, wider rings showed the higher number of vessels and the lower mean vessel area, vessel frequency and proportion.
Fig. 7 - Relationships between ring width and: (A) earlywood vessel area; (B) vessels number; (C) vessel frequency; and (D) vessel proportion in Quercus faginea wood at site 1 (S1) and 2 (S2). Each point represents the mean of 10 trees by each site.
Influence of earlywood vessel features on wood density
Considering the common period of 30 rings in the trees of the two sites, the mean wood density and the earlywood density were inversely correlated with the mean vessel area (r = -0.449, p < 0.01), as well as the mean wood density with the vessel proportion per ring (r = -0.367, p < 0.01). The number of vessels was negatively correlated with wood density (r = -0.166, p < 0.01) and earlywood density (r = -0.228, p <0.01). The correlation of vessel frequency with wood density was not significant (Tab. 4).
Overall, the wood density components (mean density, earlywood and latewood density) were inversely correlated with mean vessel area (-0.287, P < 0.01 < r < -0.449, P < 0.01) and vessel proportion (-0.254, P < 0.01 < r < -0.455, P < 0.01 - Tab. 2, Tab. 3, Tab. 4). The correlations between the wood density components and the number of vessels and vessel frequency were positive and weak within each site.
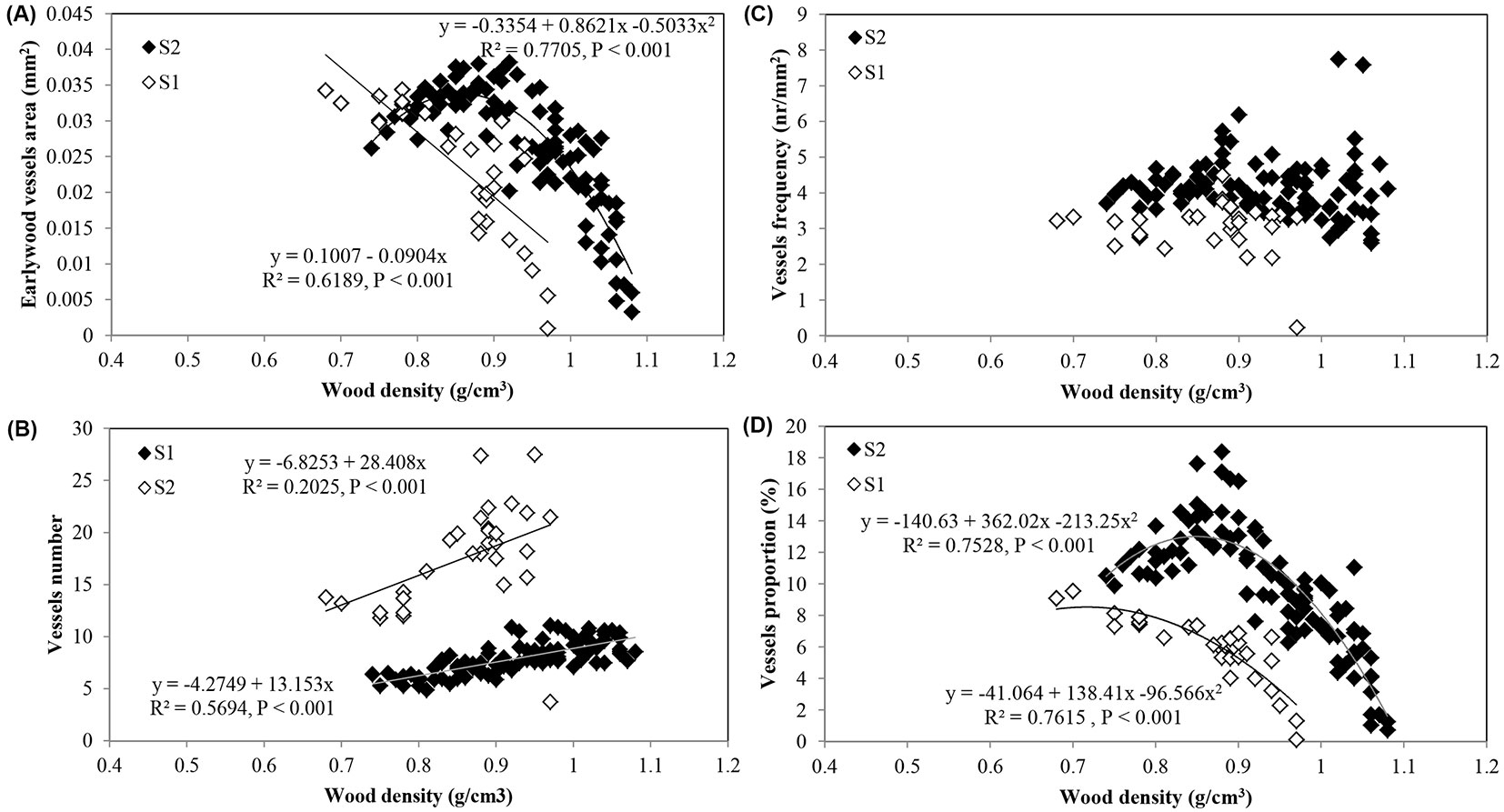
Fig. 8 shows the trend adjustment curves between the wood density and earlywood vessel features.
Fig. 8 - Relationships between wood density and; (A) earlywood vessel area; (B) vessels number; (C) vessel frequency; and (D) vessel proportion in Quercus faginea wood at site 1 (S1) and 2 (S2). Each point represents the mean of 10 trees by each site.
Discussion
In this study, the overall frequency distribution of vessel was left-skewed, as previously reported for Q. faginea ([41], [11], [2]), Q. robur and Q. ilex ([17], [5], [12]). The vessel distribution seems age-related, and the large number of small vessels in the initial years seem to be responsible of the above distortion.
The mean area of earlywood vessels observed in this study is consistent with the range of values (0.020-0.034 mm2) reported by Alla & Camarero ([2]) for Q. faginea. The area of vessels observed for this species was larger or similar as compared with other co-occuring evergreen oak species such as Q. coccifera, Q. ilex and Q. suber, but smaller than the vessel size reported for Q. robur and Q. petraea that less frequently co-occur with the portughese oak ([35], [41], [17], [24], [5]). It has been reported that vessel features and wood porosity are mainly affected by drought in the Mediterranean area ([10], [4]). In this study, the general climatic conditions are relatively similar in the two sample sites, even though they seemed more favorable at site 2. Nonetheless, vessel features were quite similar between the analyzed sites, as other factors affect drought tolerance of Q. faginea, such as the root system ([41]).
The increase of earlywood vessel area with cambial age in Q. faginea (Fig. 3a) has been also found in other oaks such as Q. suber ([24]), Q. garrayana ([26]), Q. macrocarpa ([19]) and Q. serrata ([40]) or in other non-related species such as Nothofagus nervosa ([13]).
The vessel number and vessel frequency are inversely related to average vessel area across species ([30], [29]). Consistently with previous reports ([2]), this was also the case in this study in Q. faginea (Tab. 2, Tab. 3, Tab. 4). The radial profile of the proportion of earlywood vessels of Q. faginea (Fig. 6) was similar to that found in Q. alba ([28]). Such increase of vessel proportion with ring number is related to the vessel diameter ([32], [36]). In this study, comparing the same age period between sites the vessel number and their area were higher in samples from site 1, likely due to tree- and/or site-specific factors. In Q. alba, also belonging to the white oaks sub-group as Q. faginea, Phelps & Workman ([28]) found that site quality was only expressed in the vessel proportion of trees at younger ages. According to Anfodillo et al. ([3]), tree size largely contributes to determine the vessel diameter, meaning that for the same age trees at site 1 seem to be taller showing wider vessels than trees grown at site 2. The decrease of ring width with age corresponded to a more constant vessel area and number, and to an increase of vessel frequency and proportion. The radial increase of vessel proportion is counterbalanced by a decreasing trend in the width of growth rings ([27], [23], [37]). The negative correlations between ring width and mean vessel area were stronger for narrower rings as they occurred at site 2 (Fig. 7). In contrast to our results, ring width in Fagus orientalis (semi-ring porous) and N. nervosa (diffuse porous) was also negatively correlated with vessel proportion and frequency, although positively correlated with mean vessel area ([13], [29]). Similarly, ring width in Q. alba (ring porous) was not correlated to the vessel proportion in earlywood ([28]). However, earlywood vessel features were explained to a lesser extent as function of ring witdh than as a function of age.
The inverse relationship between wood density and earlywood vessel area and proportion in Q. faginea (Fig. 8a) was clearly expected. Studies on several angiosperms reported that the average vessel area largely contributed to wood density variation, though a better relationship was found with the vessel proportion ([30], [31], [42]). In Q. faginea strong negative correlations were found between wood density and both mean vessel area and proportion. On the contrary, vessel frequency showed only weak correlations with wood density. Similar results were also obtained for Q. suber ([25]).
Our results demonstrate that vessel features partly explain the positive correlations between ring width and wood density reported by Knapic et al. ([23]), i.e., larger rings with less earlywood vessel area and proportion had higher density, in agreement with the radial decrease tendency of wood density and the weak correlation observed between wood density and latewood proportion in Q. faginea.
Conclusions
The ring porous wood of Q. faginea is due to the conspicuous occurrence of earlywood vessels, whose features are age-related. Vessel area increased with cambial age, while their number decreased with age. The radial patterns of the earlywood vessel features were similar between sites.
The earlywood vessel development in Q. faginea trees was related to some extent to radial growth. The negative correlation between mean wood density and both mean vessel area and proportion reflected the large impact of earlywood vessels on wood density in this species.
Acknowledgments
This study was partially supported by the Portuguese Project OAKWOODS (PTDC/ AGR-AAM/69077/2006) from the Portuguese Science Foundation (FCT) within the Fundo Europeu de Desenvolvimento Regional (FEDER) Programme. Forest Research Center (CEF) is a research unit funded by FCT under Pest-/AGR/UI239/2014. The authors would like to thank all the team involved on the project management, execution and fulfillment. Thanks to CITAB - Center for the Research and Technology of Agro-Environmental and Biological Sciences team for samples preparation and measurements, and P. Osório (ISA) for special help on vessel data organization. VBS acknowledges FCT for a doctoral fellowship.
References
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Gscholar
Authors’ Info
Authors’ Affiliation
Helena Pereira
Centro de Estudos Florestais, Instituto Superior de Agronomia, Universidade de Lisboa, Tapada da Ajuda, 1349-017 Lisboa (Portugal)
Departamento Florestal/CITAB, Universidade de Trás-os-Montes e Alto Douro, Quinta de Prados Apartado 202, 5000-911 Vila Real (Portugal)
Corresponding author
Paper Info
Citation
Sousa VB, Louzada JL, Pereira H (2015). Earlywood vessel features in Quercus faginea: relationship between ring width and wood density at two sites in Portugal. iForest 8: 866-873. - doi: 10.3832/ifor1346-008
Academic Editor
Francesco Ripullone
Paper history
Received: May 08, 2014
Accepted: Dec 31, 2014
First online: Apr 27, 2015
Publication Date: Dec 01, 2015
Publication Time: 3.90 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 52964
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 44925
Abstract Page Views: 2580
PDF Downloads: 4154
Citation/Reference Downloads: 27
XML Downloads: 1278
Web Metrics
Days since publication: 3837
Overall contacts: 52964
Avg. contacts per week: 96.62
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2015): 6
Average cites per year: 0.55
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Short Communications
Effect of intensive planting density on tree growth, wood density and fiber properties of maple (Acer velutinum Boiss.)
vol. 9, pp. 325-329 (online: 22 October 2015)
Research Articles
Physical, chemical and mechanical properties of Pinus sylvestris wood at five sites in Portugal
vol. 10, pp. 669-679 (online: 11 July 2017)
Research Articles
Validation of models using near-infrared spectroscopy to estimate basic density and chemical composition of Eucalyptus wood
vol. 17, pp. 338-345 (online: 03 November 2024)
Research Articles
NIR-based models for estimating selected physical and chemical wood properties from fast-growing plantations
vol. 15, pp. 372-380 (online: 05 October 2022)
Research Articles
Density, extractives and decay resistance variabilities within branch wood from four agroforestry hardwood species
vol. 14, pp. 212-220 (online: 02 May 2021)
Research Articles
Characterization of VOC emission profile of different wood species during moisture cycles
vol. 10, pp. 576-584 (online: 08 May 2017)
Research Articles
Interaction between planting spacing and wood properties of Eucalyptus clones grown in short rotation
vol. 14, pp. 12-17 (online: 02 January 2021)
Research Articles
The potential of using xylarium wood samples for wood density calculations: a comparison of approaches for volume measurement
vol. 4, pp. 150-159 (online: 11 August 2011)
Research Articles
Improving dimensional stability of Populus cathayana wood by suberin monomers with heat treatment
vol. 14, pp. 313-319 (online: 01 July 2021)
Research Articles
Physical and mechanical characteristics of poor-quality wood after heat treatment
vol. 8, pp. 884-891 (online: 22 May 2015)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword