Coupling daily transpiration modelling with forest management in a semiarid pine plantation
iForest - Biogeosciences and Forestry, Volume 9, Issue 1, Pages 38-48 (2015)
doi: https://doi.org/10.3832/ifor1290-008
Published: Aug 06, 2015 - Copyright © 2015 SISEF
Research Articles
Abstract
Estimating forest transpiration is of great importance for Adaptive Forest Management (AFM) in the scope of climate change prediction. AFM in the Mediterranean region usually generates a mosaic of different canopy covers within the same forest. Several models and methods are available to estimate forest transpiration, but most require a homogeneous forest cover, or an individual calibration/validation process for each cover stand. Hence, a model capable of reproducing accurately the transpiration of the whole canopy-cover mosaic is necessary. In this paper, the use of Artificial Neural Network (ANN) is proposed as a flexible tool for estimating forest transpiration using the forest cover as an input variable. To that end, sap flow, soil water content and other environmental variables were experimentally collected under five Aleppo pine stands of different canopy covers for two years. These sets of inputs were then used for the ANN training. Stand transpiration was accurately estimated using climate data, soil water content and forest cover through the ANN approach (correlation coefficient R = 0.95; Nash-Sutcliffe coefficient E = 0.90; root-mean-square error RMSE = 0.078 mm day-1). Finally, the input value for soil water content (when not available) was computed using the process-based model Gotilwa+. Then, this computed soil water content was used as input in the proposed ANN. This combination predicted the forest transpiration with values of R = 0.90, E = 0.63, and RMSE = 0.068 mm day-1. Artificial Neural Network proved to be a useful and flexible tool to predict the transpiration dynamics of an Aleppo pine stand regardless of the heterogeneity of the forest cover produced by adaptive forest management.
Keywords
Adaptive Forest Management, Artificial Neural Network (ANN), Forest Water-use, Pinus halepensis Mill.
Introduction
Transpiration is one of the most important components in the terrestrial water cycle, representing 80-90% of terrestrial evapotranspiration ([36]). In Mediterranean ecosystems, it may account for about three-quarters of the overall forest evapotranspiration on an annual basis ([43]). Thus, the role of transpiration in the water fluxes and within the soil-vegetation-atmosphere system is crucial to understand forest-water use and to implement proactive and adaptive measures in forests, in purview of the global change ([3], [26], [65]). This is particularly important in Mediterranean ecosystems, which are extremely vulnerable to global climate change ([35], [46], [67]).
Adaptive forest management (AFM) in Mediterranean ecosystems seeks to couple the concept of ecophysiology with the dryland forests management techniques, through the development of an ecosystem-level water balance ([65]). In the Mediterranean Spain, AFM may improve stand resilience and the balance between green (ecosystem needs) and blue (available for human use) water budgets ([24]) in Pinus halepensis Mill. (Aleppo pine) reforestations ([21]), which occupy over 5×105 ha of the region ([9]). Thus, prediction of forest transpiration under different forest management scenarios represents a key factor for successful and appropriate AFM design in Mediterranean Spain.
Modeling the factors that influence transpiration is quite complex due to the existence of non-linear and complex interactions ([3]). The fundamental controls are the available water in the soil, the ability of plants to transfer water from the soil to leaves and the capacity of the atmosphere to absorb the transpired water ([18]).
Forest transpiration may be estimated using different approaches. Dekker et al. ([19]) reported that by considering all different types of process-orientated forest transpiration models, four different perspectives can be deduced: cooling of leaves, assimilation of CO2, energy balance and water balance. All of these perspectives show a wide variation in physiological details. However, the most widely used transpiration models are based on the energy balance, which are mostly derived from the Penman-Monteith’s equation. They generally constitute the Process Based Models (PBM). Nevertheless, these approaches are Big-Leaf models, whose application requires the assumption of a homogeneous forest cover or an individual calibration/validation process for each stand. Since the application of AFM usually leads to a mosaic of different forest cover and structures within the same forest, it is paramount to use of a method capable of including such heterogeneity.
Artificial Neural Network (ANN) techniques represent an attractive modeling approach to deal with this issue, as forest cover heterogeneity can easily be included as an input variable. ANN is a flexible mathematical structure, which is capable to identify complex nonlinear relationships between the input and output data sets. Furthermore, ANN models are considered useful and efficient, particularly when the characteristics of the processes are difficult to describe using physical equations (i.e., when the relationship between input and output variables is not explicit - [61]). ANNs map the implicit relationship between inputs and outputs through training on field observations ([60]). Furthermore, ANN usually achieves regression coefficient around 0.90, thus performing more accurately than other approaches such as statistical or PBM.
In recent years, ANNs have intensively been applied in forest and agriculture hydrology, e.g., in estimating evapotranspiration ([40], [41], [1], [33]), trunk sap flow ([47]) and transpiration ([73], [74], [69], [27], [28], [50], [45]). In forest management, ANNs have also been applied to estimate tree volume ([29], [62], [23], [54], [55], [72]), growth modeling ([15]), tree height ([7]), and to describe diameter distribution ([44], [8]). However, none of these applications include forest management as an input variable, at least in the estimation of transpiration. The use of this variable would: (i) extend capabilities and use of ANN-based modeling; (ii) allow a more accurate determination and quantification of the influence of forest management practices on transpiration; (iii) increase the resilience of forests to new climate conditions.
Despite the aforementioned advantages, ANN have some limitations, e.g., it cannot be applied when some of the required input data are not available to forest managers. Under such circumstances a combination of ANN and PBM can be a useful alternative. Although their sophistication theoretically allow to reproduce the complex dynamics of forest ecosystems in details, it makes also difficult their use and evaluation ([66]). Hence, PBM could be used in some cases to feed ANN when the estimate of the required input data is not readily available.
In this study, we aimed to develop a reliable model to estimate transpiration in forest stands considering explicitly the influence of forest management as an input variable. More specifically, we intended: (i) to explore the relationships between measured forest transpiration and explicative environmental variables to define the most reliable empirical model (Linear Models and ANN-based approaches); (ii) to incorporate forest cover as a forest management-derived variable into the chosen modeling approach and to evaluate its predictive ability; (iii) to evaluate the model performance when soil moisture has to be derived from other modeling approaches (Gotilwa+).
Material and methods
Sap flow, soil water content and other environmental variables were recorded for two years in five Aleppo pine stands (see below) with different canopy covers. First, a Multiple Linear Regression (MLR) and a General Linear Model (GLM) using field data were developed and validated to analyze the performance of both models in predicting transpiration. Subsequently, an ANN modeling scheme was used to estimate the stand transpiration using climate data, soil water content and forest cover as input variables. When soil water content data was not available (only for medium intensity thinning stand), it was first computed using the process-based model Gotilwa+ and then used as an input value in the modeled ANN.
Study site and data collection
The study site is a public forest of 4682 ha located in the Ayora valley region (39° 5′ N, 1° 13′ W, 943 m a.s.l.) in the Southwest of Valencia province (Spain). The climate is Mediterranean with an average total annual rainfall of 478 mm and a mean annual temperature of 13.7 °C (1960-2010). Soils are Calcisols, derived from Triassic limestone (gravel and boulders) with high percentage of carbonates (26-38%, pH 7.7-8.2) and sandy-silty loam texture. Part of the area (22%) is covered by Pinus halepensis Mill. stands 50-60 years old, with high tree density (approx. 1500 trees ha-1) mainly due to low forest management. Detailed information about the study site is available elsewhere ([51]).
In 2008, an experimental thinning was performed in four 30 × 30 m plots, reducing the forest cover from 84% (C: control plot) to 22% (H: high intensity plot), 50% (M: medium intensity plot) and 68% (L: low intensity plot). In addition, a nearby area thinned in 1998 (H98) with 41% cover was included in this study and considered as the temporal evolution of the high intensity (H) treatment (Tab. 1). Overall, five distinct plots with different forest covers were considered in this work.
Tab. 1 - Characteristics of control and thinned plots. (DBH): diameter at breast height; (H98): plot thinned in 1998 (plots L, M and H were thinned in 2008). Adapted from Molina & Del Campo ([51]).
| Thinning Treatment | Forest Cover (%) |
Density (trees ha-1 ) |
DBH (cm) |
Height (m) |
|---|---|---|---|---|
| Control (C) | 84 | 1489 | 17.8 ± 5.1 | 11.5 |
| Low intensity (L) | 68 | 744 | 21.2 ± 4.1 | 12.2 |
| Medium intensity (M) | 50 | 478 | 21.7 ± 4.0 | 11.3 |
| High intensity (H) | 22 | 178 | 20.4 ± 1.6 | 12.2 |
| High intensity-1998 (H98) | 41 | 155 | 25.2 ± 5.0 | 12.6 |
Forest cover was measured in each plot with a vertical densitometer (GRS, Arcata, CA, USA) with 50 readings per plot in a 4 × 4 m grid. Hydrological (transpiration and soil moisture) and environmental variables (T: air temperature in °C; Sr: solar radiation in MJ m-2 day-1; Ppt: rainfall in mm; RH: relative humidity in %; and Ws: wind speed in m s-1) were collected from June 2009 to March 2011 (Tab. 2). Measurements of Ppt, T, and RH were carried out by a single sensor (HR/T sensor, Decagon Devices, Pullman, USA) placed 1 m above the ground and close to the treatment plot. Values were recorded and averaged every 30 minutes. Afterward, these data were used to obtain values for mean, maximum and minimum daily temperature and vapor pressure deficit (VPD - [2]).
Tab. 2 - Mean values ± standard deviation of the recorded variables in each treatment (years 2009-2011). (N): number of days available for analysis; (Tr): Transpiration (mm day-1); (SWC): average daily soil water content (cm3 cm-3); (Ppt): precipitation (mm); (Tmax, Tmin and T): maximum, minimum and mean temperature, respectively (oC); (RH): relative humidity; (VPD): vapour pressure deficit (kPa); (Ws): wind speed (m s-1); (Sr): solar radiation transformed in equivalent evaporation (mm day-1). Solar radiation expressed in MJ m-2 day-1 was converted to equivalent evaporation in mm day-1 as the inverse of the latent heat of vaporization (1/L = 0.408 - [2]).
| Variable | Thinning intensity |
2009 | N | 2010 | N | 2011 | N |
|---|---|---|---|---|---|---|---|
Tr
|
High | 0.44 ± 0.26 | 187 | 0.34 ± 0.20 | 309 | 0.14 ± 0.10 | 90 |
| High-1998 | 0.29 ± 0.15 | 187 | 0.22 ± 0.13 | 128 | - | 90 | |
| Medium | - | - | 0.19 ± 0.12 | 99 | 0.13 ± 0.09 | 90 | |
| Low | 0.31 ± 0.18 | 187 | 0.38 ± 0.26 | 309 | 0.19 ± 0.14 | 90 | |
| Control | 0.32 ± 0.26 | 187 | 0.47 ± 0.36 | 309 | 0.25 ± 0.19 | 90 | |
SWC
|
High | 0.19 ± 0.06 | 187 | 0.26 ± 0.06 | 309 | 0.28 ± 0.02 | 90 |
| High-1998 | 0.11 ± 0.04 | 187 | 0.19 ± 0.03 | 128 | 0.20 ± 0.03 | 90 | |
| Low | 0.13 ± 0.07 | 187 | 0.19 ± 0.06 | 309 | 0.19 ± 0.04 | 90 | |
| Control | 0.15 ± 0.07 | 187 | 0.22 ± 0.06 | 309 | 0.22 ± 0.03 | 90 | |
T max |
- | 23.2 ± 9.42 | 187 | 20.1 ± 8.94 | 309 | 11.0 ± 4.33 | 90 |
T min |
- | 11.2 ± 6.08 | 187 | 8.5 ± 5.91 | 309 | 2.3 ± 3.43 | 90 |
T
|
- | 16.9 ± 7.52 | 187 | 13.9 ± 7.16 | 309 | 6.1 ± 3.22 | 90 |
RH
|
- | 0.6 ± 0.20 | 187 | 0.7 ± 0.15 | 309 | 0.8 ± 0.12 | 90 |
VPD
|
- | 1.0 ± 0.88 | 187 | 0.7 ± 0.59 | 309 | 0.3 ± 0.17 | 90 |
Ppt
|
- | 1.5 ± 4.32 | 187 | 1.8 ± 4.67 | 309 | 1.9 ± 5.06 | 90 |
Ws
|
- | 2.3 ± 1.32 | 187 | 2.3 ± 1.30 | 309 | 2.4 ± 1.53 | 90 |
Sr
|
- | 7.7 ± 3.81 | 187 | 7.2 ± 3.35 | 309 | 4.8 ± 2.11 | 90 |
Daily values for solar radiation and wind speed were obtained from the Almansa weather station, located near the study site. Transpiration was measured using sap flow sensors (HRM-30, ICT International Pty Ltd., Armidale, Australia - [13]) in four trees per plot according to the diametric distribution of trees in the plot. In the conversion of the heat pulse velocity to sap flow velocity, raw values were corrected for probe misalignment ([13]) and differences in thermal diffusivity and wounding by examining the samples under a light microscopy ([4]). Baseline correction in the obtained series was performed according to Buckley et al. ([12]).
The accumulated daily values of sap flow (water transpired by the entire tree) were estimated considering a radial distribution of the sap flux velocity in the sapwood of each selected tree ([22]). The sapwood area per tree was measured after extracting samples with an increment core (5 mm) and measuring to the nearest 0.01 mm with a measuring table (LINTAB 6.0, Frank Rinn, Heidelberg, Germany) coupled with the TSAP-Win® software package ([58]). Total transpiration by the pine forest (Tr, mm day-1) per treatment was calculated by multiplying the daily transpiration (L, day-1 tree-1) by the frequency of diameter class (f) and the stand density (trees ha-1) by the following equation (eqn. 1):
where Trn is the daily transpiration of each treatment (mm day-1), fn is the frequency of each tree class measured, N is the number of trees in the stand (Tab. 1), and the denominator 10000 is for conversion of litters ha-1 into mm.
Soil water content (SWC, cm3 cm-3) was measured every 20 minutes by capacitance sensors (Echo, Decagon Devices Inc., Pullman, WA, USA) and averaged to a daily value. In each treatment, three sensors were placed under the crown-projected area at 30 cm depth beneath two randomly selected trees out of the four trees sampled for transpiration. The daily values of the sensors were individually calibrated, averaged and converted to obtain the daily value per treatment. Tab. 2 summarizes the different data collected in the present study.
The medium intensity treatment (M) presented numerous data gaps for most variables (including transpiration and soil moisture). For this reason, M was chosen to test the model performance with the derived variable (SWC) generated by PBM (objective iii). Hence, this treatment was discarded for model building, evaluation and validation either with linear or ANN techniques.
Transpiration
Multiple Linear Regression (MLR) and General Linear Models (GLM)
Artificial neural networks are widely considered as a powerful tool in the identification of highly non-linear systems, like the target variable in this study (daily transpiration). Nonetheless, a more traditional approach based on multiple linear regression (MLR) is also presented, providing an interesting modeling benchmark using appropriate final performance index (see below). Not only this classical, well known MLR approach was used, but also a linear regression was implemented through a simplified neural network with only two layers and linear nodes, which will be referred in the following as general linear model (GLM - [56]). These two models (MLR and GLM) represent an adequate benchmark to evaluate the relative merits and performance of the neural network approach ([56], [47]). Both methods were individually applied to each treatment (C, L, H and H98), as well as to the data pooled together, including the forest cover as an input variable. In all cases, the target variable to be predicted was daily transpiration. Concerning input variables, a correlation analysis and a stepwise method was previously performed to assess variable selection process, which is common to both the approaches (MLR and GLM).
Transpiration based on Artificial Neural Network
Artificial neural network (ANN) modeling process comprises three stages: pre-processing (including variable selection, data division, data scaling and normalization), processing (ANN architecture and network training process) and post-processing or model evaluation ([29]). In each of the mentioned stages, the criteria listed in the next chapters were used.
Stage 1: Data pre-processing
A proper selection of relevant inputs for ANNs is important as they strongly influence the final performance of the model, particularly when interrelationships between predictor variables are known to occur.
The most relevant variables affecting the final transpiration rates are VPD, Sr, RH, T, Ws, LAI ([47]), although the physical mechanisms involving groups and subgroups of variables acting simultaneously are complex non-linear processes. This fact makes the choice of optimal predictor variables difficult. For this purpose, a sensitivity analysis was conducted to avoid combinations of input variables that might yield an ill-conditioned system ([63]). Different groups of input variables were tested in order to find the best combinations for improved transpiration rate predictions.
The first issue using an ANN modeling strategy is the division of the dataset into the training and the test subsets, as it can significantly affect the selection of optimal ANN structure and the evaluation of its forecasting performance ([75]). A third data subset, usually named cross-validation set, is also used to avoid over-training problems or to determine the stopping point of the training process. Although no clear guidelines do exists for selecting the relative size of such subsets, we adopted the commonly used criterion of setting the size of the training set as 70% of the whole dataset, reserving the remaining data for the test (15%) and cross-validation (15%) sets.
Obviously, the use of representative subsets is of significant importance for the performance of the neural network and its final generalization capability. To account for it, transpiration data for each treatment were previously classified into four classes, with class limits set at (μ-σ), μ and (μ+σ), where μ is the average value and σ is the standard deviation. For each class, data were then classified considering the VPD range and the different seasons separately. Finally, a t-test was applied to the training, test and cross validation sets to test for differences between sample means. No significant statistical differences between sample means (p<0.05) were found.
The variables under consideration in this research span different ranges. In order to ensure that all variables receive equal attention during the ANN training process, the original data were transformed to the interval [0;1], with the exception of forest cover and VPD, according to the following equation (eqn. 2):
where xnorm is the normalized value, x0 is the original value, x is the average value of the original series, and xmax and xmin are its maximum and minimum value, respectively.
In the case of forest cover, no transformation was required as original values already lie in the interval [0;1]. The second exception is VPD variable. In neural network modeling, the probability distribution of input data does not need to be strictly known ([14]), although in some cases a skew reduction in the original data can be desirable, particularly when it is very significant. In present study, this was the case of the variable VPD, which was transformed with an exponential function (eqn. 3):
Obviously the direct output of the neural network (transpiration) is a scaled or normalized value, which needs to be converted to its original range before proceeding to the model performance evaluation procedure ([64]).
Stage 2: ANN architecture and training algorithm
In this study a feed-forward artificial neural network (FFNN) is proposed as a mathematical model to predict forest transpiration rates. It consists of a set of sensory units that constitute the input layer, one or more hidden layers of computational nodes and an output layer of computational nodes producing the output of the network ([31]). Information passes only in one direction, from the input nodes to those in the succeeding layers up to the output layer. The strength of connections between nodes of successive layers is represented by the weight values, acting as parameters of the neural network model.
In general, the output layer has as many nodes as target variables. In our case, it will include only one node, corresponding to the sole target variable (daily transpiration). Concerning the number of hidden layers, no consolidated theory currently exists on the number of hidden layers needed for accurate predictions, although it has been proved that only one layer of hidden units with non-linear nodes is sufficient to approximate any function to an arbitrary level of precision ([32]). Accordingly, a topology of three layers with a single output node in the third layer was designed. The number of nodes i in the input layer is the number of predictor variables used.
A common problem in FFNN building is the specification of the number of nodes required in the hidden layer. It is worth to notice that the more complex is the mapping between the variables, the larger is the number of hidden nodes required. In this study, a range of neural networks were tested varying the number of hidden nodes from i/2 to 2i, in order to select the optimal dimension of the network. In a similar way, a family of activation functions in the hidden and output layer were tested (logistic, hyperbolic tangent, and exponential for the hidden layer; exponential and identity function in the output node - [69], [50], [47]).
The training algorithm can be addressed as an unconstrained non-linear minimization problem in which weight values are iteratively modified to minimize the overall mean squared error between the desired and actual output values of scaled transpiration. A variety of powerful algorithms are reported in the literature, but in practice none of them guarantee the global optimal solution for a general nonlinear optimization problem, with efficiency and computational performance depending largely on the structure and characteristics of the unknown error function.
For most practical applications, the faster convergent and more efficient algorithms are the second-order methods, like the Broyden, Fletcher, Goldfarb and Shanno (BFGS), Levenberg-Marquardt and conjugate gradient ([75]), although first-order method algorithms have also been successfully used in many relevant applications. Therefore, some popular methods were initially tested in our network, including the well-known standard backpropagation algorithm with variable learning rate ([40]), the resilient backpropagation ([57], [34]), and the backpropagation algorithm with weight decay ([6]). However, in our case BFGS algorithm provided apparently better performance, showing faster training and superior generalization abilities of the resulting networks ([68], [34], [53], [37]). This powerful technique is particularly suitable when a large number of topologies and activation functions are to be tested, as it was the case in this study. To avoid weights with high values in the selected networks, a regularization weight decay procedure was incorporated in the training process ([10]), that essentially consists of an addition of a term to the error function, penalizing the solutions with large weight values.
Stage 3: Model evaluation
The accuracy of predictions of the observed transpiration values can be measured using a variety of metrics, thus assessing the performance of the different models tested. Common statistics were computed, including R, E and RMSE (see below), no matter the type of model under examination.
Process-based model
In this study, the PBM GOTILWA+ was applied to estimate SWC, a variable that might not be readily available to forest managers. GOTILWA+ is an improved version of GOTILWA described by Gracia et al. ([30]) and Kramer ([38]). It can estimate accurately the water flux of Mediterranean forest ecosystems (different single-tree species stands: coniferous or broadleaved, evergreen or deciduous) under changing environmental conditions, due to either climate or forest management. For this reason, GOTILWA+ was used here to estimate both transpiration (directly) and soil water content (to fed the ANN).
This model requires a number of inputs to simulate forest growth parameters at a daily time scale. The inputs describe the forest structure and physiology, soil and climate conditions. The forest structure was considered heterogeneous in terms of diametrical distribution, which was defined according to the initial tree inventory. Leaf photosynthesis and stomata conductance parameters for Pinus halepensis were included in the GOTILWA+ model based on measured data from experimental plots in Collserola (Catalonia - data available at ⇒ http://www.creaf.uab.es/gotilwa+/SParameters.htm). Soil parameters were obtained from an earlier study ([20]). Daily climatic data were obtained as previously described. GOTILWA+ performance was analyzed comparing the measured and estimated transpiration with soil moisture values, considering the index of model evaluation (see below).
Model evaluation
For comparisons between the measured and simulated transpiration using the ANN model, the multiple-linear regression (MLR), the general linear models (GLM) and GOTILWA+, three indexes were used: (i) the coefficient of correlation (R, eqn. 4); (ii) the Nash-Sutcliffe Efficiency (E, eqn. 5), which compares the performance of the model to a model that only uses the mean of the observed data (1 = perfect model; 0 = performance no better than simply using the mean; negative values = bad performance - [5]); and (iii) the root mean squared error (RMSE, eqn. 6), which measures the deviation of model predictions from the observed data ([71] - eqn. 4, eqn. 5, eqn. 6):
where n is the number of data considered, Yobs_i is the daily transpiration observed by heat pulse method for the i-th value, Ysim_i is the simulated transpiration for the i-th value, Yobs and Ysim are the average values of corresponding variables, respectively. In addition, a graphical analysis was used to compare and verify presence of heteroscedasticity in the dataset.
Results
Linear analysis
The linear correlation matrix between input variables and daily transpiration showed that correlations differ significantly among the different treatments (plots) considered in this study (Tab. 3). Correlation values tend to be higher for intensive thinning, and lowest for the control treatment. It should be noted that in the case of strongly physically interrelated variables (i.e., VPD and transpiration), expected high values can be as low as 0.29 for the control treatment. Other variables, such as wind speed, precipitation and soil water content, showed negative, modest correlations in both individual treatments and grouped data. Based on these results, it follows that some variables do not significantly contribute to explain transpiration (e.g., Ws, which was not further considered). On the other hand, the co-linearity between variables made advisable to consider only those showing the highest correlations (as in the case of RH with Ppt).
Tab. 3 - Linear correlation matrix between input variables and daily transpiration (mm) in each treatment. (Tmax, Tmin and T): maximum, minimum and mean temperature, respectively (oC); (RH): relative humidity; (VPD): vapour pressure deficit (kPa); (Ppt): precipitation (mm); (Ws): wind speed (m s-1); (Sr): solar radiation, transformed in equivalent evaporation (mm day-1); (SWC): average daily soil water content (cm3 cm-3).
| Treatment | T max |
T min |
T
|
RH
|
VPD
|
Ppt
|
Ws
|
Sr
|
SWC
|
|---|---|---|---|---|---|---|---|---|---|
| High intensity | 0.86 | 0.75 | 0.84 | -0.76 | 0.82 | -0.32 | -0.17 | 0.85 | -0.35 |
| High intensity-1998 | 0.82 | 0.69 | 0.79 | -0.75 | 0.73 | -0.47 | -0.27 | 0.76 | -0.31 |
| Low intensity | 0.58 | 0.45 | 0.55 | -0.53 | 0.46 | -0.28 | -0.16 | 0.64 | 0.03 |
| Control | 0.42 | 0.30 | 0.38 | -0.40 | 0.29 | -0.25 | -0.14 | 0.53 | 0.22 |
| All grouped | 0.59 | 0.47 | 0.56 | -0.53 | 0.49 | -0.29 | -0.16 | 0.63 | 0.02 |
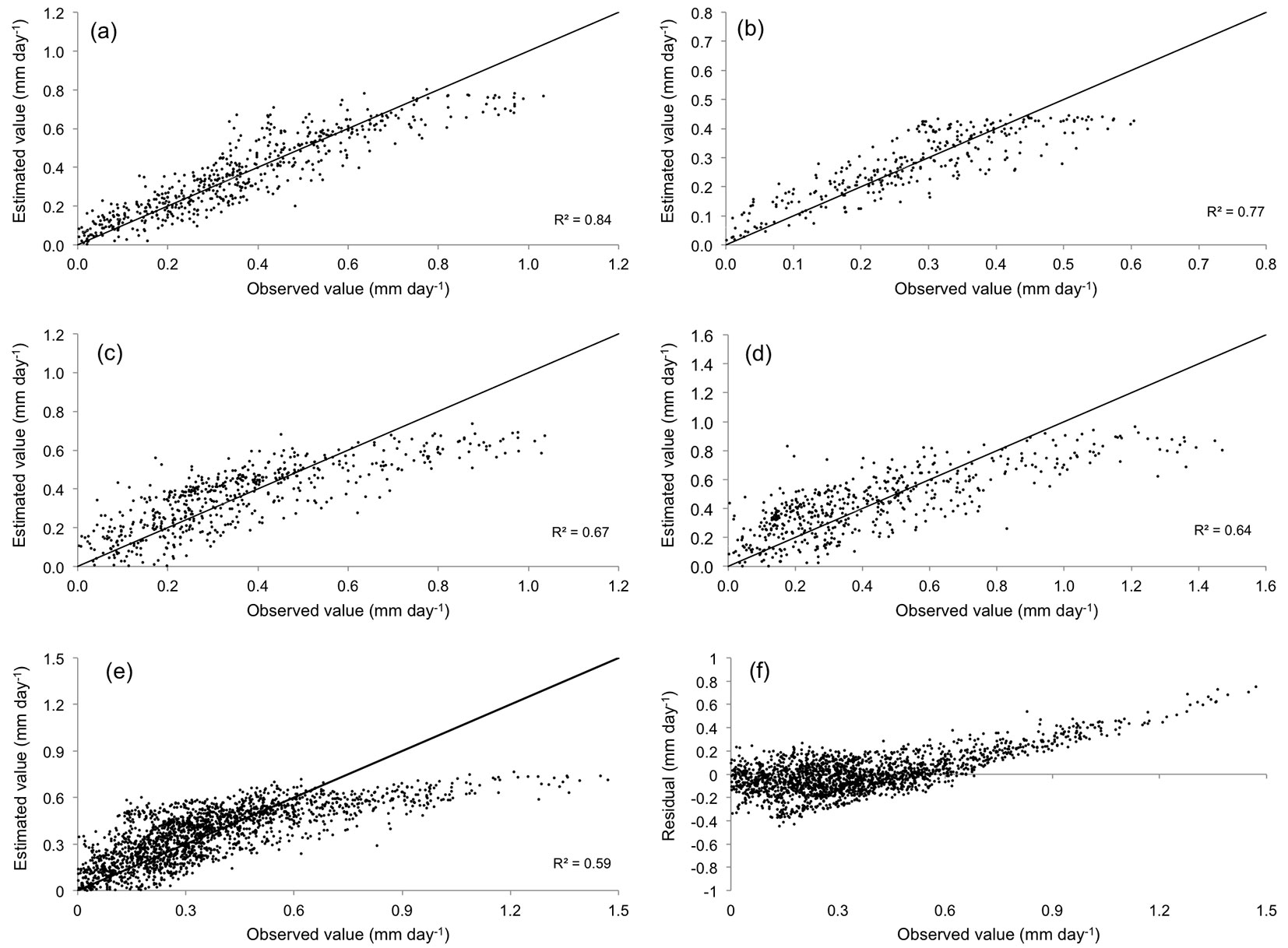
Linear based models (MLR and GLM) were developed for transpiration estimation, both for each individual treatment and for the grouped treatments. In total, ten different models were formulated by varying the input variables under consideration. For each model, R, RMSE and E values were computed (Tab. 4), attaining fairly similar performances using both the MLR and GLM approaches. This was expected as both models comprise essentially a linear regression between inputs and output. On the other hand, the type of treatment was affecting significantly the prediction ability of the models, with E coefficient ranging from 0.63 to 0.84 (Tab. 4). Fig. 1 shows the estimated vs. observed values of transpiration obtained by MLR. Although results can reasonably be acceptable, a systematic underestimation was detected for larger values of transpiration, regardless the treatment considered (Fig. 1a-d). The inclusion of an input variable related to forest management (forest cover) did not improve the model performances in either case (GLM nor MLR, All grouped - Tab. 4). Conversely, such inclusion decreased both the Nash-Sutcliffe (E < 0.6) and the R coefficients, worsening the model’s predictive ability at high transpiration values (Fig. 1e-f). However, the stepwise procedure of MLR showed better results than GLM on the pooled data (Tab. 4), although Tmin was used as input only in H98 and L treatments.
Tab. 4 - Goodness-of-fit statistics for Multiple Linear Regression (MLR) and General Linear Method (GLM). (R): correlation coefficient; (RMSE): root mean squared error;(E): Nash-Sutcliffe efficiency; (Tmax, Tmin and T): maximum, minimum and mean temperature, respectively; (RH): relative humidity; (VPD): vapour pressure deficit; (Sr): solar radiation; (SWC): soil water content; (Cover): forest cover.
| Model | Treatment | R | RMSE | E | Inputs |
|---|---|---|---|---|---|
| MLR | High intensity | 0.91 | 0.093 | 0.84 | Tmax, T, Sr, RH, SWC |
| High intensity-1998 | 0.87 | 0.071 | 0.76 | Tmax, Tmin, Sr, RH,VPD, SWC |
|
| Low intensity | 0.81 | 0.135 | 0.66 | Tmax, Tmin, T, Sr, RH, VPD, SWC |
|
| Control | 0.79 | 0.194 | 0.63 | Tmax, T, Sr, RH, VPD, SWC |
|
| All grouped | 0.77 | 0.161 | 0.59 | Tmax, T, Sr, RH, VPD, SWC, Cover |
|
| GLM | High intensity | 0.91 | 0.093 | 0.84 | Tmax, Tmin, T, Sr, RH, VPD, SWC |
| High intensity-1998 | 0.87 | 0.071 | 0.76 | Tmax, Tmin, T, Sr, RH, VPD, SWC |
|
| Low intensity | 0.81 | 0.135 | 0.66 | Tmax, Tmin, T, Sr, RH, VPD, SWC |
|
| Control | 0.79 | 0.193 | 0.63 | Tmax, Tmin, T, Sr, RH, VPD, SWC |
|
| All grouped | 0.75 | 0.166 | 0.56 | Tmax, Tmin, T, Sr, RH, VPD, SWC, Cover |
Fig. 1 - Observed vs. estimated values of stand transpiration by Multiple Linear Regression. (a): High intensity thinning treatment; (b): high intensity 1998; (c): low intensity; (d): control; (e): all treatments pooled; (f): residual values for all treatments pooled.
Transpiration based on ANN
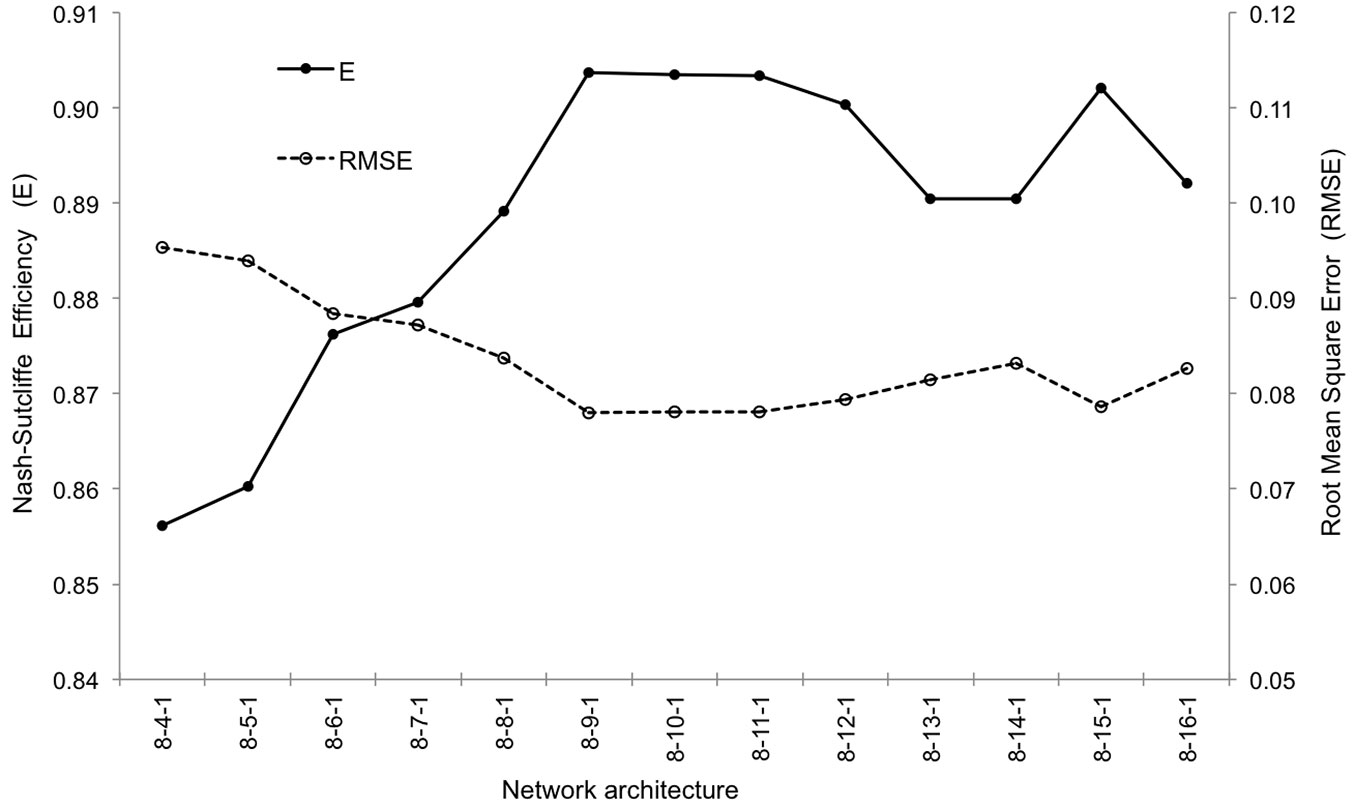
A sensitivity analysis was conducted to identify the importance of different predictors used for estimating the forest transpiration. The error function showed the greatest increase when SWC (soil moisture) was dropped out from the model, and thus it was considered as a key variable in the input family. The two subsequent variables that most affected the prediction error were Sr and Tmax. All the ANN models tested included these three variables, while all other predictors were included following a stepwise procedure. The best results were achieved when the input family included the variables Tmax, Tmin, Tmean, Sr, RH, VPD, SWC and Cover (Tab. 5). The optimal number of hidden nodes (nh) for the best network performance was 9, thus the network 8-9-1 was finally selected. Fig. 2 shows the values of E and RMSE after training the networks with the different sizes of the hidden layer. Concerning the activation function, the best results were attained using a hyperbolic tangent function in the hidden nodes and an exponential function in the single node of the output layer.
Tab. 5 - Comparison between measured and simulated transpiration for each treatment, using the selected Artificial Neural Network (8-9-1). Last row represents the ANN general performance. (R): correlation coefficient; (RMSE): root mean squared error; (E): Nash-Sutcliffe Efficiency; (Tmax, Tmin and T): maximum, minimum and mean temperature, respectively; (RH): relative humidity; (VPD): vapour pressure deficit; (Sr): solar radiation; (SWC): soil water content; (Cover): forest cover.
| Treatment | R | RMSE | E | Inputs |
|---|---|---|---|---|
| High intensity | 0.96 | 0.065 | 0.92 | Tmax, Tmin, T, Sr, RH, VPD, SWC, Cover |
| High intensity-1998 | 0.91 | 0.060 | 0.82 | |
| Low intensity | 0.94 | 0.081 | 0.88 | |
| Control | 0.96 | 0.092 | 0.91 | |
| All grouped | 0.95 | 0.077 | 0.90 |
Fig. 2 - Nash-Sutcliffe efficiency (E) and root mean square error (RMSE) of the different architectures of the tested artificial neural network.
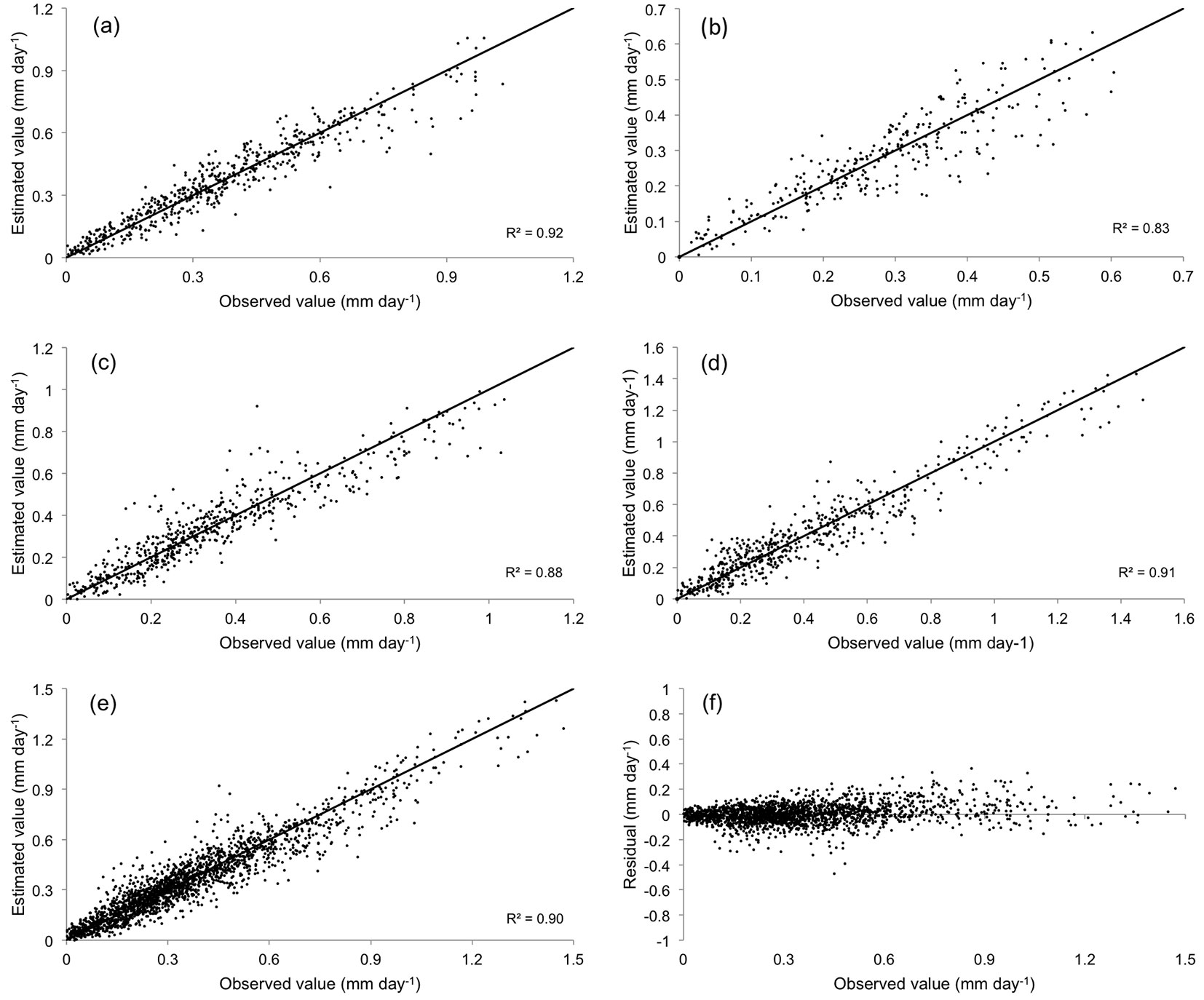
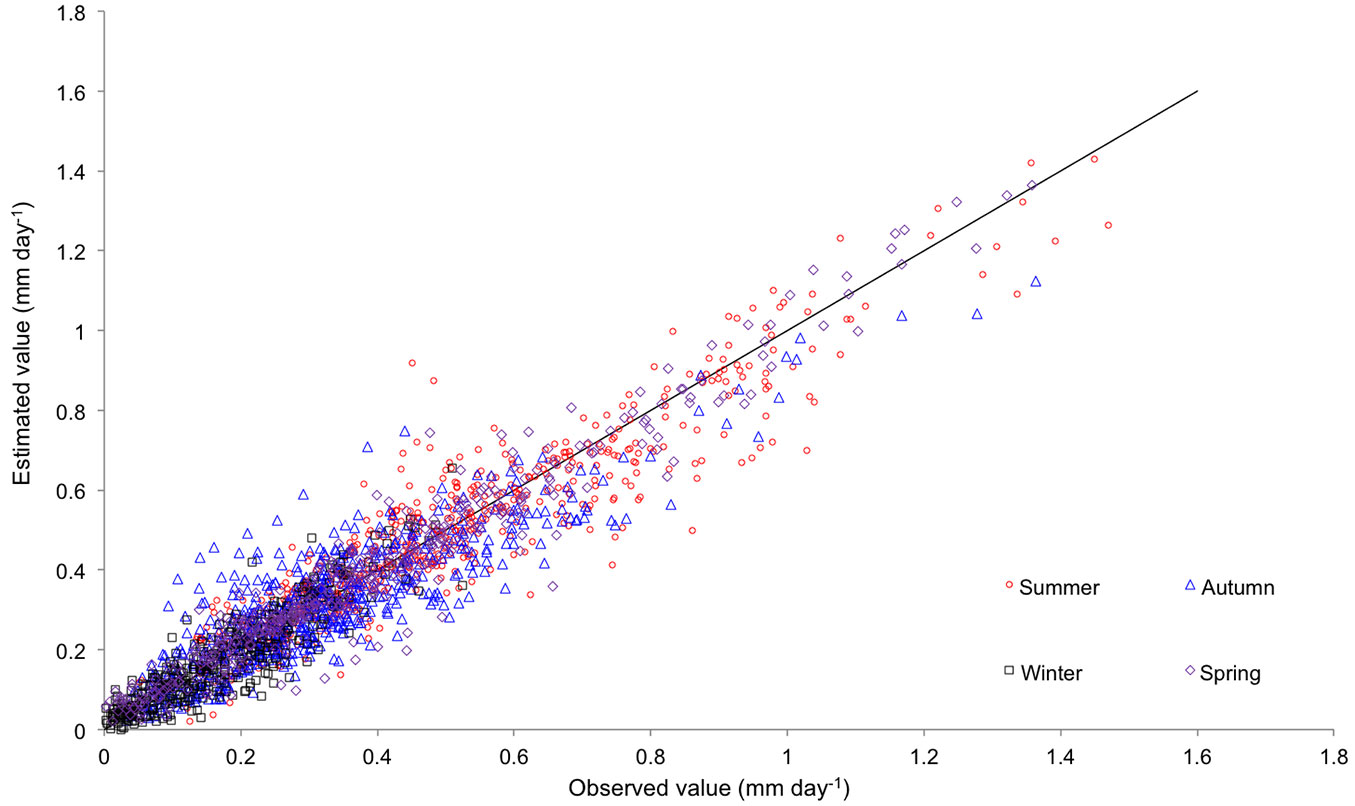
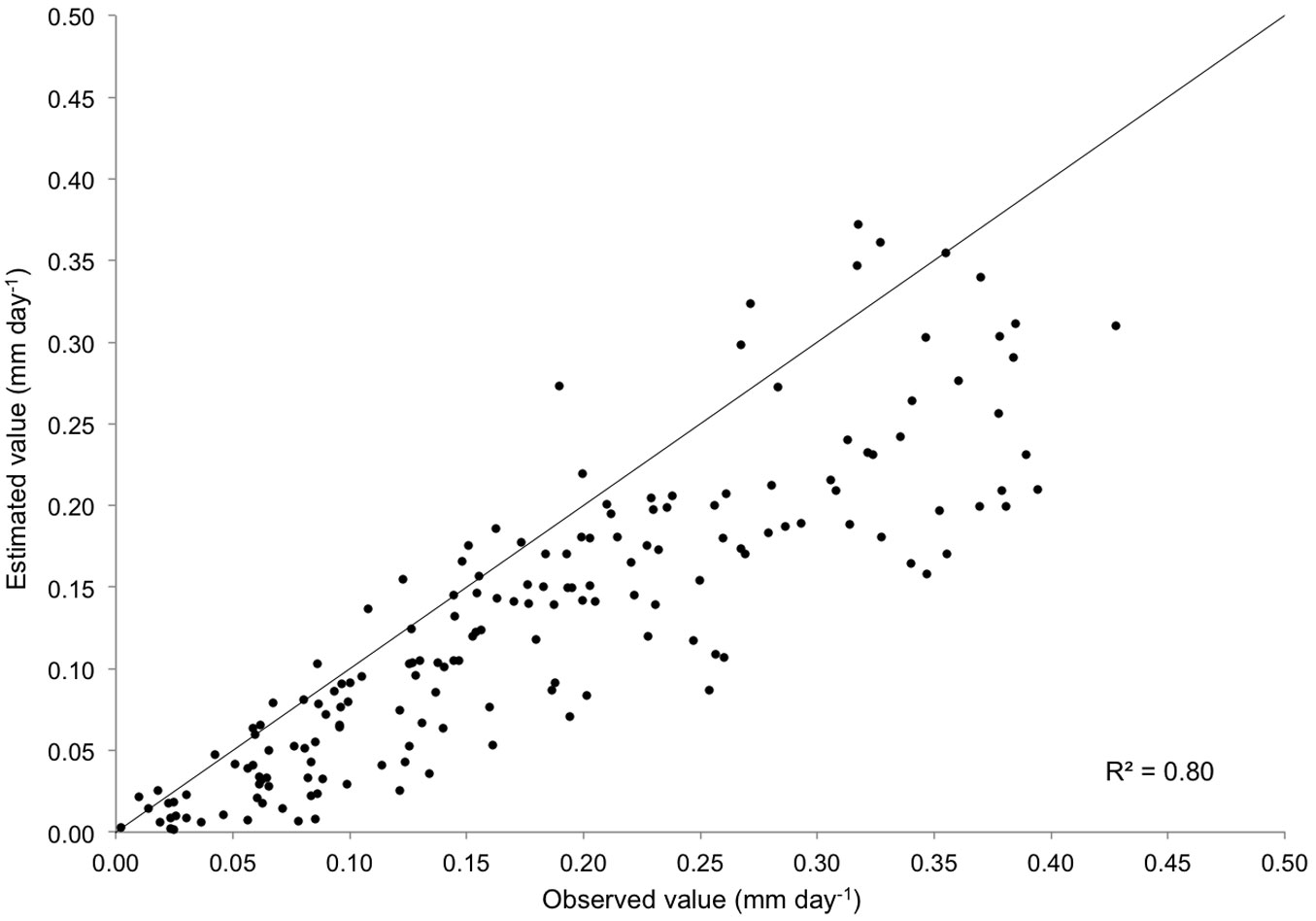
Fig. 3 shows the relationship between the predicted and observed values of stand transpiration. Results were quite accurate, with E values ranging from 0.82 to 0.92. Prediction accuracy did not significantly differ when the network with pooled data was considered (Fig. 3e) or when networks were used separately for each treatment (Fig. 3a-d). Tab. 6 shows the average error obtained in estimating the stand transpiration in different seasons. Significant differences in model performance were detected depending on the season, with the worst results obtained for autumn (Fig. 4). Finally, estimation errors were larger for high values of transpiration, as inferred from the residuals analysis (Fig. 3f).
Fig. 3 - Observed vs. estimated values of stand transpiration by ANN. (a): High intensity thinning treatment; (b): high intensity 1998; (c): low intensity; (d): control; (e): all treatments pooled; (f): residual values for all treatments pooled.
Tab. 6 - Average of observed (Obs) and estimated (Est) stand transpiration (mm day-1) using the Artificial Neural Network per season and treatment. Difference (in mm day-1) represents the average error per season and treatment.
| Season | N | High intensity | High intensity-1998 | Low intensity | Control | Difference | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Obs | Est | Obs | Est | Obs | Est | Obs | Est | |||
| Summer 2009 | 284 | 0.166 | 0.156 | 0.097 | 0.101 | 0.082 | 0.077 | 0.077 | 0.072 | 0.016 |
| Autumn 2009 | 352 | 0.089 | 0.084 | 0.069 | 0.057 | 0.086 | 0.080 | 0.095 | 0.085 | 0.034 |
| Winter 2009-10 | 180 | 0.029 | 0.022 | 0.021 | 0.020 | 0.031 | 0.026 | 0.034 | 0.031 | 0.015 |
| Spring 2010 | 321 | 0.087 | 0.086 | 0.060 | 0.069 | 0.120 | 0.115 | 0.156 | 0.158 | -0.005 |
| Summer 2010 | 300 | 0.164 | 0.169 | 0.028 | 0.027 | 0.174 | 0.168 | 0.202 | 0.209 | -0.005 |
| Autumn 2010 | 273 | 0.094 | 0.100 | - | - | 0.084 | 0.101 | 0.102 | 0.106 | -0.027 |
| Winter 2010-11 | 270 | 0.037 | 0.045 | - | - | 0.052 | 0.060 | 0.066 | 0.071 | -0.021 |
| Spring 2011 | 93 | 0.051 | 0.057 | - | - | 0.067 | 0.070 | 0.091 | 0.093 | -0.011 |
| Difference | - | -0.0020 | 0.0015 | -0.0010 | -0.0022 | -0.0037 | ||||
Fig. 4 - Observed vs. estimated values of stand transpiration by ANN with indication of the season: winter (black squares), spring (purple diamonds), summer (red circles) and autumn (blue triangles).
Use of the PBM Gotilwa+
Gotilwa+ predicted acceptable values of SWC (E from 0.47 to 0.68), though the estimated values for stand transpiration revealed a poor predictive ability of such model, except for the high intensity thinning treatment (E=0.57 - Tab. 7). Comparing ANN and GOTILWA+ performances in terms of stand transpiration, the prediction accuracy achieved with the former model was higher than that obtained with the latter (Tab. 7). The performance of ANN-GOTILWA+ combination was validated comparing measured and estimated transpiration values of control, high, low and high 1998 thinning intensities (Tab. 7). Though the ANN-GOTILWA+ combination performed worse than ANN alone, predicted transpiration values were still accurate (E ranging from 0.52 to 0.77), justifying its further use to estimate stand transpiration when SWC data are not available. Therefore, these results support the use of PBM to feed the ANN as a modeling strategy to estimate the stand transpiration when some of the ANN input data are not readily available. In this sense, ANN-GOTILWA+ was used to predict transpiration values of the medium thinning intensity treatment, where SWC data were not available. The results showed that ANN-GOTILWA+ predicted accurately the stand transpiration, significantly increasing the E value from -6.99 (Gotilwa+) to 0.63 (ANN-GOTILWA+ - Fig. 5, Tab. 7).
Tab. 7 - Comparison between observed and estimated Soil Water Content (SWC) using Process-based Model (GOTILWA+). Observed and estimated transpiration (Tr) using GOTILWA+, the selected Artificial Neural Network (ANN), and the combination ANN-GOTILWA+(SWC). (R): coefficient of correlation; (RMSE): Root Mean Squared Error; (E): Nash-Sutcliffe Efficiency.
| Treatment | Stats | SWC(GOTILWA+) |
Tr(GOTILWA+) |
Tr(ANN) |
Tr(ANN+GOTILWA+) |
|---|---|---|---|---|---|
| High | R | 0.8 | 0.8 | 0.96 | 0.95 |
| RMSE | 0.002 | 0.152 | 0.065 | 0.112 | |
| E | 0.63 | 0.57 | 0.92 | 0.77 | |
| High - 98 | R | 0.70 | 0.73 | 0.91 | 0.91 |
| RMSE | 0.037 | 0.130 | 0.060 | 0.082 | |
| E | 0.47 | 0.19 | 0.82 | 0.68 | |
| Low | R | 0.86 | 0.68 | 0.94 | 0.9 |
| RMSE | 0.036 | 0.427 | 0.081 | 0.124 | |
| E | 0.68 | -2.38 | 0.88 | 0.71 | |
| Control | R | 0.84 | 0.79 | 0.96 | 0.85 |
| RMSE | 0.039 | 0.463 | 0.092 | 0.220 | |
| E | 0.64 | -1.11 | 0.91 | 0.52 | |
| Medium | R | - | 0.87 | - | 0.90 |
| RMSE | - | 0.318 | - | 0.068 | |
| E | - | -6.99 | - | 0.63 |
Fig. 5 - Observed vs. estimated values of stand transpiration in the medium intensity thinning treatment using the parameter soil water content (SWC) generated by the software GOTILWA+.
Discussion
In this study, the influence of adaptative forest management (AFM) on different transpiration modeling approaches in a semiarid pine plantation has been considered. Similarly to Asbjornsen et al. ([3]), the application of a linear approach allowed to identify variables such as SWC, T, Sr, RH and VPD as the inputs that mostly affect the forest transpiration. Such linear approach showed acceptable performance only for some of the treatments considered (Tab. 4). Other studies reported similar R values when predicting transpiration with linear models ([42], [47], [65]). However, we observed that model performance decreases as the forest cover increases (Tab. 4), probably due to the stand competition (canopy closure) as a primary determinant of transpiration over the environmental variables. The inclusion of the forest cover in the grouped linear model clearly worsened its performance. This indicates that even under identical site and climatic conditions, input variables for modeling stand transpiration may be different depending on forest cover, affecting the potential benefits of the model in operational forest management. The common strategy in these cases is the development of specific models in response to threshold behavior of environmental drivers ([42], [48], [65]), like soil moisture or forest cover. Such type of models are applicable only under the specific conditions where they were originally developed.
The artificial neural network modeling approach showed better performance than the two linear models applied (MLR and GLM) in predicting stand transpiration. In particular, neural network modeling showed an improved accuracy in predicting higher values of transpiration, giving high E values (>0.80 - Tab. 5). Nevertheless, prediction accuracy was not the same for all seasons. In particular, the performance of ANN for autumn was not as good as it was for the rest of the year. When larger prediction errors occurred, they could partially be explained by the variability of weather conditions along the day. However, this daily variability was not considered in our model, as only a single daily value was used for each variable. In any case, the relative average error in stand transpiration prediction was quite low, even in autumn (< 11%).
Previous studies have established a relationship between forest transpiration and season, and found differences in the performance of models depending on the season ([25], [11], [59], [17], [70], [16]). Such a different behavior of transpiration is common in geographical regions with marked seasonal variations in the relationships between soil water availability, air temperature, vapor pressure deficit and rain distribution.
The structure of the neural network proposed here is a typical FFNN of three fully connected layers with standard configuration, with only one node in the output layer. Once the input variables are selected, the most relevant decision that determines the dimension or the geometry of the network is the number of hidden nodes (nh) in the hidden or intermediate layer. Optimal network geometry is highly problem-dependent ([49]). We applied a trial-and-error approach, i.e., training a number of different networks with different hidden layer sizes. Best performances were obtained for nh=9, which can be considered a “medium size” network performing adequately and adapted to the problem characteristics. Indeed, such structure has sufficient free weights to capture the essential relationships between variables, but at the same time not too many weights to produce over-fitting of the training data, thus affecting the generalization ability of the network ([41]). Several options were tested for the activation functions representing the individual node’s internal operation. The hyperbolic tangent activation function chosen for the hidden nodes has been applied for similar problems, such as transpiration and trunk sap flow ([50], [47]), with satisfactory results. The most extended option for the output layer is that of linear activation functions ([69], [28]), as it avoids directly the limitation of the range of possible output values. However, in our case the tests carried out with this option yielded a systematic underestimation of the higher values of transpiration. To overcome this problem, the exponential activation function in the output node has been used, producing better stand transpiration predictions, and reducing the observed tendency to underestimate the higher values.
The overall good performance shown by the selected neural network makes such modeling approach a promising tool with several practical implications in forestry. Indeed, the selected model is capable to estimate forest transpiration under different silvicultural treatments, using not only the common meteorological variables and soil water content as inputs, but also the forest cover. In other words, it can successfully be applied to estimate forest transpiration in a wide range of conditions, and can effectively incorporate diverse scenarios including climate change projections. As such, it constitutes a useful modeling support to forest managers for assessing the effect of different thinning intensities on forest transpiration.
GOTILWA+ reproduced accurately the soil water content, while transpiration was systematically underestimated. Some studies compared simulated and measured forest stand transpiration using GOTILWA+ ([39], [52]), but none used direct sap flow measurement in Aleppo pine stands. Kramer et al. ([39]) reported a general systematic discrepancy between observed and predicted stand transpiration using GOTILWA+, with an underestimation particularly relevant at high radiation levels and low temperatures. In the same way, Morales et al. ([52]) applied GOTILWA+ to estimate the actual evapotranspiration of different vegetation types, finding an actual evapotranspiration underestimated by 40-50%. Despite the above discrepancy, the use of GOTILWA+ is still justified, at least in the case when the daily soil water content is not available as input data for ANN models.
Conclusions
In this study, the prediction of stand transpiration based on artificial neural networks gave promising results, to be considered a useful basis for future potential applications in water-oriented forestry and applied hydrology. ANN computational schemes has been successfully applied for the prediction of actual measured transpiration rates of forests from climatic data, soil water content and forest attributes. According to our results, ANN showed an improved capability of transpiration prediction as compared to other linear models. This outcome is consistent with the inherently non-linear relationships associated with the complex physical mechanisms underlying the transpiration process.
The use of prediction methods based on advanced mathematical tools like the ANN can effectively reduce the experimental field work to be held (e.g., sap-flow method) for assessing the stand transpiration, without significantly affecting the overall estimate of the expected transpiration rates, for a given area and a given forest treatment. Furthermore, silvicultural practices (represented in this work by the forest cover variation among treatments) are an input to the neural network, clearly extending the practical benefits of the method. In this sense, forest transpiration can be estimated under a wide range of conditions, for instance, a variety of managing scenarios or even climate change projections. From this perspective, the present approach represents a useful model strategy to provide recommendations for forest management in the light of the forest water use.
Acknowledgements
The authors are grateful to the Valencia Regional Government (CMAAUV, Generalitat Valenciana) and the VAERSA staff for allowing the use of the La Hunde experimental forest and for assistance in carrying out the fieldwork. The authors thank Rafael Herrera and Lelys Bravo de Guenni for their critical reviews of earlier versions of this manuscript. The authors thank Sabina Cerruto Ribeiro for improving the English language. The authors thank the reviewers for their contributions to improve the scientific quality of this paper. TJGF thanks the Mundus 17 program, coordinated by the University of Porto, Portugal.
This study is a part of research projects: “CGL2011-28776-C02-02, HYDROSIL”, “CGL 2014-58127-C3-2, SILWAMED,” funded by the Spanish Ministry of Science and Innovation and FEDER funds, and “Determination of hydrologic and forest recovery factors in Mediterranean forests and their social perception”, led by Dr. Eduardo Rojas and supported by the Ministry of Environment, Rural and Marine Affairs (Spanish Government).
References
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Gscholar
Gscholar
Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
CrossRef | Gscholar
Online | Gscholar
Authors’ Info
Authors’ Affiliation
Antonio D Del Campo
Rafael García-Bartual
María González-Sanchis
Department of Hydraulic Engineering and Environment, Research Group in Forest Science and Technology (Re-ForeST), Universitat Politècnica de València, Camí de Vera s/n, E-46022 Valencia (Spain
Centre of Biological sciences and Nature, Federal University of Acre, Rodovia BR-364, Km 04, Rio Branco, 69915-900 Acre (Brazil)
Corresponding author
Paper Info
Citation
Fernandes TJG, Campo ADD, García-Bartual R, González-Sanchis M (2015). Coupling daily transpiration modelling with forest management in a semiarid pine plantation. iForest 9: 38-48. - doi: 10.3832/ifor1290-008
Academic Editor
Francesco Ripullone
Paper history
Received: Mar 17, 2014
Accepted: Mar 25, 2015
First online: Aug 06, 2015
Publication Date: Feb 21, 2016
Publication Time: 4.47 months
Copyright Information
© SISEF - The Italian Society of Silviculture and Forest Ecology 2015
Open Access
This article is distributed under the terms of the Creative Commons Attribution-Non Commercial 4.0 International (https://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Web Metrics
Breakdown by View Type
Article Usage
Total Article Views: 52022
(from publication date up to now)
Breakdown by View Type
HTML Page Views: 43556
Abstract Page Views: 3245
PDF Downloads: 3838
Citation/Reference Downloads: 26
XML Downloads: 1357
Web Metrics
Days since publication: 3756
Overall contacts: 52022
Avg. contacts per week: 96.95
Article Citations
Article citations are based on data periodically collected from the Clarivate Web of Science web site
(last update: Mar 2025)
Total number of cites (since 2016): 12
Average cites per year: 1.20
Publication Metrics
by Dimensions ©
Articles citing this article
List of the papers citing this article based on CrossRef Cited-by.
Related Contents
iForest Similar Articles
Research Articles
Analyzing regression models and multi-layer artificial neural network models for estimating taper and tree volume in Crimean pine forests
vol. 17, pp. 36-44 (online: 28 February 2024)
Research Articles
Pinus halepensis Mill. in the Mediterranean region: a review of ecological significance, growth patterns, and soil interactions
vol. 18, pp. 30-37 (online: 15 February 2025)
Research Articles
A geographically weighted deep neural network model for research on the spatial distribution of the down dead wood volume in Liangshui National Nature Reserve (China)
vol. 14, pp. 353-361 (online: 27 July 2021)
Review Papers
Should the silviculture of Aleppo pine (Pinus halepensis Mill.) stands in northern Africa be oriented towards wood or seed and cone production? Diagnosis and current potentiality
vol. 12, pp. 297-305 (online: 27 May 2019)
Research Articles
Artificial intelligence associated with satellite data in predicting energy potential in the Brazilian savanna woodland area
vol. 13, pp. 48-55 (online: 05 February 2020)
Research Articles
Identification of wood from the Amazon by characteristics of Haralick and Neural Network: image segmentation and polishing of the surface
vol. 15, pp. 234-239 (online: 14 July 2022)
Research Articles
Yield of forests in Ankara Regional Directory of Forestry in Turkey: comparison of regression and artificial neural network models based on statistical and biological behaviors
vol. 16, pp. 30-37 (online: 22 January 2023)
Research Articles
Comparison of alternative harvesting systems for selective thinning in a Mediterranean pine afforestation (Pinus halepensis Mill.) for bioenergy use
vol. 14, pp. 465-472 (online: 16 October 2021)
Review Papers
Biomass, radial growth and regeneration capacity of Aleppo pine, and its possible use as rootstock in arid and degraded areas
vol. 15, pp. 213-219 (online: 16 June 2022)
Research Articles
Controlled-release fertilizers combined with Pseudomonas fluorescens rhizobacteria inoculum improve growth in Pinus halepensis seedlings
vol. 8, pp. 12-18 (online: 12 May 2014)
iForest Database Search
Search By Author
Search By Keyword
Google Scholar Search
Citing Articles
Search By Author
Search By Keywords
PubMed Search
Search By Author
Search By Keyword